カプランマイヤー法による生存時間推定について
記事の目次
Toggleはじめに
生存時間解析(Survival Analysis)は、イベント発生までの時間を扱う統計手法です。
製薬業界では、以下のようなエンドポイントで頻繁に用いられます。
- OS(Overall Survival):全生存期間
- PFS(Progression-Free Survival):無増悪生存期間
- TTP(Time to Progression):進行までの時間
- TTF(Time to Treatment Failure):治療失敗までの時間
これらは打ち切り(Censoring)を含むことが多く、単純な平均値では正しく評価できません。そこで登場するのがカプランマイヤー法(Kaplan–Meier法)です。今回はカプランマイヤー法について紹介していこうと思います。
生存時間解析の導入と基礎概念については下記で記事を記載しておりますので、興味がある方は是非ご一読ください。

経験生存関数について
時刻t以上で被験者が生存する確率の推定値は以下のように与えることができる。
\[\tilde{S}(t)=\frac{生存時間がt以上となる被験者数}{全被験者数}\]
上記関数を計算する方法として、カプランマイヤー法があります。
カプランマイヤー法の定義と数式
カプランマイヤー推定量は以下で表されます。
\[\hat{S}(t) = \prod_{i=1}^{s} \left( 1 – \frac{d_i}{n_i} \right)\]
- n_i:時刻 t_i 直前のリスク集合の人数
- t_i:i番目のイベント発生時刻
- d_i:時刻 t_i におけるイベント数
ここからは、カプランマイヤー推定量を導出していきたいと思います。数式が多く出てきますが、考え方や導出を一度でも見ておくことで統計検定でも活用できます。
以下のような状況を考えます。
- \(t_{i}\):イベント発生時点
- \(d_{i}\):死亡数
- \(u_{i}\):打ち切り数
このとき\(t_{1} < t_{2} < … < t_{r}\)の下で\(t_{s} \le t < t_{s+1}\)に対するカプランマイヤー推定法を求めていく。
$$
\begin{eqnarray}
S(t) &=& P(T > t) \\
&=& P(T > t , T > t_{s}) \\
&=& P(T > t_{s})P(T > t | T > t_{s}) \\
&=& P(T > t_{s} , T > t_{s-1})P(T > t | T > t_{s}) \\
&=& P(T > t_{s-1})P(T > t | T > t_{s-1})P(T > t | T > t_{s}) \\
&=& \vdots \\
&=& P(T > t_{1})P(T > t_{2} | T > t_{1}) \cdots P(T > t | T > t_{s-1})P(T > t | T > t_{s})
\end{eqnarray}
$$
ここで、
$$
\begin{eqnarray}
P(T > t_{1}) &=& P(T > t_{1} , T > t_{0}) \\
&=& P(T > t_{0})P(T > t_{1} | T > t_{0}) \\
&=& P(T > t_{1})P(T > t_{0}) \\
&=& 1 – P(T \le t_{1} | T > t_{0})
\end{eqnarray}
$$
これにより、
$$
\begin{eqnarray}
S(t) &=& P(T > t_{1} | T > t_{0})P(T > t_{2} | T > t_{1}) \cdots P(T > t | T > t_{s-1})P(T > t | T > t_{s})\\
&=& (1 – P(T \le t_{1} | T > t_{0}))(1 – P(T \le t_{2} | T > t_{1})) \cdots (1 – P(T \le t | T > t_{s}))\\
&=& \prod_{i=1}^{s}(1 – P(T \le t_{i} | T > t_{i-1}))(1 – P(T \le t | T > t_{s}))
\end{eqnarray}
$$
ここで、\(P(T \le t_{s} | T > t_{s}) = 0 \)であり、\(T = t_{1},t_{2},…,t_{r}\)の値しかとらないため、離散データである。よって、 \(P(T \le t_{i} | T > t_{i-1})=P(T = t_{i} | T > t_{i-1})\)とすると、
$$
\begin{eqnarray}
S(t) &=& \prod_{i=1}^{s}(1 – P(T \le t_{i} | T > t_{i-1}))(1 – P(T \le t | T > t_{s}))
&=& \prod_{i=1}^{s}(1 – \lambda_{i})
\end{eqnarray}
$$
ここで、推定値を考えていくと、
\[\hat{\lambda_{i}} = \hat{P}(T \le t_{i} | T > t_{i-1}) = \frac{d_{i}}{n} \]
ここで、\(n_{i}\)は\(t_{i}\)時点のリスクセットのサイズで\(n_{i} = n – (d_{1} + \cdots + d_{i-1}) – (u_{0} + \cdots + u_{i-1})\)である。
そのため、カプランマイヤー推定値は、
\[\hat{S}(t) = \prod_{i=1}^{s}(1 – \frac{d_{i}}{n_{i}})\]
また生存関数の標準誤差や信頼区間も求めることが可能です。導出方法については別の記事で紹介していますので、結果のみ示しておきます。
標準誤差:
\[SE(\hat{S}(t)) \approx \hat{S}(t)\sqrt{\sum_{i=1}^{r}\frac{d_{i}}{n_{i}(n_{i}-d_{i})}}\]
信頼区間:
\[g^{-1}(g(\hat{S}(t)) \pm 1.96SE[g(\hat{S}(t))])\]
ここで、\(g(\hat{S}(t))= log(-log\hat{S}(t))\)

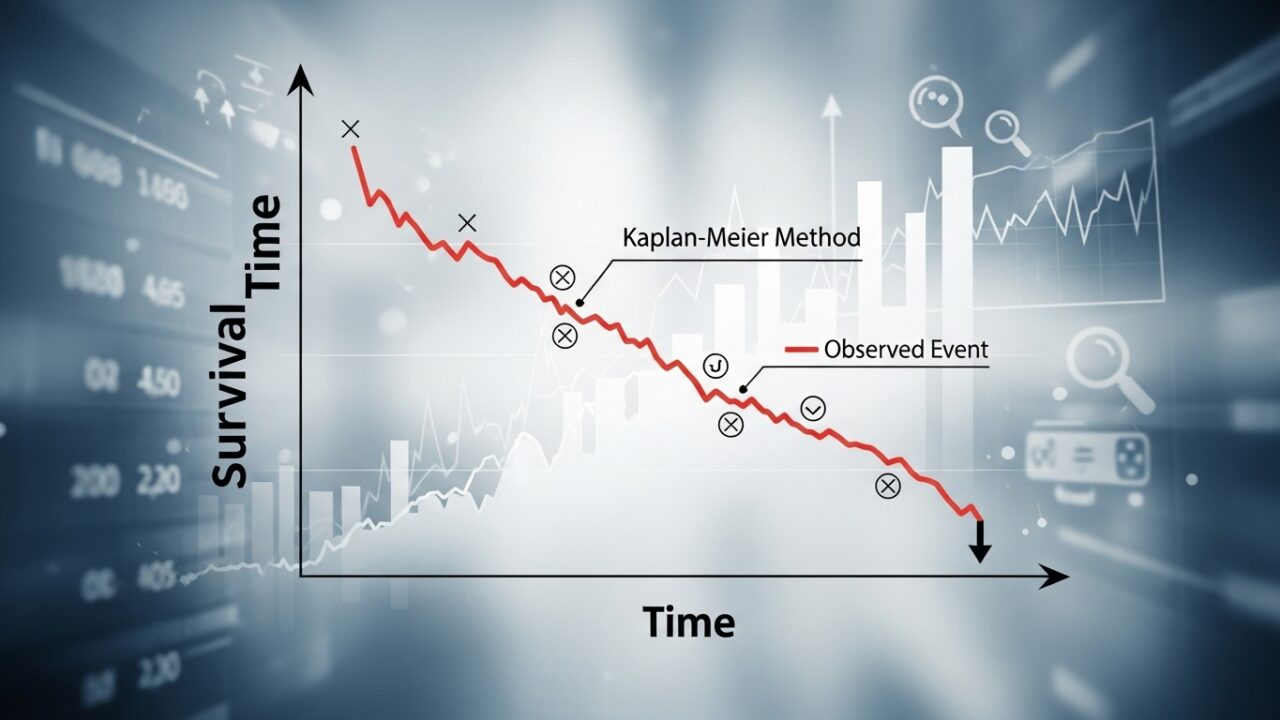
カプランマイヤー曲線の図解
出力されたカプランマイヤー曲線は下記のようになります。
- 階段が落ちる:イベント発生
- ヒゲ:打ち切り
- Number at risk : リスク(死亡等)が発生する可能性がある数、つまり時間が経過するにつれてイベントや打ち切りにより減っていく。
Rによる実装例
#必要パッケージ
library(survival)
library(survminer)
set.seed(123) # 再現性確保
#==== ダミーデータ作成 ====
n <- 50 # 被験者数
trial_data <- data.frame(
time = round(rexp(n, rate = 0.1), 1), # 生存時間(指数分布から生成)
status = sample(c(1, 0), n, replace = TRUE, # 1=イベント発生, 0=打ち切り
prob = c(0.7, 0.3)),
group = sample(c(“Treatment”, “Control”), # 群割付
n, replace = TRUE)
)
#==== KM推定 ====
fit <- survfit(Surv(time, status) ~ group, data = trial_data)
#==== KM曲線描画 ====
ggsurvplot(
fit,
data = trial_data,
risk.table = TRUE, # Number at risk 表示
conf.int = TRUE, # 信頼区間
pval = TRUE, # p値(ログランク検定)
censor.shape = 124, # 打ち切りマーク
censor.size = 3,
xlab = “Time (months)”,
ylab = “Survival probability”,
break.time.by = 5, # x軸目盛
risk.table.height = 0.25,
ggtheme = theme_minimal()
)
実務での留意点
打ち切りの扱い
- 治験中止・追跡不能・試験終了時点で生存 → 打ち切り
- 打ち切りは欠測ではなく「少なくともその時点まではイベントなし」という情報
規制当局(PMDA, FDA, EMA)での要求
- KM曲線にはNumber at riskを明示
- 中央生存期間(Median Survival Time, MST)と95%信頼区間を併記
- 群間比較にはログランク検定やCox比例ハザードモデルを併用
まとめ
カプランマイヤー法は打ち切りを考慮した生存率推定の標準手法となります。製薬業界では規制当局向け報告や論文投稿で使われる機会が多くあるかと思います。実務ではNumber at riskや信頼区間の明示をすることにより、視覚的にも分かりやすく解釈することが可能です。群間比較や共変量調整にはKM法単独でなくCox回帰等と併用することでより科学的な議論を行えるかと思います。