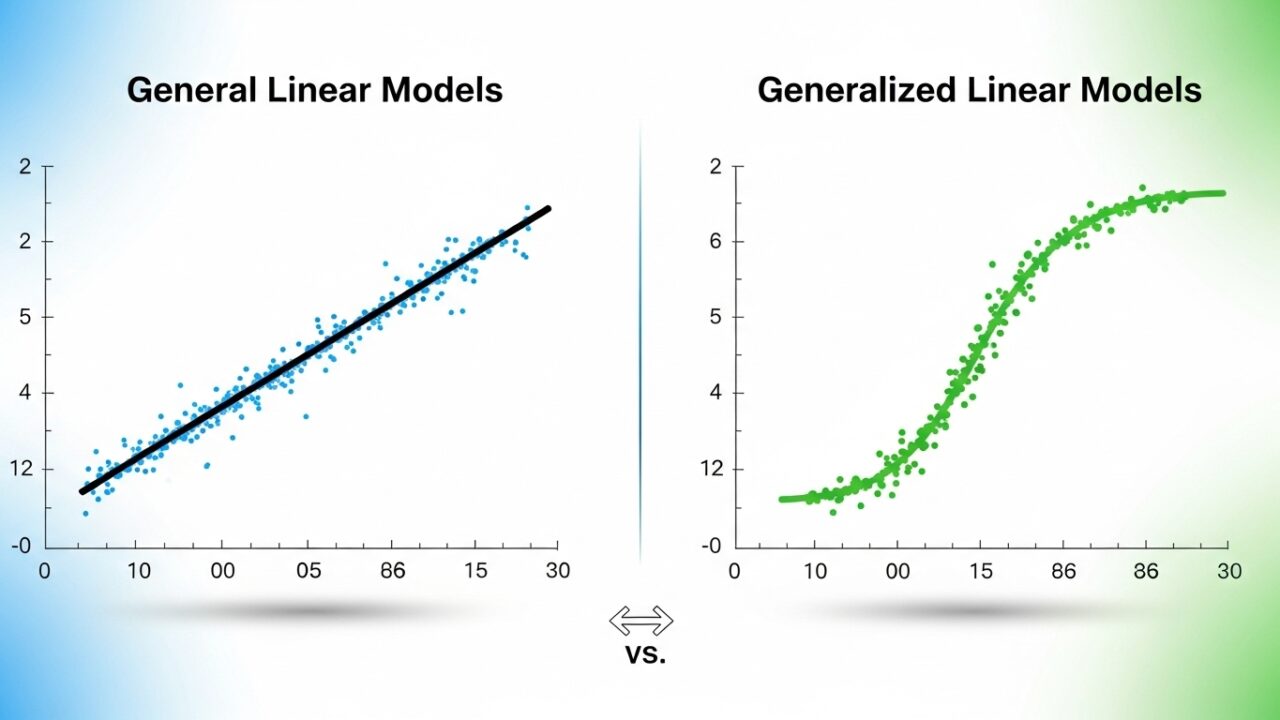
一般線形モデルと一般化線形モデルの違いを徹底解説
記事の目次
Toggleはじめに
統計解析の現場では、説明変数と目的変数の関係を明らかにするために「回帰モデル」が多用されます。その中でも、一般線形モデル(General Linear Model: 以下、線形モデル) と 一般化線形モデル(Generalized Linear Model: 以下、一般化線形モデル) は、解析の基礎をなす重要な枠組みです。統計検定でもこの2つの統計解析手法の理解が求められます。
名前が似ているため混同されがちですが、扱えるデータの種類や分布、適用範囲において大きな差があります。本稿では両者の仕組みと違いを、数式・図解・比較表を用いてわかりやすく解説します。
一般線形モデルとは
一般線形モデルは、目的変数が正規分布に従う連続値データに対して使うモデルです。
以下の条件を満たすものとなっております。
- 応答変数Yが正規分布に従う
- Yの平均をパラメータの一次結合で表すことができる、すなわち直線的な関係を持っていること
\[\mathbf{y} = \mathbf{X}\boldsymbol{\beta} + \boldsymbol{\varepsilon}, \quad \boldsymbol{\varepsilon} \sim N(\mathbf{0}, \sigma^2\mathbf{I})\]
- \(\boldsymbol{\varepsilon}:誤差項(平均0、分散\sigma^2の正規分布)\)
- \(\mathbf{y}:目的変数(n×1)\)
- \(\mathbf{X}:説明変数(n×pのデザイン行列)\)
- \(\boldsymbol{\beta}:回帰係数\)
- 誤差項は 正規分布
- 恒等リンク関数\((g(\mu)=\mu)\)のみ
- 推定法は最小二乗法
- 用途:連続値データの予測や効果検証
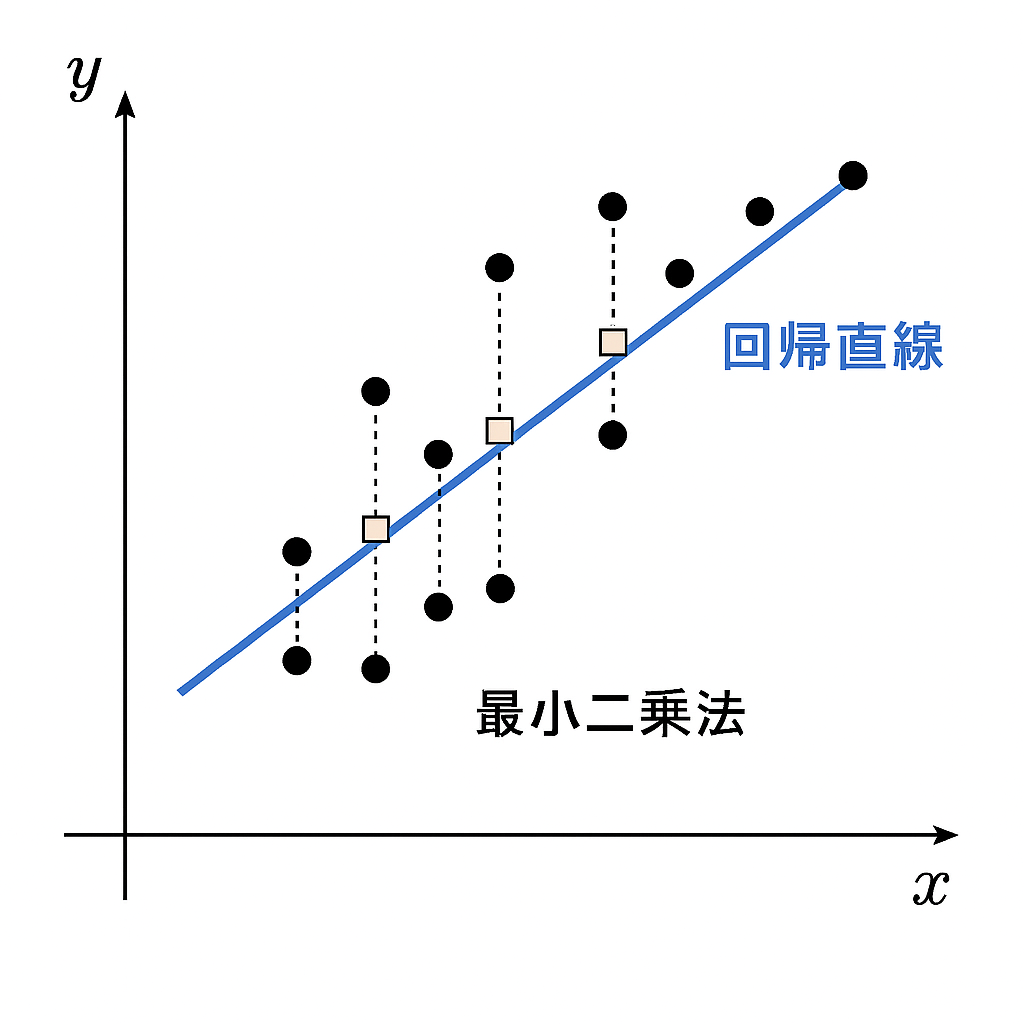
最小二乗法について
各観測値 \(y_i\) と予測値 \(\hat{y}_i\) の差(残差)を二乗し、それらをすべて足し合わせたものです。最小二乗法では、この合計値が最も小さくなるように回帰直線を決定します。
\[\sum_{i=1}^{n}(y_i – \hat{y}_i)^2\]
一般線形モデルの例として、単回帰・重回帰、分散分析(ANOVA)、共分散分析(ANCOVA)があります。
一般化線形モデルとは
登場の背景
現実のデータは、必ずしも連続値・正規分布とは限りません。例えば:
- 成功/失敗の二値(例:臨床試験の有効性判定)
- カウントデータ(例:交通事故件数)
- 正の連続値(例:医療費)
こうしたデータに対応するため、分布や関数を柔軟に選べる一般化線形モデルが登場しました。以下の2つの条件を満たし、式で表すと下記のようになります。
- 応答変数Yが指数型分布族に従う
- Yの平均をある関数で変化させたとき、パラメータの一次結合で表すことができる
\[g(\mu_i) = \mathbf{x}_i^\top\boldsymbol{\beta}\]
- \(\mu_i = E[Y_i]:目的変数の期待値\)
- \(g(\cdot)\):リンク関数
- 誤差分布:指数型分布族(正規、二項、ポアソン、ガンマ等)
- 分布の選択肢が豊富(正規・二項・ポアソン・ガンマ…)
- リンク関数で非線形関係を線形化
- 推定には 最尤推定法(MLE) を使用
- 線形モデルを特別なケースとして内包
| モデル名 | 応答変数の分布 | リンク関数 | 主な用途 | グラフの概形 |
| 正規分布(一般線形モデル) | 正規分布 | 恒等関数\((\mu)\) | 連続値の予測(身長、体重など) | 散布図+回帰直線 |
| ロジスティック回帰 | 二項分布 | \(logit(\log\frac{\mu}{1-\mu})\) | 成功/失敗、Yes/Noなどの二値データ | S字カーブ(確率0〜1) |
| ポアソン回帰 | ポアソン分布 | 対数\((\log\mu)\) | カウントデータ(事故件数、来店数など) | 右に裾の長い棒グラフ |
| ガンマ回帰 | ガンマ分布 | inverse\((1/\mu)やlog\) | 正の連続値(医療費、待ち時間など) | 右裾の長い連続分布 |
単一のパラメータ\(\theta \)をもつ確率分布に従う確率変数Yに対してその確率分布が以下の式で表現することができるとき、その分布は指数型分布族に属する。
\[f(y;\theta)=\exp(a(y)b(\theta)+c(\theta)+d(y))\]
両者の違いまとめ
| 観点 | 一般線形モデル | 一般化線形モデル |
| 分布 | 正規のみ | 指数型分布族 |
| 応答変数 | 連続値のみ | 連続・離散・カテゴリ |
| リンク関数 | 恒等のみ | 任意(logit, log, identity…) |
| 推定法 | 最小二乗法 | 最尤推定法 |
| 主な用途 | 回帰・分散分析 | ロジスティック、ポアソン、ガンマ回帰など |
実務での選び方
基本的には以下の場合を仮定できるときに選んでいけばよいと思います。
- 連続値+正規近似可 → 一般線形モデル
- 二値・カウント・非正規 → 一般化線形モデル
💡 例:臨床試験では、血圧変化量はANCOVA(線形モデル)、有害事象発生有無はロジスティック回帰(一般化線形モデル)を使い分ける
ケーススタディ
ケース1:薬剤効果の解析(連続アウトカム)
シナリオ:新薬Aとプラセボの2群で、治療前後の血圧変化量(mmHg)を比較。治療前の血圧を共変量として調整。
- アウトカム:治療前後の血圧変化量(mmHg)
- モデル:ANCOVA(一般線形モデル)
- 理由:連続値+正規性が概ね担保される
モデル式
\[\text{ChangeBP}_i = \beta_0 + \beta_1 \times \text{Group}_i + \beta_2 \times \text{BaselineBP}_i + \varepsilon_i \]
データ例
df <- data.frame(
ChangeBP = c(-5, -3, -8, -2, -6, -4, -1, -7),
Group = factor(c(“DrugA”, “DrugA”, “DrugA”, “DrugA”,
“Placebo”, “Placebo”, “Placebo”, “Placebo”)),
BaselineBP = c(150, 148, 152, 149, 151, 150, 153, 149)
)
ANCOVAモデル
fit <- lm(ChangeBP ~ Group + BaselineBP, data = df)
summary(fit)
ケース2:副作用発生有無の解析(二値アウトカム)
シナリオ:有害事象(AE)の発生有無を予測。説明変数は治療群と年齢。
- アウトカム:有害事象の有無(Yes/No)
- モデル:ロジスティック回帰(一般化線形モデル)
- 理由:二値データで正規分布を仮定できない
モデル式
\[\log\frac{p_i}{1-p_i} = \beta_0 + \beta_1 \cdot \text{Group}_i + \beta_2 \cdot \text{Age}_i \]
データ例
df <- data.frame(
AE = c(1, 0, 1, 0, 0, 1, 0, 0),
Group = factor(c(“DrugA”, “DrugA”, “DrugA”, “DrugA”,
“Placebo”, “Placebo”, “Placebo”, “Placebo”)),
Age = c(65, 59, 72, 68, 70, 66, 60, 64)
)
ロジスティック回帰
fit <- glm(AE ~ Group + Age, data = df, family = binomial(link = “logit”))
summary(fit)
オッズ比と95%信頼区間
exp(cbind(OR = coef(fit), confint(fit)))
まとめ
今回は一般線形モデルと一般化線形モデルの違いについてそれぞれ解説いたしました。それぞれの主な特徴として一般線形モデルは、単純で解釈しやすいが適用範囲は狭い、一般化線形モデルは、リンク関数と分布を柔軟に選べる拡張型となります。
どちらを選ぶか検討していく際には、データの型と分布特性に応じてモデルを選ぶことが重要となります。

![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/4aa03195.892069bb.4aa03196.39df6be9/?me_id=1213310&item_id=13039446&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F8679%2F9784320018679_1_2.jpg%3F_ex%3D300x300&s=300x300&t=picttext)