第6回 傾向スコア分析を用いた交絡調整 ― 製薬業界における実務応用とRによる実装
記事の目次
Toggleはじめに
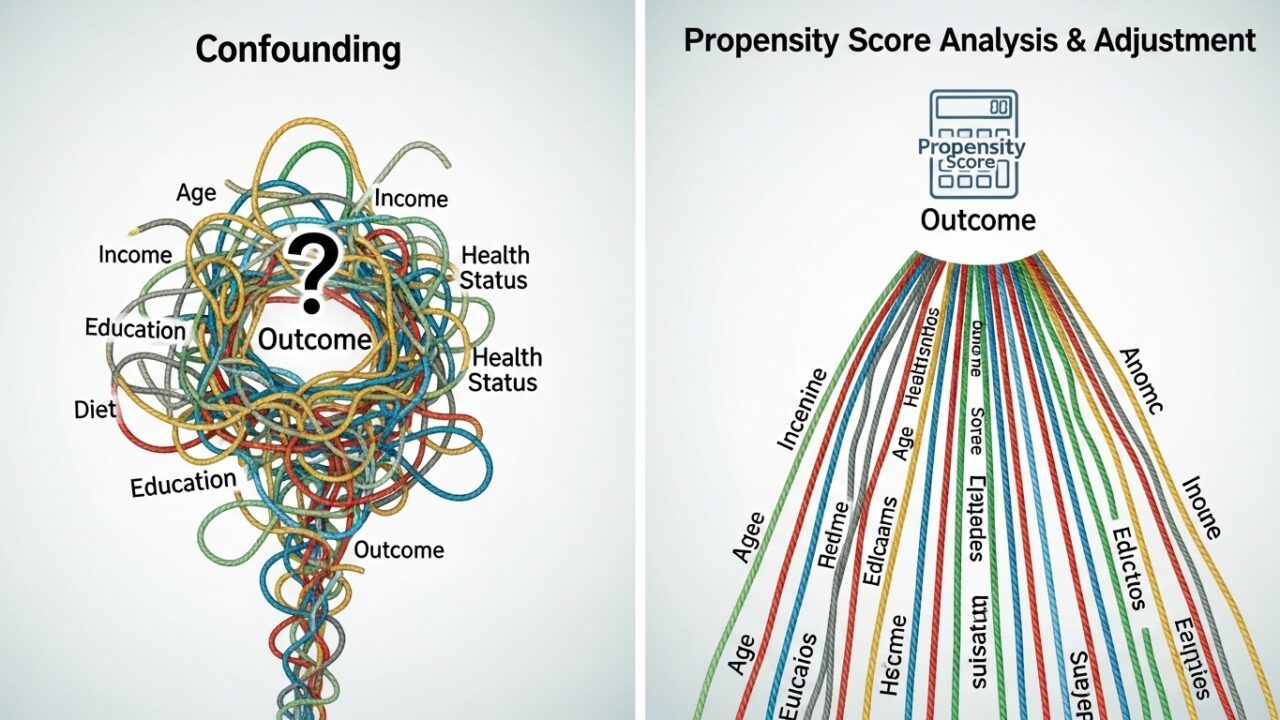
製薬業界において、臨床研究や疫学研究は新薬の有効性や安全性を評価する上で不可欠です。しかし、現実のデータを用いた観察研究では、交絡因子(confounder)の存在が因果推論を難しくします。例えば、新薬を服用する患者群と従来薬を服用する患者群を比較する際、年齢や併存疾患といった背景因子が治療選択に影響し、結果の解釈を歪める可能性があります。
この問題を克服するために用いられる代表的な手法が傾向スコア分析(Propensity Score Analysis)です。本記事では、製薬業界での実務応用を意識しながら、傾向スコアの基本概念からRによる実装例までを解説します。
傾向スコアとは何か?
傾向スコアとは、「ある患者が特定の治療を受ける確率を、観測可能な背景因子に基づいて推定した値」です。
例えば、新薬Aと従来薬Bを比較する研究で、患者の年齢・性別・併存疾患・既往歴などを説明変数とし、治療選択(AかBか)を目的変数としたロジスティック回帰モデルを構築します。その予測確率が傾向スコアです。
傾向スコアを用いることで、治療群と対照群の背景因子を統計的にバランスさせ、「あたかもランダム化比較試験(RCT)」のような比較を可能にします。
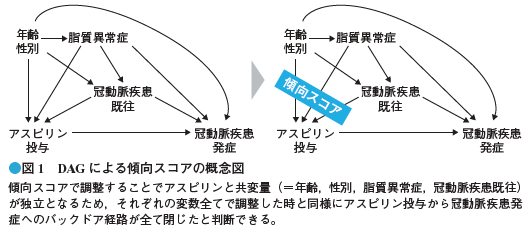
傾向スコアをどのように使うかを具体例を用いて説明していきます。具体例としてアスピリン投与(X)が冠動脈疾患発症(Y)を予防する効果について考えてみます。下記DAGが示すようにアスピリンと冠動脈疾患には多くの交絡因子(Z)が存在します。
これらの交絡因子を用いてアスピリンの傾向スコア を算出し,Y に対する(例えば)ロジス
ティック回帰モデル \(log〔P(Y=1)/{1-P(Y=1)}〕=\alpha + \beta_{x} X+\beta_{PS} PS \) を当てはめます。するとアスピリン投与から冠動脈疾患発症に向かうバックドア経路が,PS の調整で(曝露と共変量が独立となるため)全て閉じたと判断で
き、アスピリン投与による因果効果を\(\beta_{x}\)として求められます。
https://www.igaku-shoin.co.jp/paper/archive/y2021/3435_05
傾向スコア分析の代表的な方法
傾向スコアを用いた交絡調整には複数のアプローチがあります。
- マッチング(Matching)
治療群と対照群で傾向スコアが近い患者をペアにして比較する。 - 層別化(Stratification)
傾向スコアを分位点で区切り、層ごとに治療効果を推定する。 - 重み付け(IPTW: Inverse Probability of Treatment Weighting)
傾向スコアの逆数を重みとして解析することで、仮想的にバランスの取れた母集団を作る。 - 共変量調整(Covariate Adjustment)
傾向スコアを共変量として回帰モデルに組み込む。
製薬業界の実務では、マッチングとIPTWが特に多用されます。理由は、直感的に理解しやすく、規制当局への説明責任を果たしやすいからです。
実務での応用シナリオ
製薬企業での典型的な応用例を挙げます。
希少疾患領域
RCTが困難な場合に、観察研究で因果推論を補強する。
市販後調査(PMS)
新薬と既存薬の安全性比較において、患者背景の違いを補正する。
リアルワールドデータ(RWD)解析
レセプトデータや電子カルテデータを用いた有効性評価で、交絡を調整する。
Rによる実装例
ここでは、仮想データを用いて「新薬A vs 従来薬Bの心血管イベント発症リスク」を比較する例を示します。
# 仮想データの生成
set.seed(123)
n <- 1000
age <- rnorm(n, 65, 10)
sex <- rbinom(n, 1, 0.5)
comorbidity <- rbinom(n, 1, 0.3)
treatment <- rbinom(n, 1, plogis(-3 + 0.05age + 0.8comorbidity))
outcome <- rbinom(n, 1, plogis(-2 + 0.03age + 0.5treatment))
data <- data.frame(age, sex, comorbidity, treatment, outcome)
# ロジスティック回帰で傾向スコアを推定
ps_model <- glm(treatment ~ age + sex + comorbidity,
family = binomial(), data = data)
data$ps <- predict(ps_model, type = “response”)
解釈
- 年齢や併存疾患があるほど「新薬を選択する確率(傾向スコア)」が高いことが確認できます。
- これは臨床現場で「リスクの高い患者に新薬が投与されやすい」傾向を反映しています。
library(MatchIt)
# 1対1最近傍マッチング
m.out <- matchit(treatment ~ age + sex + comorbidity,
data = data, method = “nearest”, ratio = 1)
matched_data <- match.data(m.out)
# マッチング後のバランス確認
library(cobalt)
love.plot(m.out, binary = “std”)
解釈
- Love plotで標準化差分(Standardized Mean Difference, SMD)を確認します。
- マッチング前は「年齢」「併存疾患」で治療群と対照群に差がありましたが、マッチング後はSMDが0.1未満に収まり、背景因子のバランスが改善されたことがわかります。
# マッチング後データで治療効果を推定
glm_out <- glm(outcome ~ treatment, family = binomial(),
data = matched_data)
summary(glm_out)
解釈(例)
- 回帰係数(treatmentのオッズ比)が 1.6(95%CI: 1.1–2.3, p=0.02) と仮定します。
- これは「新薬群は従来薬群に比べて心血管イベントの発症リスクが約1.6倍高い」と解釈できます。
- ただし、これはあくまで観察研究に基づく推定であり、未測定交絡の可能性は残ります。
実務での注意点
製薬業界で傾向スコア分析を応用する際には、以下の点に注意が必要です。
感度分析
マッチングとIPTWを併用し、結果の一貫性を確認することが望ましいです。
交絡因子の網羅性
傾向スコアは「観測可能な交絡因子」に基づくため、未測定交絡は補正できません。
モデルの適合性
傾向スコア推定モデルの仕様(変数選択、非線形項、交互作用)に依存します。
規制当局への説明
FDAやPMDA等に提出する解析では、手法の妥当性と透明性が求められます。
まとめ
今回は、傾向スコアの基本概念からRによる実装例までを解説しました。傾向スコア分析は、観察研究における交絡調整の強力なツールであり、製薬業界の実務においても広く活用されています。RCTが困難な状況でも、適切に設計・実装すれば、臨床的に意味のある因果推論を可能にします。
R言語を用いれば、傾向スコアの推定からマッチング・重み付け・解析まで一貫して実施でき、再現性の高い研究が可能です。今後、リアルワールドデータの活用が進む中で、傾向スコア分析はますます重要性を増していくでしょう。