第5回 多変量回帰モデルを因果推論に用いる――製薬業界で働く人のための実践的ガイド
記事の目次
Toggleはじめに
製薬企業における臨床研究や疫学研究では、「ある治療や曝露がアウトカムにどのような因果効果を持つのか」を明らかにすることが重要です。新薬の有効性評価、安全性シグナルの探索、リアルワールドデータを用いた薬剤疫学研究など、日常的に因果推論の考え方が求められます。
その中で最も広く使われている統計手法の一つが多変量回帰モデルです。回帰モデルは単なる「予測ツール」として理解されがちですが、適切に設計・解釈すれば因果推論の強力な道具となります。本稿では、多変量回帰モデルを因果推論に活用する際の考え方、注意点、そして実務での実装例をRコードとともに解説します。
多変量回帰モデルと因果推論の関係
回帰モデルの基本
多変量回帰モデルは、アウトカム Y を曝露 X と共変量 Z の関数として表現します。
\[Y = \beta_0 + \beta_1 X + \beta_2 Z_1 + \beta_3 Z_2 + \cdots + \varepsilon\]
ここで \(\beta_1\) は「曝露 X がアウトカム Y に与える効果」を表す係数です。
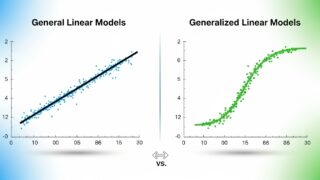
以下には代表的な一般化線形モデル(GLM)の種類と\(\beta_x\)の解釈を表で表しておきます。
| GLMモデル | 目的変数の型 | リンク関数R(Y) | 分布族(family) | \(\beta_x\)の解釈(\(Z_1,Z_2,…\)という条件付き) |
| 線形回帰モデル | 連続変数 | Y | 正規分布 | X の1 単位増加は,平均してY のβ単位増加と 関連がある |
| ロジスティック回帰モデル | 2値変数 | log[{P(Y)}/11-P(Y)] | 二項分布 | X の1 単位増加は,平均してY のオッズが\(e^{β_{x}}\)倍になることと関連がある(\(e^{β_{x}}\):オッズ比) |
| 修正ポアソン回帰モデル | 2値変数 | log{P(Y)} | ポアソン分布 | X の1 単位増加は,平均してY のリスクが\(e^{β_{x}}\)倍になることと関連がある(\(e^{β_{x}}\):リスク比) |
因果推論との違い
単純に回帰を当てはめただけでは、\(\beta_1\) が因果効果を意味するとは限りません。なぜなら、交絡因子が存在するからです。交絡因子とは、曝露とアウトカムの両方に影響を与える変数であり、これを適切に調整しないと「見かけの関連」を因果効果と誤解してしまいます。
製薬企業で直面する典型的なシナリオ
新薬の有効性評価
例えば「新薬Aが心血管イベントを減らすか」を観察研究で評価する場合、患者背景(年齢、性別、併存疾患、生活習慣など)が交絡因子となります。
安全性シグナルの探索
薬剤Bと肝障害の関連を調べる際、アルコール摂取や既往歴が交絡因子となり得ます。
リアルワールドデータ解析
電子カルテや保険データを用いた解析では、交絡因子の網羅性が課題となり、回帰モデルでの調整が重要になります。
因果推論における多変量回帰の位置づけ
因果推論では、まずDAG(Directed Acyclic Graph)を描き、曝露・アウトカム・交絡因子の関係を整理します。
例:薬剤使用(X)→ 心血管イベント(Y)
交絡因子:年齢(Z1)、喫煙(Z2)
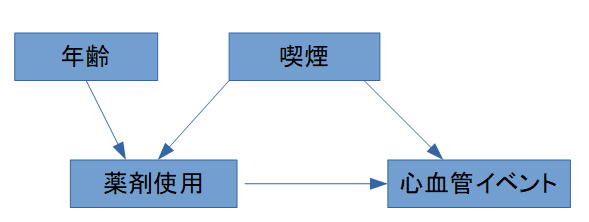
この場合、年齢と喫煙を調整することで、薬剤使用の因果効果を推定できる可能性があります。
多変量回帰モデルの実装例
ここでは、架空データを用いて「薬剤使用が心血管イベントに与える影響」を評価する例を示します。
# データ例
set.seed(123)
n <- 1000
age <- rnorm(n, mean=65, sd=10)
smoking <- rbinom(n, 1, 0.3)
drug <- rbinom(n, 1, plogis(-3 + 0.04age + 0.8smoking))
event <- rbinom(n, 1, plogis(-5 + 0.05age + 0.6smoking + 0.5*drug))
data <- data.frame(age, smoking, drug, event)
# ロジスティック回帰
model <- glm(event ~ drug + age + smoking, data=data, family=binomial)
summary(model)
# オッズ比を計算
exp(coef(model))
出力の解釈
drugの係数が薬剤使用の効果を表す。exp(coef(model))によりオッズ比を算出できる。- 交絡因子(年齢・喫煙)を調整しているため、薬剤使用の効果をより因果的に解釈できる。
因果推論における注意点
過剰調整
中間因子(曝露の結果として生じる変数)を調整すると、因果効果を過小評価する可能性があります。
未測定交絡
測定できない交絡因子がある場合、回帰モデルだけでは因果推論は不完全です。感度分析や傾向スコア法などの補完的手法が必要です。
モデルの適合性
線形性の仮定や交互作用の有無を確認することも重要です。
製薬企業での実務的活用
マーケットアクセス:保険償還申請時に、観察研究のエビデンスを補強。
臨床開発:治験外のリアルワールドデータを補完的に解析し、薬剤の有効性・安全性を検証。
薬剤疫学:市販後調査での副作用リスク評価に活用。
まとめ
今回は多変量回帰モデルを因果推論に活用する際の考え方を中心に解説いたしました。多変量回帰モデルは、製薬企業における臨床研究や疫学研究で最も広く使われる統計手法の一つです。単なる予測モデルとしてではなく、交絡因子を適切に調整することで因果推論の道具として活用できる点が重要です。
因果推論の観点からは、まず DAG(因果ダイアグラム) を用いて曝露・アウトカム・交絡因子の関係を整理し、どの変数を調整すべきかを明確にします。その上で多変量回帰モデルを構築することで、観察研究においても「仮想的な介入」を再現し、因果効果を推定することが可能となります。
実務上は、
- 新薬の有効性評価
- 副作用リスクの探索
- リアルワールドデータ解析
といった場面で多変量回帰が活用されます。R言語を用いれば、ロジスティック回帰などを通じて曝露の効果をオッズ比として推定でき、臨床的に解釈可能な形で結果を提示できます。ただし、過剰調整(中間因子の調整)や未測定交絡といった限界には注意が必要です。回帰モデルだけで因果推論が完全に成立するわけではなく、傾向スコア法や感度分析など補完的手法と組み合わせることが望まれます。
総じて、多変量回帰モデルは「因果推論の第一歩」として非常に有用です。適切な設計と解釈を行えば、製薬企業の研究現場においても、より信頼性の高いエビデンスを創出し、臨床や規制の意思決定に貢献できるでしょう。