第4回 層別解析により因果効果を推定する――製薬業界で働く人のための実践的ガイド
記事の目次
Toggleはじめに
製薬業界における臨床研究や疫学研究では、因果効果を正しく推定することが常に求められます。新薬の有効性評価、副作用リスクの検証、市販後調査(PMS)、リアルワールドエビデンス(RWE)の活用など、あらゆる場面で「曝露(薬剤投与や介入)がアウトカム(治療効果や副作用)に与える影響」を明らかにする必要があります。
しかし、観察研究では交絡因子の影響を受けやすく、単純な比較では因果効果を正しく推定できません。そこで登場するのが 層別解析(stratified analysis) です。
層別解析は、交絡因子ごとにデータを分けて解析することで、交絡の影響を制御し、因果効果をより正確に推定する手法です。本記事では、層別解析の基本概念から、製薬業界での応用、また平均因果効果(ATE)を解説します。
層別解析とは何か
層別解析とは、交絡因子を基準にデータを層(stratum)に分け、それぞれの層で曝露とアウトカムの関係を評価する方法です。
例:喫煙と肺がんの関係
- 交絡因子:年齢
- 若年層と高齢層に分け、それぞれで喫煙と肺がんの関係を評価する
- 各層でのオッズ比やリスク比を算出し、全体の因果効果を推定する
このように、層別解析は「交絡因子を固定した条件下での因果効果」を推定するアプローチです。
製薬業界での具体例
例1:新薬の有効性評価
- 曝露:新薬投与
- アウトカム:疾患改善
- 交絡因子:重症度
重症度が高い患者は新薬を投与されやすく、同時に改善しにくい傾向があります。この場合、重症度で層別化して解析することで、交絡の影響を減らし、新薬の効果をより正確に推定できます。
例2:副作用リスク評価
- 曝露:薬剤使用
- アウトカム:副作用発現
- 交絡因子:性別
性別によって副作用の発現率が異なる場合、性別で層別化して解析することで、薬剤の副作用リスクを適切に評価できます。
Mantel-Haenszel法
層別解析の代表的な方法が Mantel-Haenszel法 です。
これは、複数の層で得られたオッズ比を統合し、全体のオッズ比を推定する方法です。
製薬業界では、臨床試験や観察研究で「交絡因子を調整したオッズ比」を報告する際によく用いられます。
平均因果効果の推定
層別解析で得られるのは「各層における因果効果」です。しかし、研究者や規制当局が知りたいのは「全体としての因果効果」です。
そこで用いられるのが 平均因果効果(ATE) です。ATEは、各層で推定した因果効果を、層の大きさ(重み)に応じて平均したものです。
式で表すと:
\[ATE = \sum_{s} P(S=s) \cdot (E[Y|X=1,S=s] – E[Y|X=0,S=s])\]
ここで
- S:交絡因子(例:性別)
- X:曝露(薬剤使用)
- Y:アウトカム(副作用発現)
つまり、層ごとの因果効果を母集団に合わせて重み付け平均することで、全体の因果効果を推定できるのです。
具体例を用いて説明していきます。
- S:交絡因子(例:冠動脈疾患既往)
- X:曝露(アスピリン投与)
- Y:アウトカム(5年間の冠動脈疾患発生)
DAGで表すと下記のようになります。
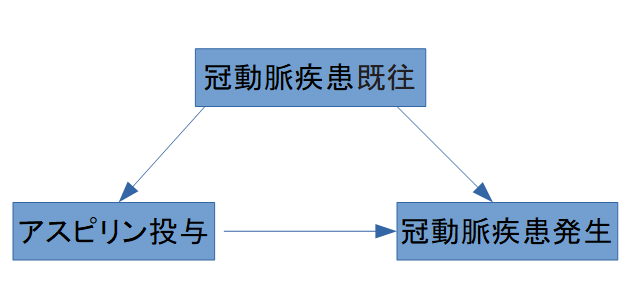
観察された結果が以下とします。
| 全体 | 冠動脈疾患既往あり | 冠動脈疾患既往なし | ||||
| 冠動脈疾患発生 | 合計 | 冠動脈疾患発生 | 合計 | 冠動脈疾患発生 | 合計 | |
| アスピリン投与 | 32 | 500 | 30 | 300 | 2 | 200 |
| アスピリン非投与 | 129 | 2500 | 60 | 200 | 69 | 2300 |
| 合計 | 161 | 3000 | 90 | 500 | 71 | 2500 |
| \[\text{関連RD}=\frac{32}{500}-\frac{129}{2500}\]\[=0.012\] \[\text{関連RR}=\frac{32}{500}\div\frac{129}{2500}\]\[=1.240\] | \[\text{因果関連}RD_{\text{既往あり}}\]\[=\frac{30}{300}-\frac{60}{200}\]\[=-0.2\] \[\text{因果関連}RR_{\text{既往あり}}\]\[=\frac{30}{300}\div\frac{60}{200}\]\[=0.333\] | \[\text{因果関連}RD_{\text{既往なし}}\]\[=\frac{2}{200}-\frac{69}{2300}\]\[=-0.02\] \[\text{関連}RR_{\text{既往なし}}\]\[=\frac{2}{200}\div\frac{69}{2300}\]\[=0.333\] | ||||
アスピリン投与と冠動脈疾患発生リスクとの正の関連が示唆されますが,因果RD や因
果RR とは異なると考えられます。
そこで、冠動脈疾患既往あり群となし群に層別するとアスピリン投与の有無を「仮想的な介入」の有無と見なせるようになり,冠動脈疾患既往ありの層となしの層のそれぞれを標的集団とする因果RD や因果RR を求められます。この層別解析の結果は,アスピリン投与により冠動脈疾患発生リスクが低下したことを示唆しています。
次に平均因果効果を推定していきます。
以下は仮想的に集団全員にアスピリンが投与されたときのデータとなります。こちらは架空のデータとなります。
- 冠動脈疾患既往ありの集団内では交絡がないので,実際にアスピリンを投与された人たちとアスピリンを投与されなかった人たちは、比較可能な集団と考えられ,アスピリンの投与以外の理由で冠動脈疾患発生のリスクは変わらないと考えられます。したがって、アスピリンを投与されなかった200 人が仮想的にアスピリン投与の介入を受けたとしたら冠動脈疾患発生のリスクは10%で、20 人(期待イベント発生数)に冠動脈疾患が発生しただろうと考えられます。
- アスピリン投与を受けなかった2300 人が仮想的にアスピリン投与を受けた場合は,冠動脈疾患発生のリスクは1%(期待イベント発生数=23)と考えられます。
| 冠動脈疾患既往あり | 冠動脈疾患既往なし | |||||
| 事実 | 仮想的介入 | 冠動脈疾患発生 | 合計 | 冠動脈疾患発生 | 合計 | |
| アスピリン投与 | アスピリン投与 (実際と同じ) | 30 | 300 | 2 | 200 | |
| アスピリン非投与 | アスピリン投与 (反事実) | ? [20] | 200 | ? [23] | 2300 | |
| 合計 | 30+[20] | 500 | 2+[23] | 2500 | ||
| 反事実リスク=\(\frac{75}{3000}=0.025\) | ||||||
次に、仮想的に集団全員にアスピリンが投与されなかったときのデータを見ていきます。こちらも架空のデータとなります。
| 冠動脈疾患既往あり | 冠動脈疾患既往なし | |||||
| 事実 | 仮想的介入 | 冠動脈疾患発生 | 合計 | 冠動脈疾患発生 | 合計 | |
| アスピリン投与 | アスピリン非投与 (反事実) | ? [90] | 300 | ? [6] | 200 | |
| アスピリン非投与 | アスピリン投与 (実際と同じ) | 60 | 200 | 69 | 2300 | |
| 合計 | [90]+60 | 500 | [6]+69 | 2500 | ||
| 反事実リスク=\(\frac{225}{3000}=0.075\) | ||||||
以上より、集団全員がアスピリンを投与されたときの反事実リスクは0.025、集団全員
がアスピリンを投与されなかったときの反事実リスクは0.075 と推定されるので,因果RD=-0.050,因果RR=0.333となります。
このように、観察データから反事実的データを考えて穴埋めすることで、反事実リスクを推定できます。これは、曝露群・非曝露群別に実際に観察したデータを交絡因子により層別してリスクを計算し、集団全員に占める各層の人数で重み付けて平均していることに
なります。この方法を,「層別解析に基づく標準化」 と呼びます。
実務での活用ポイント
製薬会社でATEを推定することは、以下の場面で特に重要です。
新薬の有効性評価:患者背景を考慮した上で、全体としての効果を推定
副作用リスク解析:サブグループごとのリスク差を確認しつつ、全体のリスクを評価
規制当局への申請:FDAやEMAに提出する資料では、層別解析とATEの両方を提示することで、解析の透明性と妥当性を高められる
まとめ
今回は層別解析と平均因果効果(ATE)について解説いたしました。層別解析は、交絡因子を基準にデータを分け、それぞれの層ごとに因果効果を推定する手法です。さらに、各層で得られた因果効果を統合することで、平均因果効果(ATE)を推定することができます。ATEは「全体として曝露がアウトカムに与える影響」を示す指標であり、製薬業界における意思決定に直結する重要な役割を果たします。したがって、因果推論を実務に活かすためには、層別解析とATEの両方を正しく理解し、適切に報告することが不可欠となります。