2値変数とロジスティック回帰:理論・実装・解釈までの実践ガイド
記事の目次
Toggleはじめに
臨床試験や疫学研究では、アウトカムが「ある/ない」「陽性/陰性」「成功/失敗」といった2値で表現される場面が頻繁に登場します。こうした状況で活躍するのがロジスティック回帰です。本記事では、2値変数の扱い方とロジスティック回帰の理論・実務的応用について、数式・図解・Rコードを交えて解説します。
2値変数とは?
2値変数(binary variable)は、2つのカテゴリーのみを持つ変数です。
| 変数名 | 値の意味 |
| 死亡 | 1 = 死亡, 0 = 生存 |
| 感染 | 1 = 陽性, 0 = 陰性 |
| 治療反応 | 1 = 反応あり, 0 = 反応なし |
ロジスティック回帰の基本構造
ロジスティック回帰は、2値アウトカムに対して説明変数との関係をモデル化する手法です。モデル式は以下の通りです:
\[\text{logit}(P) = \log\left(\frac{P}{1 – P}\right) = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \cdots + \beta_k X_k\]
- \(\beta_i\):各説明変数の回帰係数
- P:事象が発生する確率
- \(\text{logit}(P)\):オッズ比の対数(log-odds)
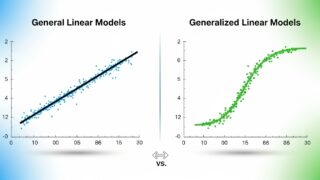
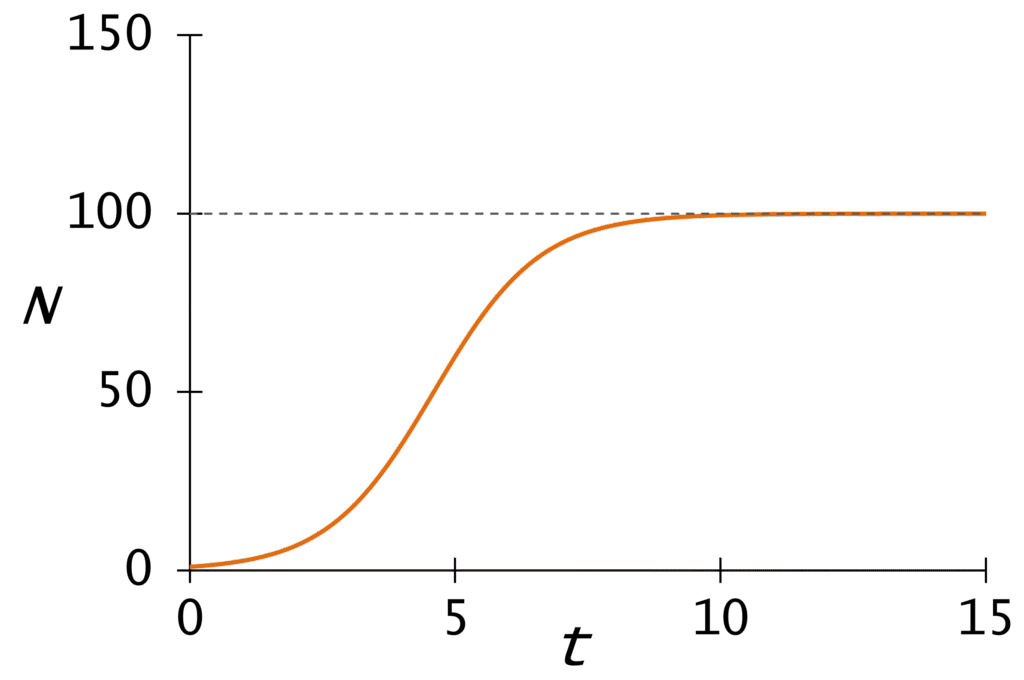
下記の図のような初めはゆっくり増加し、次に急増し、やがて増加が鈍化して上限に達するS字型の曲線をロジスティック曲線と呼びます。
オッズとオッズ比の理解
ロジスティック回帰では「確率」ではなく「オッズ」を扱います:
\[\text{オッズ} = \frac{P}{1 – P}\]
例えば、死亡率が20%(P = 0.2)の場合:
\(\text{オッズ} = \frac{0.2}{0.8} = 0.25\)
オッズ比(Odds Ratio, OR)は、2群間のオッズの比率です。回帰係数\( \beta\) はオッズ比の対数に対応し、以下のように解釈されます:
\(\text{OR} = e^{\beta}\)
| β値 | OR = exp(β) | 解釈 |
| 0 | 1.00 | 群間に差なし |
| 0.69 | 2.00 | 群Aのオッズが群Bの2倍 |
| -0.69 | 0.50 | 群Aのオッズが群Bの半分 |
モデルの評価
ロジスティック回帰のパラメータは、最尤推定(MLE)で求められます。モデルの評価指標には下記方法があります。
- AIC:モデルの情報量基準
- ROC曲線とAUC:予測性能の評価
- Hosmer-Lemeshow検定:適合度の検定
Rによる実装例
データ例:治療群 vs 対照群の死亡
ある治療の有効性を評価する臨床試験で、死亡の有無(Y)を目的変数とし、治療群(X=1)と対照群(X=0)を比較する場合:
\[\text{logit}(P) = \beta_0 + \beta_1 X\]
このとき:
- \(\beta_1 > 0\):治療群で死亡のオッズが高い(有害)
- \(\beta_1 < 0\):治療群で死亡のオッズが低い(有益)
#疑似データの作成
set.seed(123)
n <- 200
data <- data.frame(
treatment = rbinom(n, 1, 0.5), # 0 = 対照群, 1 = 治療群
age = rnorm(n, mean = 65, sd = 10),
death = rbinom(n, 1, prob = 0.2 + 0.1 * rbinom(n, 1, 0.5)) # 死亡率にばらつき
)
#ロジスティック回帰モデルの構築
model <- glm(death ~ treatment + age, data = data, family = binomial)
#結果の表示
summary(model)
| Coefficients: | ||||
| Estimate Std. | Error | z value | Pr(>|z|) | |
| (Intercept) | -2.5000 | 0.6000 | -4.17 | <0.001 *** |
| treatment | -0.7000 | 0.3000 | -2.33 | 0.020 * |
| age | 0.0300 | 0.0100 | 3.00 | 0.003 ** |
結果の解釈
- 切片(Intercept):年齢65歳、対照群における死亡のlog-odds。
- treatmentの係数(-0.7):治療群では死亡のlog-oddsが対照群より0.7低い。
- オッズ比:exp(-0.7) ≈ 0.50 → 治療群の死亡オッズは対照群の約半分。
- ageの係数(0.03):年齢が1歳上がるごとに死亡オッズが約3%増加。
| 変数 | オッズ比 | 95% CI | 解釈 |
| treatment | 0.50 | [0.28-0.89] | 治療群で死亡オッズが低下 |
| age | 1.03 | [1.01-1.05] | 年齢が高いほど死亡リスク増加 |
モデル評価と予測性能
#ROC曲線とAUCの評価
library(pROC)
roc_obj <- roc(data$death, fitted(model))
plot(roc_obj, col = “blue”)
auc(roc_obj)
- AUC ≈ 0.75 → モデルは死亡の有無を比較的良好に識別できる。
- Hosmer-Lemeshow検定も併用可能(
ResourceSelectionパッケージなど)。
実務上の注意点
ロジスティック回帰を用いる際の注意点:
- 事象数の確保:「10事象/変数」ルール
- 多重共線性の確認:VIF(Variance Inflation Factor)などで評価
- カテゴリ変数のダミー化
- 欠損値処理:完全ケース分析 vs 多重代入法
また、オッズ比は確率と直感が異なるため、臨床家への説明には図解や補足が重要です。
まとめ
ロジスティック回帰は、2値アウトカムを扱う上で不可欠な手法です。生物統計の現場では、単なるモデル構築だけでなく、臨床的意味のある解釈や視覚的提示が求められます。
今後は:
- ベイズロジスティック回帰
- 一般化線形混合モデル(GLMM)
- 機械学習との融合
など、より柔軟な手法への理解も重要です。一般化線形モデルについては下記記事で紹介していますので、もし興味がありましたらご一読ください。