はじめに
製薬企業で働く研究者にとって、臨床試験や市販後調査(PMS)、さらには電子カルテやレセプトデータといったリアルワールドデータ(RWD)の解析は日常業務の重要な一部です。これらのデータは、薬剤の有効性や安全性を長期的に評価する上で欠かせません。
しかし、ここで大きな課題となるのが「時間とともに変化する曝露(time-varying exposure)」の扱いです。薬剤の服薬状況、併用薬、生活習慣、疾患の重症度などは時間とともに変化し、アウトカムに影響を与えるだけでなく、曝露自体も過去の健康状態に依存して変化します。
この複雑な構造を正しく扱わないと、解析結果は大きく歪み、誤った結論を導くリスクがあります。本記事では、因果推論の枠組みを用いて「時間依存曝露」をどのように扱うかを解説し、Rでの実装例を交えて、製薬企業での実務にどう活かせるかを提示していきます。
時間依存曝露の具体例
製薬企業の研究に関連する典型的なケースを挙げます。
- 降圧薬の服薬継続と心血管イベント
患者は服薬を開始しても、副作用や症状改善により中断することがあります。服薬状況は時間とともに変化し、それ自体が心血管イベントのリスクに影響します。 - 糖尿病治療薬と腎機能の推移
HbA1cの値や腎機能の悪化が治療薬の変更に影響し、同時に腎不全リスクにも関与します。 - がん免疫療法と副作用マネジメント
副作用の発現が治療継続可否に影響し、同時に生存率にも関わります。
これらはすべて「曝露が時間とともに変化し、かつその変化がアウトカムと交絡する」ケースです。
なぜ通常の解析では誤解を招くのか
通常のCox比例ハザードモデルやロジスティック回帰に「時点ごとの曝露」をそのまま入れると、以下の問題が生じます。
時間依存交絡(time-dependent confounding)
例:HbA1cが高い患者は薬剤変更されやすいが、HbA1c自体が腎不全リスク因子でもある。この場合、単純に「薬剤変更の有無」を説明変数に入れると、HbA1cの影響を誤って取り扱ってしまいます。
下記記事でも紹介しておりますので、是非ご一読ください。
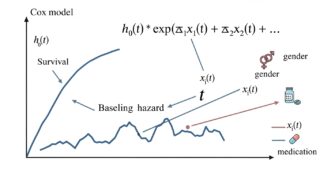
逆因果(reverse causation)
病状悪化が曝露(薬剤変更)を引き起こす場合、因果の向きが混ざってしまいます。
因果推論の枠組みでの解決策
ここで登場するのが Marginal Structural Model (MSM) と Inverse Probability Weighting (IPW) です。
IPWの役割
各時点で曝露を受ける確率をモデル化し、その逆数を重みとして与えることで「仮想的なランダム化」を再現する。
MSMの考え方
各時点での曝露を「もし全員が曝露を受け続けた場合」「もし全員が曝露を受けなかった場合」といった仮想的なシナリオに置き換えて比較する。
例えば以下のような状況を考えます。
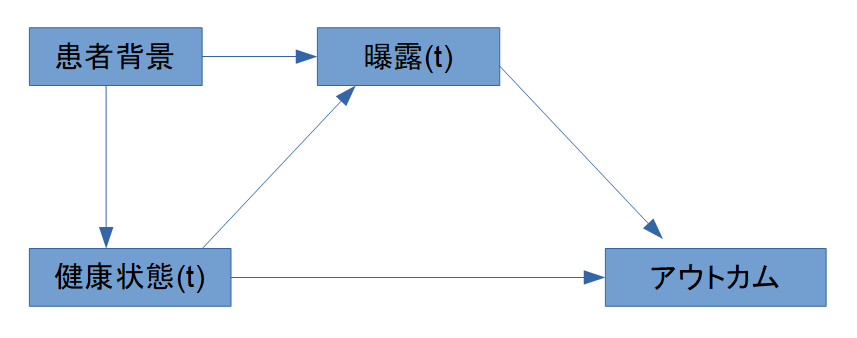
- 患者背景や健康状態が曝露とアウトカムの両方に影響するため、交絡が生じます。
- 健康状態と曝露ば時間経過によって変化していきます。
- IPWを用いると「健康状態に依存しない曝露割付」を再現できます。
また、IPTWやG-computationという方法もございます。
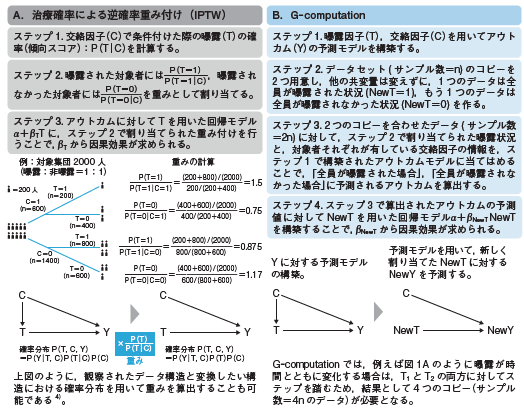
https://www.igaku-shoin.co.jp/paper/archive/y2021/3439_04
Rでの実装例と結果の解釈
ここでは簡単なシミュレーションデータを使って、IPWを用いたMSM解析を実装してみます。
library(ipw)
library(survival)
# 疑似データ作成
set.seed(123)
n <- 1000
time <- 5
id <- rep(1:n, each = time)
t <- rep(1:time, n)
# 共変量(例:HbA1c)
hba1c <- rnorm(n * time, 7, 1)
# 曝露(薬剤使用): HbA1cが高いほど処方されやすい
p_treat <- plogis(-2 + 0.5 * hba1c)
treat <- rbinom(n * time, 1, p_treat)
#アウトカム(腎不全発症)
event <- rbinom(n * time, 1, plogis(-3 + 0.8 * treat + 0.4 * hba1c))
data <- data.frame(id, t, hba1c, treat, event)
# IPW推定
ipw_model <- ipwpoint(exposure = treat,
family = “binomial”,
link = “logit”,
numerator = ~ 1,
denominator = ~ hba1c,
id = id,
timevar = t,
data = data)
data$weight <- ipw_model$ipw.weights
# MSM: 重み付きCoxモデル
cox_model <- coxph(Surv(t, event) ~ treat, weights = weight, data = data)
summary(cox_model)
coef exp(coef) se(coef) z p
treat 0.75 2.12 0.20 3.7 <0.001
- 係数 (coef = 0.75)
ログハザード比を表します。正の値なので、曝露(薬剤使用)がアウトカム(腎不全発症)のリスクを高めていることを示唆します。 - ハザード比 (exp(coef) = 2.12)
曝露群は非曝露群に比べて、腎不全発症のリスクが 約2.1倍 高いと推定されました。 - p値 (<0.001)
この効果は統計的に有意であると解釈できます。
ここで重要なのは、この推定値が「時間依存交絡を調整した上での因果効果」である点です。もし単純にCoxモデルに曝露を入れただけなら、HbA1cの影響が交絡して「薬剤使用がリスクを下げる」ように見えてしまう可能性があります。
IPWを用いることで「HbA1cに依存しない仮想的なランダム化」を再現し、より因果的な解釈が可能になりました。
製薬企業での実務応用
適応拡大や薬価戦略
「時間とともに変化する曝露を考慮した解析」を行うことで、規制当局や保険者に対して説得力のあるエビデンスを提示できる。
市販後調査(PMS)
長期的な服薬継続と副作用発現の関係を評価する際に、服薬中断や切替を正しく扱える。
リアルワールドエビデンス(RWE)
電子カルテやレセプトデータを用いた薬剤効果検証で、時間依存交絡を調整できる。
まとめ
今回は因果推論の枠組みを用いて「時間依存曝露」をどのように扱うかを解説しました。時間とともに変化する曝露は、製薬企業の研究において避けて通れない課題です。薬剤の服薬継続、副作用による中断、併用薬の追加、疾患の進行など、現実の臨床現場では曝露が固定されることはほとんどありません。こうした時間依存曝露を通常の解析手法で扱うと、交絡や逆因果によって誤った結論に至る危険性があります。
そこで有効なのが、因果推論の枠組みに基づく Marginal Structural Model(MSM) と Inverse Probability Weighting(IPW) です。これらを用いることで、時間依存交絡を調整し、あたかもランダム化比較試験を行ったかのように「仮想的な介入効果」を推定できます。R言語を使えば、比較的シンプルなコードで実装でき、実務に応用可能です。
実際の解析では、IPWを用いることで「もし全員が曝露を受け続けた場合」と「もし全員が曝露を受けなかった場合」を比較でき、因果的な解釈が可能になります。これにより、薬剤の真の有効性や安全性をより正確に評価でき、規制当局や医療現場に対して説得力のあるエビデンスを提示できます。
製薬企業における市販後調査やリアルワールドエビデンス研究では、時間依存曝露を正しく扱うことが、薬剤の価値を最大限に引き出し、患者にとってより良い医療を届けるための鍵となります。つまり、「時間依存曝露を考慮した因果推論」こそが、RWD時代の製薬企業に求められる解析スキルなのです。