はじめに
統計学には大きく二つの流派があります。頻度論とベイズ統計です。両者は「確率」をどう解釈するかで立場が異なります。頻度論は「長期的な頻度」として確率を捉え、ベイズ統計は「信念の度合い」として確率を扱います。
製薬業界でも医薬品の効果を評価したり、限られたデータから意思決定を迫られる場面に立ったとしたら、ベイズ統計は強力な武器になります。
従来の頻度論では「データだけ」に基づいて結論を出しますが、ベイズ統計では「これまでの知識や経験」も組み込んで推論できます。特に臨床試験や規制科学の現場では、患者数が限られる希少疾患や早期開発段階での意思決定において、ベイズ的アプローチが注目されています。本稿ではベイズ統計入門として、頻度論との違いやR言語での実装例を紹介していきます。
頻度論の考え方
頻度論では、パラメータは固定された未知の定数とみなし、データは確率的に変動するものと考えます。
例えば「コインの表が出る確率 p」は実際に存在する固定値であり、我々はその値を直接知ることはできません。観測データ(コイン投げの結果)を繰り返し集めることで、推定や検定を行います。
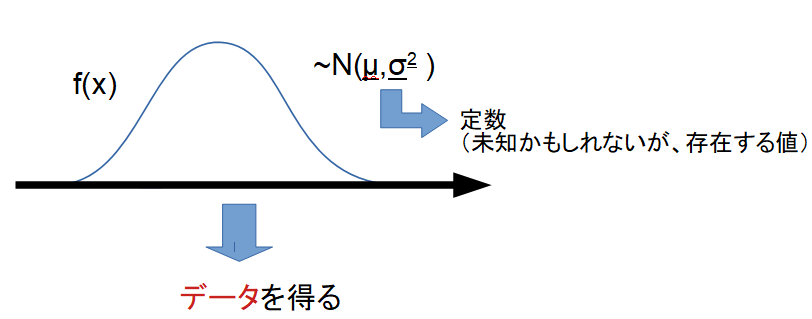
頻度論の統計学では、母数を定数として扱います。つまり。その「定数」で定められた確率分布に従って、データが生起したと考え、データの生起確率の妥当性を検討していきます。
正規分布の場合は以下のようなイメージです。
- 仮説検定:帰無仮説を立て、観測データがその仮説の下でどの程度稀かを評価する(p値)。
- 信頼区間:母集団パラメータが含まれる範囲を、長期的な頻度の観点から保証する。
頻度論の強みは、長い歴史と理論的基盤、そして多くの標準的手法が確立されている点です。一方で「事前の知識を反映できない」「結果の解釈が直感的でない」などの課題もあります。
ベイズ統計の考え方
ベイズ統計では、パラメータを確率変数とみなし、データは固定された観測結果と考えます。
つまり「コインの表が出る確率 p」そのものに確率分布を与え、我々の不確実性を表現します。
このとき重要なのがベイズの定理です。
\[P(\theta |D)=\frac{P(D|\theta )\cdot P(\theta )}{P(D)}\]
- \(\theta\) :未知のパラメータ
- D:観測データ
- \(P(\theta )\):事前分布(prior)
- \(P(D|\theta )\):尤度(likelihood)
- \(P(\theta |D)\):事後分布(posterior)
事前分布に自分の信念や過去の知識を反映し、観測データ(尤度)を通じて更新することで、事後分布として新しい知識を得るのがベイズ統計の特徴です。
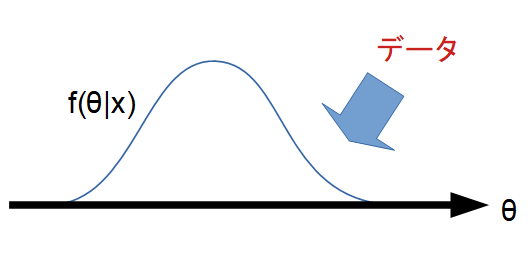
図で表現すると、ベイズ統計学は母数のどの値がどれくらいの確率でその生起に関与したかを考えていきます。
生起のしやすさが、母数の値ごとに異なるので、母数\(\theta\)が変数となります。
頻度論とベイズ論の違いの整理
| 観点 | 頻度論 | ベイズ統計 |
| 確率の解釈 | 長期的な頻度 | 信念の度合い |
| パラメータ | 固定された未知の定数 | 確率変数 |
| データ | 確率的に変動 | 固定された観測値 |
| 推論の結果 | 点推定・信頼区間 | 事後分布 |
| 事前知識 | 反映できない | 反映可能 |
臨床試験データを模したRコード例
ここでは「新薬とプラセボを比較する小規模試験」を想定します。
例:新薬群20例中12例が改善、プラセボ群20例中6例が改善。
# データ
drug_success <- 12
drug_total <- 20
placebo_success <- 6
placebo_total <- 20
#事前分布(非情報的:Beta(1,1))
alpha_prior <- 1
beta_prior <- 1
# 事後分布のパラメータ
alpha_drug <- alpha_prior + drug_success
beta_drug <- beta_prior + (drug_total – drug_success)
alpha_placebo <- alpha_prior + placebo_success
beta_placebo <- beta_prior + (placebo_total – placebo_success)
# サンプリングによる差の分布
set.seed(123)
n_sim <- 10000
p_drug <- rbeta(n_sim, alpha_drug, beta_drug)
p_placebo <- rbeta(n_sim, alpha_placebo, beta_placebo)
diff <- p_drug – p_placebo
# 結果の要約
mean(diff > 0) # 新薬が有効である確率
quantile(diff, c(0.025, 0.5, 0.975)) # 95%信用区間
解釈

mean(diff > 0)が 0.9以上なら「新薬がプラセボより有効である確率が90%以上」と解釈できます。
今回の事例では、新薬がプラセボより有効である確率が90%以上と解釈できます。- 信用区間(credible interval)は「パラメータがその範囲に含まれる確率」を直接表すため、頻度論の信頼区間より直感的に解釈することが可能です。
医薬品開発でのケーススタディと規制当局の視点
規制科学での位置づけ:FDAやPMDAは、医療機器や希少疾患領域でのベイズ的手法の活用をガイダンスで認めています。
課題:患者数が少なく、従来の試験や頻度論では検出力不足となります。
ベイズ的解決策:過去の試験や類似薬剤のデータを事前分布として組み込み、少数例でも有効性を評価可能となる事例がございます。
FDAのガイダンス
米国FDAは2006年に「Guidance for the Use of Bayesian Statistics in Medical Device Clinical Trials」を発表し、医療機器の臨床試験におけるベイズ統計の活用を公式に認めています。この中でFDAは次のように述べています:
“Bayesian methods can be particularly useful in the design and analysis of medical device clinical trials, especially when prior information is available and can be incorporated into the analysis.”
(訳:ベイズ法は、特に事前情報を利用できる場合、医療機器の臨床試験の設計や解析において有用である。)
PMDA(日本医薬品医療機器総合機構)の見解
PMDAもベイズ統計の活用に関心を示しており、「第4回DSRT ベイズ統計学の医薬品の臨床開発での活用について」の資料では、FDAガイダンスを参照しつつ次のように整理しています:
「ベイズ統計学は、既存データを有効に活用できる点で有用であるが、事前分布の設定や透明性の確保が重要である」
また、日本製薬工業協会の研究班による「希少疾患領域の臨床試験におけるベイズ流アプローチの適用に関する基本指針」(2021年)でも、以下のように明記されています:
「ベイズ流アプローチは、希少疾患領域における小規模臨床試験の効率化に資するものであり、事前情報の適切な活用が求められる」
まとめ
今回は頻度論とベイズ統計についての違いを中心に解説いたしました。ベイズ統計は、これまでの知識や経験を新しいデータによって更新していく仕組みであり、医薬品開発や規制科学の分野で実用的に活用されています。記事内で紹介したRコード例を通じて、事前分布から観測データを経て事後分布へと知識が更新されていく流れを実際に体験することができます。特に希少疾患や小規模試験のようにデータが限られる状況では、ベイズ的アプローチが意思決定を支える重要な方法論として大きな役割を果たしています。