生存時間解析の導入と基礎概念〜生存時間とハザード関数を中心に〜

記事の目次

はじめに

生存時間解析（Survival Analysis）は、ある事象が発生するまでの時間を解析する統計手法です。
ここでいう「事象」は、必ずしも「死亡」に限らず、再発、機器の故障、離職、契約終了など、時間経過とともに発生するイベント全般を指します。
臨床試験や疫学研究では、患者が治療開始から死亡または再発するまでの期間を評価することが多く、生存時間解析は医療統計の中核的手法となっています。そこで今回は生存時間解析に関する基礎的な概念を中心に紹介していこうと思います。

生存時間データの特徴

生存時間解析が通常の回帰分析や平均比較と異なるのは、打ち切り（Censoring）と非正規分布の存在です。

打ち切り（Censoring）
研究終了時点でイベントが発生していない場合や、途中で追跡不能になった場合、その時点までの情報しか得られません。
例：試験終了時にまだ生存している患者 → 「右打ち切り（Right-censoring）」

非負かつ右に裾の長い分布
生存時間は0未満にならず、分布は右に長く伸びることが多い。

生存時間の定義と生存関数

生存時間 T は、イベント発生までの時間を表す確率変数です。
生存関数 S(t) は、時刻 t までにイベントが発生しない確率を表します。

\[S(t) = P(T > t)\]

生存関数S(t)の特徴

S(0) = 1（開始時点では全員生存）
S(t) は単調非増加
\(\lim_{t \to \infty} S(t) = 0\)（十分長い時間が経てば全員イベント発生）

ここで確率変数Tを生存時間、f(t)をその確率密度関数とする。このとき、ある時間tまでに死亡する確率は、以下のような累積確率分布関数で表現できる。

\[F(t) = Pr(T < t) = \int_{0}^{t}f(t)dt\]

また、生存関数S(t)を累積確率分布関数で表すと下記のようになります。

\[S(t) = Pr(T \geq t) = 1 – F(t)\]

ハザード関数の定義と直感

ハザード関数（Hazard Function）は、時刻 t において、まだイベントが発生していない対象が、その瞬間にイベントを起こす「瞬間的なリスク率」を表します。

定義式：

\[h(t) = \lim_{\Delta t \to 0} \frac{P(t \leq T < t + \Delta t \mid T \geq t)}{\Delta t}\]

直感的には「死亡率」とは異なり、累積ではなく瞬間的な発生率であり、生存している集団の中で、その瞬間にイベントが起こる割合

生存関数とハザード関数の関係

生存関数 S(t) とハザード関数 h(t) は密接に関連しています。
\[h(t) = \lim_{\Delta t \to 0} \frac{P(t \leq T < t + \Delta t \mid T \geq t)}{\Delta t}\]
\[ = \lim_{\Delta t \to 0} \frac{P(t \leq T < t + \Delta t)}{\Delta t} \times \frac{1}{Pr(T>t)}\]
\[ = \lim_{\Delta t \to 0} \frac{F(t + \Delta t) – F(t)}{\Delta t} \times \frac{1}{S(t)}\]

ここで微分することで下記のようになります。
\[\lim_{\Delta t \to 0} \frac{F(t + \Delta t) – F(t)}{\Delta t} = F'(t) = f(t)\]

そのため、以下が成立します。

\[h(t) = \frac{f(t)}{S(t)}\]

さらに、下記のように表すこともできます。
\[f(t) = -\frac{dS(t)}{d(t)}\]
\[h(t) = \frac{d}{dt}[log(S(t))]\]

ここで\(H(t) = \int_{0}^{t}h(t)dt\)とすると、下記のように表すことができる。

\(S(t)=exp[-H(t)]\)
\(H(t)=-log(S(t))\)

H(t)は累積ハザード関数（Cumulative Hazard Function）と呼ばれています。

これらから、ハザード関数が分かれば生存関数が求まり、その逆も可能です。

具体例：指数分布モデル

最も単純なモデルは、ハザードが一定の指数分布（Exponential Distribution）です。

指数分布について

確率密度関数：\(f(t;\theta)=\theta exp[-\theta t]\)

期待値：\(E(T) = \frac{1}{\theta}\)

分散：\(Var(T) = \frac{1}{\theta^{2}}\)

累積分布関数：\(F(t;\theta)=\int^{t}_{0}\theta exp[-\theta t]dt=1-exp[-\theta t]\)

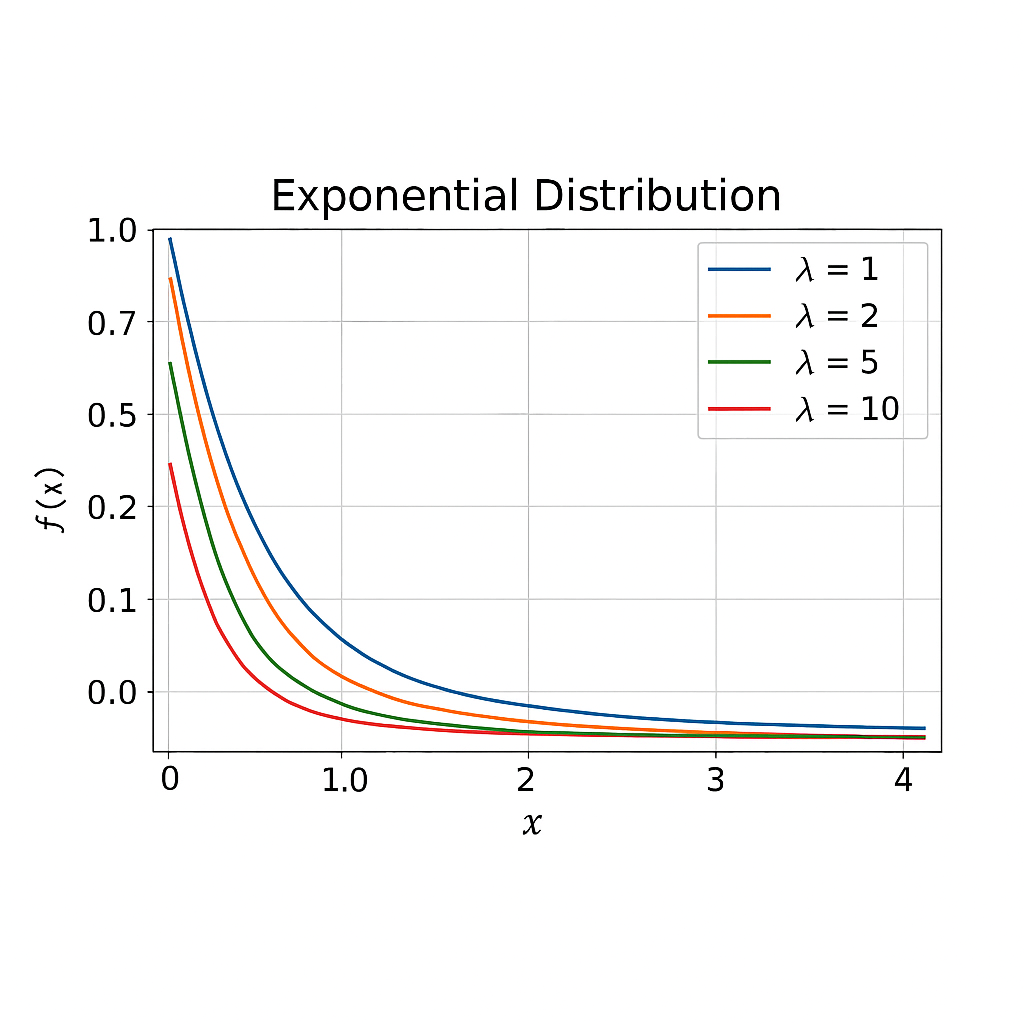
指数分布のハザード関数、生存関数、累積ハザード関数は以下のようになります。

ハザード関数：

\[h(t) = \theta \quad (\theta > 0)\]

生存関数：

\[S(t) = e^{-\theta t}\]

累積ハザード関数：

\[H(t;\theta)=\theta t\]

ハザード関数の形と意味

ハザード関数の形状は、イベント発生のパターンを示します。

ハザード関数の形状

山型（バスタブ曲線）：初期故障期 → 安定期 → 摩耗期（工学分野で多い）
単調減少型：初期リスクが高く、時間とともに低下（例：手術後の合併症）
単調増加型：時間とともにリスク上昇（例：加齢による疾患）

実務での利用例

生存時間解析は様々な分野で解析が行われております。

臨床試験：治療群と対照群の生存曲線比較（Kaplan–Meier法、Log-rank検定）

社会科学：離職までの期間分析

製造業：製品寿命の評価、保証期間設定

まとめ

今回は生存時間解析の導入と基礎概念について解説いたしました。生存時間解析は「イベントまでの時間」を扱う統計手法です。他の解析と異なる点は打ち切りという概念と右に裾が長くなることです。生存関数 S(t) は「生き残る確率」、ハザード関数 h(t) は「瞬間的なリスク率」を表しており、両者は累積ハザード関数を介して密接に関連しております。ハザードの形状は現象のメカニズムを示唆しております。今後は生存時間解析の代表的な解析（Kaplan–Meierやログランク検定、Cox比例ハザードモデル解析等）を紹介していこうと思います。
また、生存時間解析についておすすめの書籍も紹介いたしますので、興味がある方はご参考ください。