はじめに
統計的仮説検定において「p値」は、研究者や規制当局が結果を解釈する際の最も基本的な指標の一つです。臨床試験や薬剤評価の現場では、p値が有意水準(通常は5%)を下回るか否かが、治療効果の有無を判断する重要な基準となります。しかし、p値の定義や性質は、検定統計量が連続分布に従う場合と離散分布に従う場合とで大きく異なってきます。特に離散分布に基づく検定では、p値が「保守的」になりやすく、検出力の低下を招くことが知られています。この問題を緩和する方法の一つとして提案されてきたのがmid-p値です。
本稿では、まず連続分布と離散分布におけるp値の違いを整理し、次にmid-p値の定義と特性を解説していきます。さらに、製薬業界におけるmid-p値の利用シーンを具体的に紹介し、実務的な意義を考察していこうと思います。
連続分布におけるp値
連続分布に基づく検定(例:t検定、F検定、正規分布に基づくZ検定など)では、検定統計量が連続的に変化するため、p値は帰無仮説の下で「観測された統計量以上に極端な値が得られる確率」として自然に定義される。
この場合、p値は一様分布性を持ち、帰無仮説が真であるときにp値が0から1の間で一様に分布することが保証される。したがって、有意水準\(\alpha\)で検定を行えば、第一種過誤率はちょうど\(\alpha\)に一致する。そのため、p値の期待値は0.5となります。
これから、連続分布に基づく検討統計量のp値が一様分布に従うことを一様分布となることを数理的に証明していきたいと思います。この導出は統計検定1級でも出題されますので、一度確認しておくことは重要かと思います。
[証明]
\(\mu_{t}\)を観測値の帰無仮説の確率密度関数、\(F(t)\)を\(\mu_{t}\)の累積分布関数、\(\mu_{p}\)をp値の確率密度関数、\(F(p)\)を\(\mu_{p}\)の累積分布関数とします。目標は観測値が帰無仮説に従うとき、\(\mu_{p}\)が[0,1]上の一様分布であることを示していくことです。
p値は[0,1]上の値しかとらないため、
$$
\begin{eqnarray}
\mu_p=
\begin{cases}
1&(0 \leq p \leq 1)\\
0&(else)
\end{cases}
\end{eqnarray}
$$
\(\mu_{p}\)の累積分布関数\(F_p(x)\)は下記のようなります。
\begin{eqnarray}
F_p(x)=
\begin{cases}
\int_{-\infty}^{x} 0 dx = 0 &(x < 0)\\
\int_{-\infty}^{0} 0 dx + \int_{0}^{x} 1 dx = x&(0 \leq x \leq 1)\\
\int_{-\infty}^{0} 0 dx + \int_{0}^{x} 1 dx + \int_{1}^{\infty} 0 dx= 1&(x \ge 1)
\end{cases}
\end{eqnarray}
これより、\(F_{p} = p\)であることを示せれば、\(\mu_p\)が[0,1]上の一様分布に従うことがわかります。
観測値がtの時のp値をyとすると、p値の定義より、
$$
\begin{eqnarray}
y &=& \mu_t ({x|x \ge t})\\
&=& 1 – \mu_t ({x|x \le t})\\
&=& 1 – F_t(t)
\end{eqnarray}
$$
例えば、yは以下のような赤斜線部分のp値を示します。
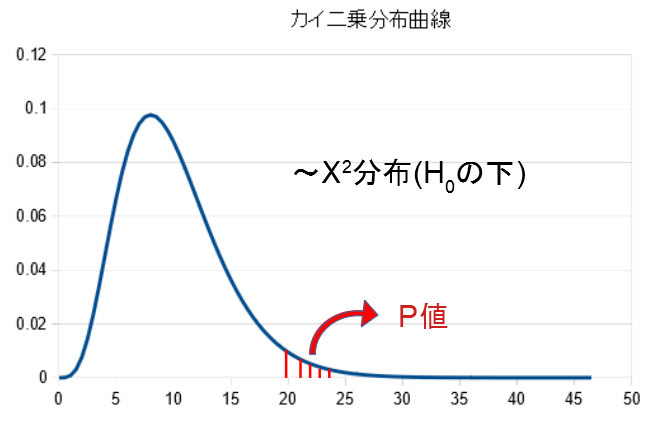
また\(F_t(t)\)は分布関数の条件から、\(F_t\)は単調増加することから、
$$
\begin{eqnarray}
y \le p & \leftrightarrow & 1 – y \ge 1 – p\\
& \leftrightarrow & F^{-1}_{t}(1 – y) \ge F^{-1}_{t}(1 – p)\\
\end{eqnarray}
$$
以上より、
$$
\begin{eqnarray}
F_{p}(p) &=& \mu_p ({y|y \le p})\\
&=& \mu_{t}({F_{t}^{-1}(1-y)|F^{-1}_{t}(1 – y) \ge F^{-1}_{t}(1 – p)})\\
&=& 1 – \mu_{t}({x | x < F_{t}^{-1}(1-p)})\\
&=& 1 – F_{t}(F_{t}^{-1}(1-p))\\
&=& 1 – (1-p)\\
&=& p
\end{eqnarray}
$$
よって、\(F_p(p) = p\)より、p値が[0,1]上の一様分布であることが示されて、下記となる。
$$
\begin{eqnarray}
\mu_p(p)=
\begin{cases}
p&(0 \leq p \leq 1)\\
0&(else)
\end{cases}
\end{eqnarray}
$$
P値が\(\alpha\)以下となる確率は
$$
\begin{eqnarray}
\mu_{p}(p \le \alpha) &=& F_{p}(\alpha)\\
&=& \alpha (0 \le \alpha \le 1)\\
\end{eqnarray}
$$
pの期待値は、下記のようになる。
$$
\begin{eqnarray}
E[p] &=& \int p \cdot \mu_{p}(p) dp\\
&=& \int_{- \infty}^{0} p \cdot 0 dp + \int_{0}^{1} p dp + \infty_{1}^{\infty} p \cdot 0 dp\\
&=& 1/2 =0.5
\end{eqnarray}
$$
離散分布におけるp値の問題
一方、二項分布や超幾何分布、ポアソン分布など離散分布に基づく検定では事情が異なります。検定統計量が取り得る値は飛び飛びであり、p値も「飛び飛びの値」となります。
[具体例]
例:二項分布の二側正確検定(n=2, p=0.5)
設定:
\[X \sim \mathrm{Bin}(n=2,\;p=0.5),\quad H_0: p=0.5\]
帰無仮説の下での確率は\(P(X=0)=0.25,\quad P(X=1)=0.5,\quad P(X=2)=0.25.\)
二側正確p値の定義(“確率が観測値以下の事象の総和”):
観測値 x に対して、その確率 P(X=x) 以下の確率を持つ点の確率総和を二側p値とする。
各観測値のp値:
観測値 \(x=0:P(X=0)=0.25 \Rightarrow P(X=0)\le 0.25 \text{ の点は } k=0,2.\)
よって、\(p(0)=P(X=0)+P(X=2)=0.25+0.25=0.5\)
観測値 x=2: 同様に\(p(2)=0.5\)
観測値 x=1:\(P(X=1)=0.5 \Rightarrow P(X=k)\le 0.5 \text{ の点は } k=0,1,2 \text{(全点)}\)
よって、\(p(1)=P(X=0)+P(X=1)+P(X=2)=1.0\)
p値の分布:
$$
\begin{eqnarray}
p(X)=
\begin{cases}
0.5 & \text{with prob } 0.25 \text{(}X=0\text{)},\\
1.0 & \text{with prob } 0.5 \text{(}X=1\text{)},\\
0.5 & \text{with prob } 0.25 \text{(}X=2\text{)}.
\end{cases}
\end{eqnarray}
$$
p値の期待値
\[\mathbb{E}[p(X)]=0.25\cdot 0.5 + 0.5\cdot 1.0 + 0.25\cdot 0.5= 0.125 + 0.5 + 0.125 = 1.0\]
- この具体例では、帰無仮説の下で \(\mathbb{E}[p(X)] = 1.0\) と明確に 0.5 を上回る。
- 直観的には、離散分布では「中心の質量」が大きく、二側の正確p値が観測値の確率質量を含めて“まとめて”足し込むため、p値が大きくなりやすい。結果として、p値は一様分布よりも右に歪み、期待値が 0.5 を超える(保守的)傾向が生じる。
- これが、離散検定で有意水準を下回りにくく検出力が落ちる理由であり、mid-p値が提案されてきた背景である。
その結果、以下のような問題が生じる。
- 保守性(conservativeness)
有意水準\(\alpha\)を設定しても、実際の第一種過誤率は\(\alpha\)を下回ることが多い。つまり「有意」と判定されにくくなる。
例:二項検定でnが小さい場合、p値は0.05より小さくならないケースが多い。 - 検出力の低下
保守的であるがゆえに、真に効果が存在しても有意と判定できないリスクが高まる。
この問題は、特に小標本サイズの臨床試験や希少疾患領域で顕著である。製薬業界では、症例数が限られる試験設計が少なくないため、離散分布に基づく検定の保守性は実務上の大きな課題となる。
mid-p値の定義と考え方
mid-p値は、この保守性を緩和するために提案された修正p値である。定義は次の通りである。
- 通常のp値(exact p値)は、観測された統計量以上に「極端」な結果が得られる確率の総和である。
- mid-p値は、観測された統計量そのものの確率の「半分」を加えることで定義される。
数式で表すと、
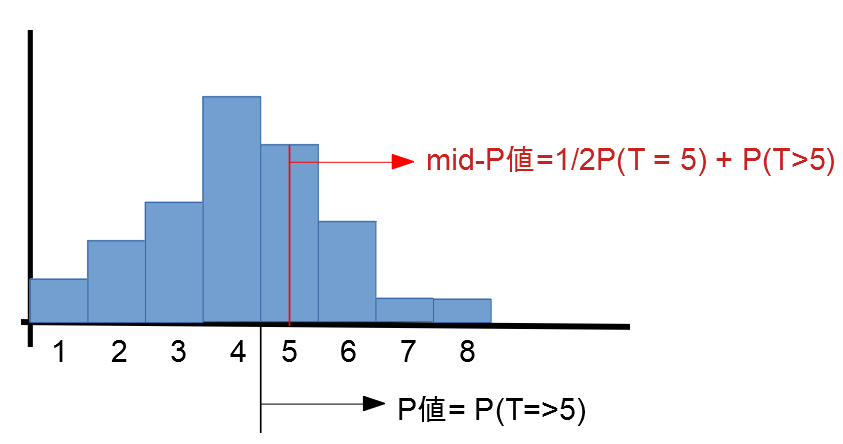
\[p_{\text{mid}} = P(T > t_{\text{obs}}) + \tfrac{1}{2} P(T = t_{\text{obs}})\]
ここで、\(T\)は検定統計量、\(t_{\text{obs}}\)は観測値である。
図で表すと以下のようになる。
- mid-p値はexact p値よりも小さくなる傾向がある。
- 保守性を緩和し、検出力を改善する。
- 一方で、第一種過誤率が名目水準をわずかに上回る可能性があるため、厳密な「サイズ保証」は失われる。
このため、mid-p値は「exact p値と漸近的p値の中間的な妥協案」と位置づけられる。
mid-p値の利用シーン(製薬業界)
製薬業界では、規制当局への申請や臨床試験の解析において、統計的検定の選択は極めて重要である。mid-p値は以下のような場面で活用が検討されている。
小規模臨床試験
希少疾患や初期探索的試験では、症例数が限られるため二項検定やFisherの正確確率検定が用いられることが多い。
- exact p値は保守的すぎて有意差を検出できない場合がある。
- mid-p値を用いることで、効果を見逃すリスクを低減できる。
マクネマー検定(対応のある二値データ)
治療前後の改善有無を比較するマクネマー検定では、mid-p値が推奨されるケースが多い。
- exact検定は保守的で検出力が低い。
- mid-p値は第一種過誤率と検出力のバランスが良い。
安全性シグナルの検出
副作用の発現率を比較する際、症例数が小さいとexact検定が使われる。mid-p値を用いることで、過度に保守的な判定を避け、潜在的な安全性シグナルを見逃さないようにできる。
規制当局との議論
ICHガイドラインやPMDA/EMA/FDAの統計的原則では、基本的にはexact検定や漸近的検定が標準である。しかし、探索的解析や補助的解析においてmid-p値を提示することは、結果の解釈を補強する材料となり得る。特に希少疾患領域では、mid-p値の利用が実務的に容認されるケースもある。
実例:二項検定における比較
例えば、ある新薬の奏効率を評価する小規模試験を考える。
- n = 10例、うち8例が奏効。
- 帰無仮説:奏効率 = 0.3
このとき、
- exact p値 ≈ 0.054
- mid-p値 ≈ 0.027
となる。exact p値では有意水準5%をわずかに超えるため「有意差なし」と判定されるが、mid-p値では「有意差あり」と解釈できる。この差は、臨床的意思決定に直結する可能性がある。
批判と限界
- 厳密な第一種過誤率の制御が保証されない。
- 規制当局の正式な承認解析においては、標準的な方法としては認められていない。
- 解釈に注意が必要であり、補助的な指標として位置づけるのが妥当。
まとめ
連続分布と離散分布におけるp値の違いを整理し、次にmid-p値の定義と特性を解説していきました。連続分布に基づく検定ではp値は一様分布性を持ち、第一種過誤率を正確に制御できます。一方、離散分布に基づく検定ではp値が飛び飛びとなり、保守的に偏るため期待値が0.5を超え、検出力が低下します。この問題を緩和する方法としてmid-p値が提案され、観測値の確率を半分だけ加えることで過度な保守性を和らげることができます。製薬業界では小規模試験や希少疾患領域、安全性シグナル検出などで有用性が高く、規制当局との議論においても補助的指標として活用されます。mid-p値は厳密なサイズ保証を欠くが、実務的にはexact p値と漸近的p値の中間的な役割を果たし、臨床試験の意思決定を支える重要な選択肢となりえます。