はじめに
臨床試験では、複数の仮説を同時に検証する場面が少なくありません。主要評価項目が複数ある場合や、主要評価項目と主要副次評価項目の両方で有意性を示したい場合、または異なる患者集団や用量群を検証する場合などです。このような状況では、多重性による第一種過誤率（Family-Wise Error Rate: FWER）の増加を制御する必要があります。
Gatekeeping法は、このFWERを強い意味で（strong control）制御しつつ、事前に定めた優先順位に従って仮説を検証する多重性調整手法です。
基本的な考え方
Gatekeeping法では、複数の仮説を仮説族（family）に分け、優先度の高い仮説族を「ゲート」として設定します。先行する仮説族で有意性が確認されない限り、後続の仮説族の検定には進めません。
Gatekeeping法の基本条件は：
\[\text{If } \forall j, \; H_{1j} \text{ is not rejected} \quad \Rightarrow \quad \text{Do not test } F_2, F_3, \dots, F_m\]
FWER制御のため、各仮説族内ではBonferroni法やHolm法などの多重性調整を適用します。
Bonferroni法やHolm法については下記の記事で紹介しておりますので、興味ありましたら一読ください。
主なタイプ
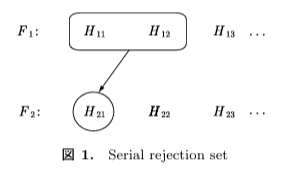
Serial Gatekeeping（直列型）
特徴：厳格な順序制御。前段階で失敗すると後続は検定できない。
構造：仮説族を固定順序で並べ、前の族が全て有意であれば次に進む。
例：主要評価項目（F1）→主要副次評価項目（F2）
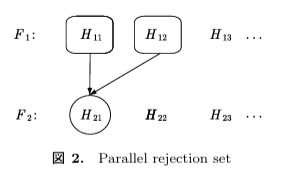
Parallel Gatekeeping（並列型）
特徴：柔軟性が高く、臨床的に重要な複数の主要評価項目を扱いやすい。
構造：前の仮説族のうち少なくとも1つが有意であれば次に進む。
例：複数の主要評価項目のうち1つでも有意なら副次評価項目へ。
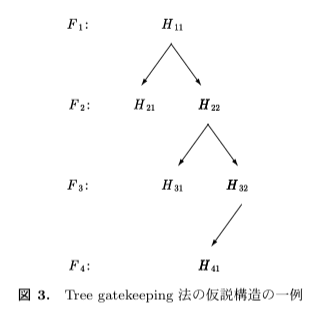
Tree Gatekeeping（樹形型）
特徴：複雑な試験デザインや複数のサブグループ解析に対応可能。
構造：仮説間の関係をツリー構造で表現し、分岐ごとに進行条件を設定。
例：主要評価項目Aが有意なら副次評価項目A1へ、Bが有意ならB1へ。
自分の経験では主要評価項目が有意だった場合服地評価項目の仮説検定を行うSerial Gatekeeping法を適用する事例を多く見てきました。
実務での適用例
複数用量群試験：高用量群で有意性を確認後、中用量群の有効性を検証する場合。
承認申請試験：主要評価項目で有意性を示した後、副次評価項目の有効性を主張する場合。
国際共同試験：主要評価項目の有意性を全体集団で確認後、特定の地域集団（例：日本人集団）での有意性を検証する場合。
メリットと注意点
- FWERを強い意味で制御可能。
- 仮説の優先順位を明確化できる。
- 規制当局（FDA, EMA, PMDA）での受容性が高い。
- 前段階で失敗すると後続の検定ができないため、試験全体の戦略に影響。
- 事前に仮説構造と進行条件を明確に定義する必要がある。
- 柔軟性と厳格性のバランスを設計段階で検討する必要がある。
注意点でもありますが、仮説構造やどのような手法を明確に定義・検討する必要があります。そのため、臨床試験を開始する前に規制当局に相談し、検討しておくことが重要かと思います。
まとめ
Gatekeeping法は、複数の仮説を持つ臨床試験において、第一種過誤率を制御しつつ効率的に検証を進めるための強力な手法です。直列型・並列型・樹形型といったバリエーションを理解し、試験目的や評価項目の重要度に応じて適切に選択することが重要です。
参考
https://onlinelibrary.wiley.com/doi/abs/10.1002/pst.291
