「回帰分析って何をしているの?」線を引くだけで理解する入門
記事の目次
Toggleはじめに
統計学を学び始めた人が必ず出てくるのが 回帰分析です。
「式が難しそう」「係数の意味がよく分からない」と感じる人も多いですが、実は本質はとてもシンプルです。
回帰分析とは、データに最もしっくりくる“線”を引くことです。
この記事では、そのような回帰分析を学習したい人に向けて図解を用いてわかりやすく解説いたします。初学者でもスッと理解できるような構成となっておりますので、是非ご一読ください。
回帰分析とは「データに線を引くこと」
まずは次のような散布図を想像してください。
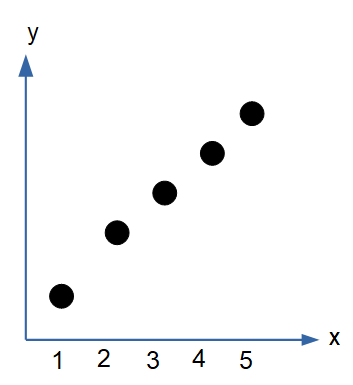
右上がりの関係がありそうですよね。
回帰分析は、この点の集まりに対して 最もよく説明する線(回帰直線) を引く作業です。
たとえばこんな線です。
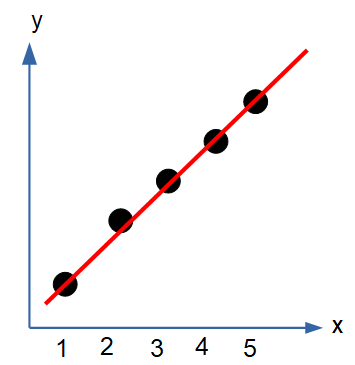
この線が「回帰直線」です。
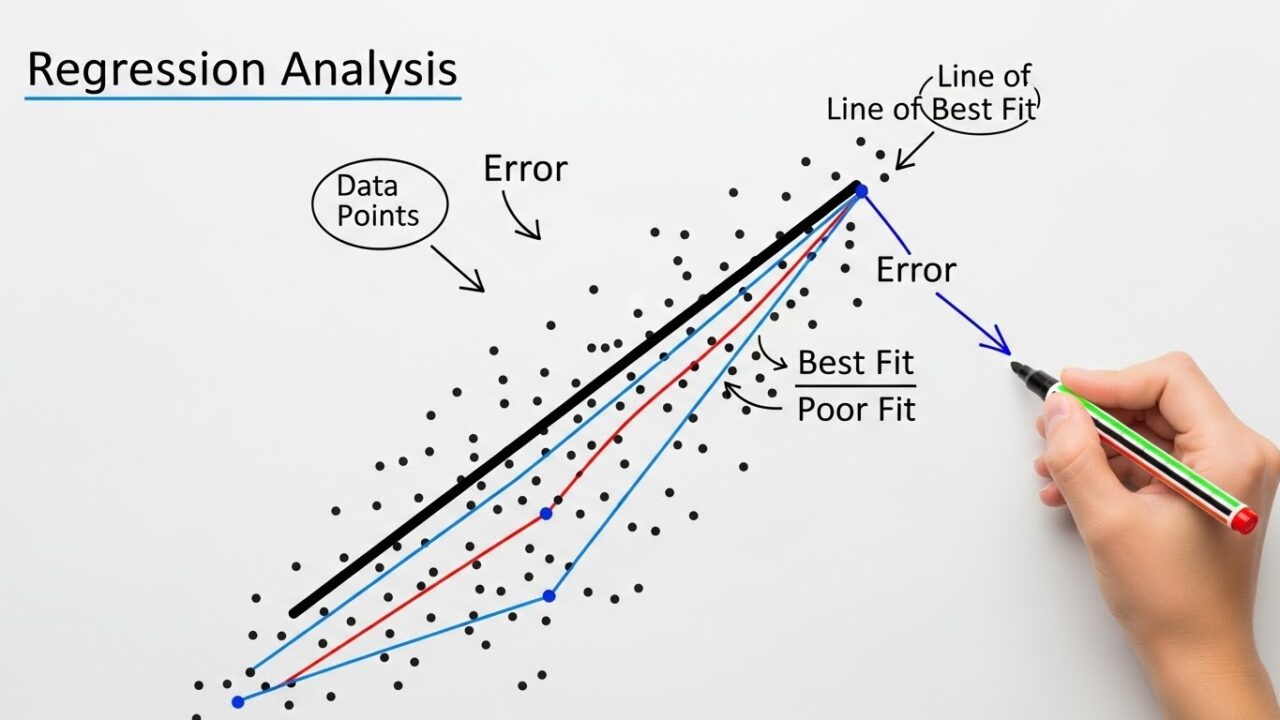
最小二乗法を“線を動かすアニメ”で理解する
では、どうやって「最もよく説明する線」を決めるのでしょうか?
ここで登場するのが 最小二乗法(Least Squares) です。
点と線の“縦の距離”を 残差(residual) と呼びます。
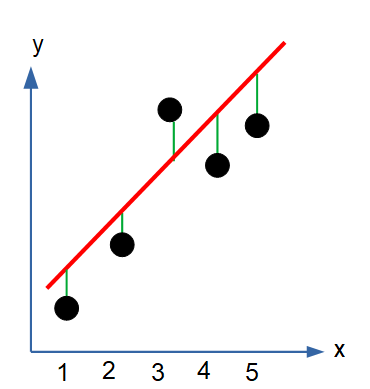
縦の緑の棒が残差です。
最小二乗法は、残差の「二乗」を全部足した値が最も小さくなるように線を調整するという方法です。
なぜ二乗するのか?
- プラスとマイナスを打ち消さないため
- 大きなズレをより強くペナルティにするため
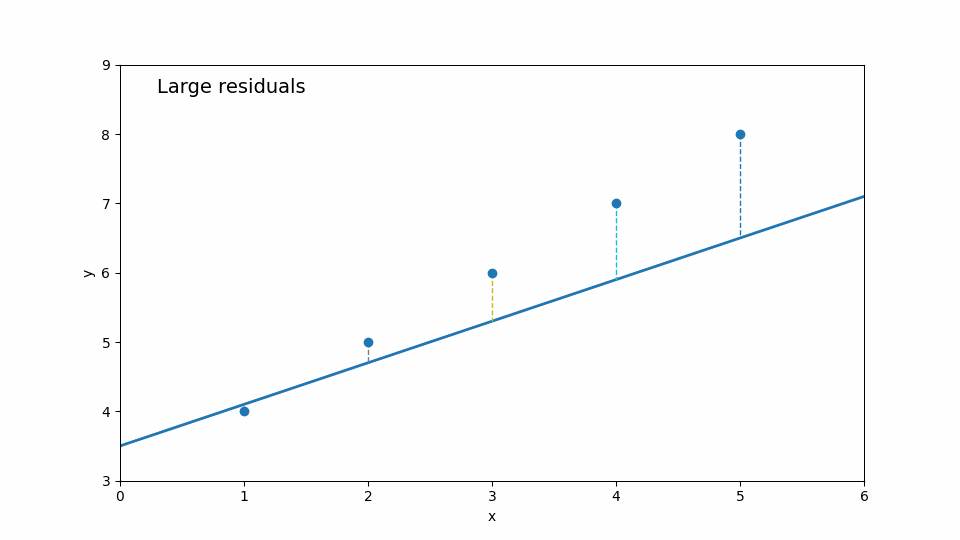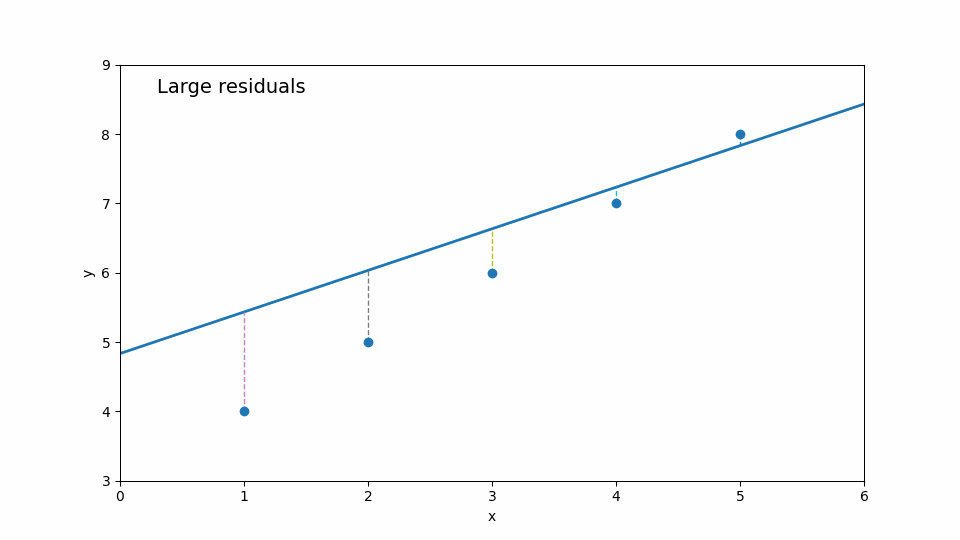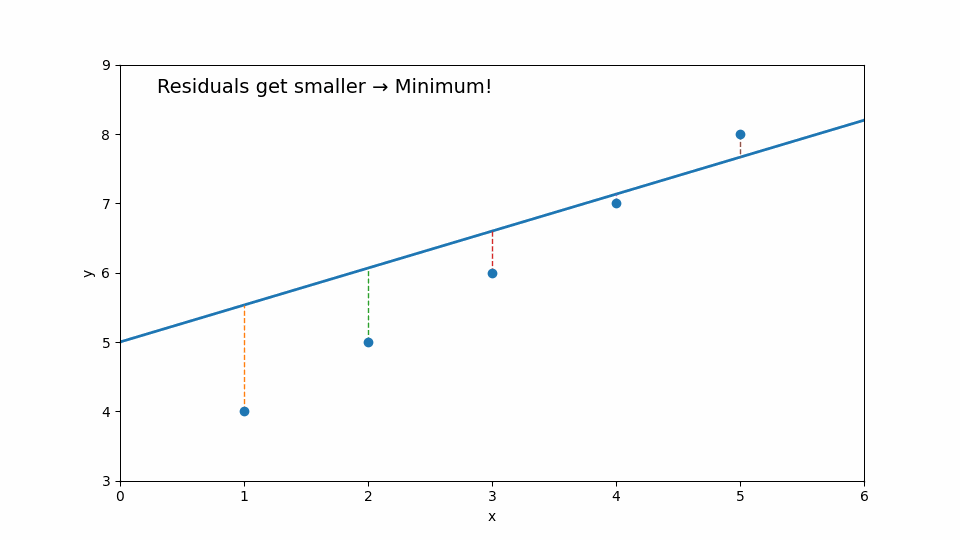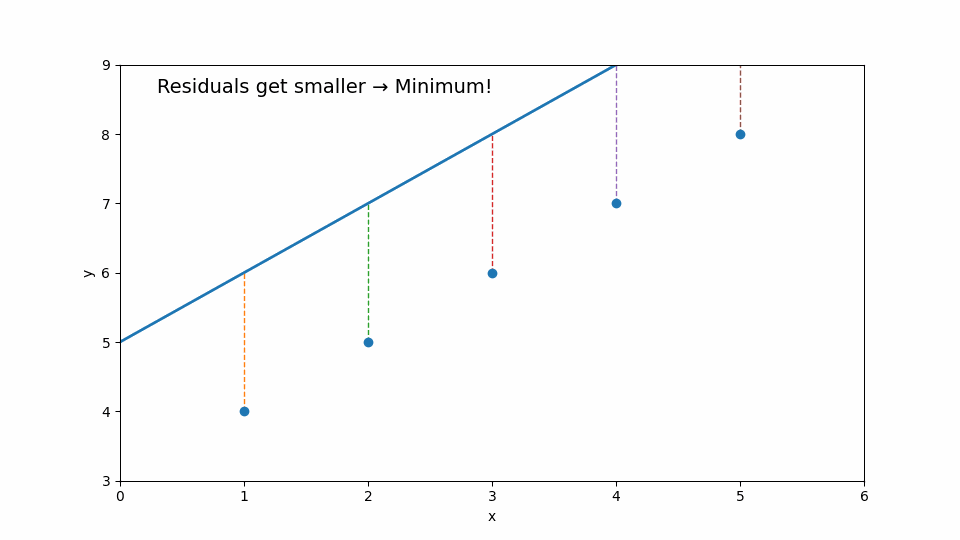
線を上下に動かす、傾きを変える…
そのたびに「点から線までのズレ(残差)」が変わります。
最終的に 残差の合計が最小になる位置 に落ち着く場所を探していきます。
これを最小二乗法といいます。
回帰係数は「1単位変わるとどれだけ動くか」
回帰直線は次の式で表されます。
\[y=a+bx\]
- a:切片(x=0 のときの y)
- b:回帰係数(傾き)
このうち、初心者がつまずきやすいのが 回帰係数 b の意味 です。
b=xが1増えたときに、yがどれだけ増えるか
たとえば、
\[y=2+3x\]
なら、
- x が 1 増えると、y は 3 増える
- x が 2 増えると、y は 6 増える
という意味です。
残差と「モデルの良さ」をどう見るか
回帰分析では、線を引いた後に「どれくらい上手く説明できているか」を評価します。
その代表が 決定係数(R²) です。
- R² = 1 に近い → よく説明できている
- R² = 0 に近い → 説明できていない
ただし、R² が高いからといって「因果関係がある」とは限りません。
ここは初心者が誤解しやすいポイントです。
中級者の壁「多重共線性」を理解する
回帰分析が少しわかってくると、次にぶつかるのが 多重共線性(multicollinearity) です。
これは、説明変数同士が強く相関していると、回帰係数が不安定になるという現象です。
- 回帰係数の標準誤差が大きくなる
- p 値が不安定になる
- モデルの解釈が難しくなる
つまり、「線は引けるけど、意味のある線ではなくなる」 ということです。
多重共線性の直感的な例
たとえば、
- 身長(cm)
- 足の長さ(cm)
を同時に説明変数に入れると、ほぼ同じ情報を二重に入れていることになります。
一方、医薬品開発の解析で実際に起きやすい例です。
- 年齢(連続値)
- 年齢カテゴリ(例:若年・中年・高齢)
これらは当然ながら ほぼ完全に相関しています。
この場合、
- 年齢と年齢カテゴリは同じ情報を二重に入れている
- モデルが「どちらを使うべきか」判断できず混乱する
- 回帰係数が極端な値になったり、符号が逆転したりする
という問題が起きます。
医薬統計では、共変量調整モデル(ANCOVA や Cox 回帰)でよく見落とされるポイントです。
まとめ
回帰分析は、一見すると数式が並ぶ難しい手法に見えますが、その本質はとてもシンプルです。
「データに最もしっくりくる線を引き、その線の傾きから関係性を読み取る」
これが回帰分析のすべてです。
最小二乗法は、線を上下や左右に“動かしながら”残差が最も小さくなる位置を探す仕組みであり、まるでアニメーションのように線が最適な場所へ吸い寄せられていきます。
回帰係数は「x が 1 増えると y がどれだけ変わるか」を示す直感的な量で、データの関係性を読み解くうえで欠かせません。
一方で、説明変数同士が強く相関していると起きる 多重共線性 は、回帰係数を不安定にし、モデルの解釈を難しくする中級者の壁です。
身長と足の長さ、広告費と SNS 広告費、年齢と年齢カテゴリなど、実務でも頻繁に起きる問題であり、適切な対処が求められます。
回帰分析は、データ分析の基礎でありながら、実務でも強力な武器になります。
今回紹介した「最小二乗法のイメージ」「回帰係数の直感」「多重共線性の注意点」を押さえることで、回帰分析の理解は大きく前進します。
ここから先は、残差分析やロジスティック回帰、モデル選択など、さらに深い世界が広がっています。
ぜひ次のステップにも挑戦してみてください。


![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/4aa03195.892069bb.4aa03196.39df6be9/?me_id=1213310&item_id=10335792&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F0655%2F9784130420655.jpg%3F_ex%3D300x300&s=300x300&t=picttext)