【徹底解説】多重代入法(Multiple Imputation)とは?
記事の目次
Toggleはじめに
欠測データは、疫学研究や臨床研究、社会科学データ分析など、あらゆる分野で避けて通れない問題です。
「欠測があるから解析できない…」
「完全症例解析(CC)でいいのでは?」
といった声はよく聞きますが、欠測を安易に無視すると深刻なバイアスが生じることがあります。
そこで登場するのが 多重代入法(Multiple Imputation; MI) です。
本記事では、MI の理論背景から実装のポイント、注意点までを体系的に解説します。
基礎的な多重代入法については以下の記事で紹介しておりますので、是非ご一読ください。

多重代入法とは何か?
多重代入法(MI)は、欠測値を1つの値で埋めるのではなく、複数の plausible(もっともらしい)値で埋めることで、
欠測に伴う不確実性を統計的に正しく反映する方法です。
MI は次の3ステップで構成されます。
■ ステップ1:欠測値を複数回「予測」する(Imputation)
欠測値 \(X_{\mathrm{mis}}\) を、観測データ \((Y,X_{\mathrm{obs}})\) から推定した代入モデルに基づいて予測します。
代入モデルの例:
\[f(X_{\mathrm{mis}}\mid Y,X_{\mathrm{obs}})\]
この予測を K 回(例:20回) 繰り返し、K 個の「見かけ上完全なデータセット」を作成します。
■ ステップ2:各データセットを通常の方法で解析する(Analysis)
K 個のデータセットそれぞれに対して、回帰分析などの通常の統計解析を行います。
すると、K 個の推定値:
\[\hat {\theta }^{(1)},\hat {\theta }^{(2)},\ldots ,\hat {\theta }^{(K)}\]
と、それぞれの分散推定値:
\[\hat {U}^{(1)},\hat {U}^{(2)},\ldots ,\hat {U}^{(K)}\]
が得られます。
■ ステップ3:Rubin のルールで結果を統合する(Pooling)
Rubin(2004)が示した「Rubin のルール」により、K 個の推定結果を統合します。
● 推定値の平均
\[\bar {\theta }=\frac{1}{K}\sum _{k=1}^K\hat {\theta }^{(k)}\]
● 分散の分解
分散は「データ内の不確実性」と「代入間の不確実性」に分けられます。
- 代入内分散(within-imputation variance)
\[\bar {U}=\frac{1}{K}\sum _{k=1}^K\hat {U}^{(k)}\]
- 代入間分散(between-imputation variance)
\[B=\frac{1}{K-1}\sum _{k=1}^K(\hat {\theta }^{(k)}-\bar {\theta })^2\]
- 総分散(total variance)
\[T=\bar {U}+\left( 1+\frac{1}{K}\right) B\]
● 信頼区間
\[\bar {\theta }\pm t_{\nu }\sqrt{T}\]
自由度 \(\nu\) は Rubin の式で計算されます。
【ステップ1:代入モデルの推定】
欠測変数 X1, X2 に対して
X1 ~ Y + X2
X2 ~ Y + X1
のようなモデルを推定
【ステップ2:多重代入(K回)】
1回目:欠測値を予測 → 完全データ1
2回目:欠測値を予測 → 完全データ2
…
K回目:欠測値を予測 → 完全データK
【ステップ3:各データを解析】
完全データ1 → 回帰分析 → θ(1)
完全データ2 → 回帰分析 → θ(2)
…
完全データK → 回帰分析 → θ(K)
【ステップ4:Rubin のルールで統合】
θ = 平均
分散 = within + between
→ 信頼区間を計算
MI が優れている理由
- 欠測の不確実性を正しく反映できる
単一代入(平均値代入・回帰代入)は不確実性を過小評価し、標準誤差が小さくなりすぎる(=過剰な自信) という問題があります。
MI は代入間分散 B を加えることで、この問題を解決します。 - MAR(Missing At Random)を前提に理論的に正当化される
MAR とは:
\[P(R=1\mid X_{\mathrm{mis}},X_{\mathrm{obs}})=P(R=1\mid X_{\mathrm{obs}})\]
欠測が観測データに依存していればよい、という条件です。
MI は MAR の下でバイアスなく推定できる ことが理論的に保証されています。 - 完全症例解析(CC)より効率的
CC は欠測を含む行をすべて捨てるため、サンプルサイズが減り、推定精度が低下します。
MI は観測データを最大限活用するため、標準誤差が小さくなる(=効率が高い) 傾向があります。
MI の実装方法:FCS(MICE)と Joint Modeling
MI の実装として以下の2つが紹介します。
■ Joint Modeling(多変量正規分布など)
欠測変数を含むすべての変数の同時分布を仮定する方法。
例:多変量正規分布
\[(X_1,X_2,\ldots ,X_p)\sim N_p(\mu ,\Sigma )\]
- 利点:理論的に美しい
- 欠点:非正規データや混合データでは扱いにくい
■ FCS(Fully Conditional Specification)= MICE
変数ごとに条件付きモデルを指定し、
連鎖的に代入を行う方法。
例:
- X_1 の欠測 → 回帰モデル \(X_1\sim Y+X_2\)
- X_2 の欠測 → ロジスティック回帰 \(X_2\sim Y+X_1\)
この手法は MICE(Multivariate Imputation by Chained Equations) として広く使われています。
- 利点:柔軟で実装しやすい
- 欠点:収束性の理論保証が難しい場合がある
MI の注意点:正しい代入モデルが必須
MIを実装する際の重要ポイントは次の通りです。
1. 解析モデルと整合した代入モデルを作ること
解析モデルに含める変数は、
代入モデルにも必ず含める必要があります。
例:解析モデルに交互作用 \(X_1\times X_2\) を含めるなら代入モデルにも同じ交互作用を含める。
含めないと、効果が過小評価される ことが知られています。
2. アウトカムを代入モデルに含めること
共変量欠測の場合、アウトカム Y を代入モデルに含めないとバイアスが生じる(Moons et al., 2006)。
3. 代入回数 K は十分大きく
Rubin は「5回で十分」と述べましたが、近年の研究では 20〜100回 が推奨されています。
理由:代入間分散 B の推定精度を高めるため。
MI の限界:MNAR には対応できない
MI は MAR を前提 としています。
欠測が未観測の値に依存する MNAR の場合:
\[P(R=1\mid X_{\mathrm{mis}},X_{\mathrm{obs}})\neq P(R=1\mid X_{\mathrm{obs}})\]
MI はバイアスを生じます。
そのため、MNAR が疑われる場合は:
- パターン混合モデル
- 選択モデル
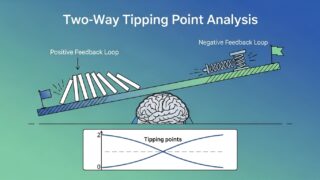
- tipping-point 解析
などの 感度分析 が必須です。
まとめ
多重代入法(MI)は、欠測データ解析における最も信頼性の高いアプローチの一つです。その強みは、欠測値を単に埋めるのではなく、欠測に伴う不確実性そのものを統計的に扱う点にあります。単一代入法のように「1つの値で埋めて終わり」ではなく、複数の plausible な値を生成し、それぞれで解析を行い、Rubin のルールで統合することで、欠測による情報の揺らぎを適切に反映できます。
MI が理論的に正当化されるのは MAR(Missing At Random) を前提とするためであり、観測データに基づいて欠測が生じている状況では、バイアスのない推定が可能です。また、完全症例解析(CC)のようにデータを捨てる必要がないため、推定精度(効率)も高くなります。
一方で、MI の性能は 代入モデルの質に大きく依存します。解析モデルと整合した変数を含めること、アウトカムを代入モデルに入れること、交互作用や非線形項を適切に扱うことなど、モデル構築の注意点を守らなければ、MI であってもバイアスが生じます。また、MNAR(Missing Not At Random)の状況では MI だけでは不十分であり、感度分析が不可欠です。
実装面では、Joint Modeling と FCS(MICE)の2つのアプローチがあり、特に MICE は柔軟性が高く、実務で広く使われています。代入回数は近年では 20〜100 回が推奨され、代入間分散の推定精度を高めることが重要です。
総じて、多重代入法は「欠測があるから仕方ない」と諦めるのではなく、欠測を前提にした科学的に妥当な推定を可能にする方法です。欠測データが避けられないリアルワールドデータ解析において、MI を正しく理解し、適切に実装することは、研究の信頼性を大きく高める鍵となります。