がん臨床試験におけるベイズ流バスケットデザインの理論と実装― 階層ベイズモデル・EXNEXモデル・モデル平均化の応用 ―

記事の目次
Toggleはじめに
近年、分子生物学やゲノミクスの進展により、がん患者は原発巣が同じであっても遺伝子変異やバイオマーカーの違いによって細分化できることが明らかになってきました。これに伴い、特定の分子異常を標的とする治療薬の臨床開発が加速し、従来の「がん種ごとに独立した臨床試験を行う」枠組みでは対応が難しくなっています。
この課題を解決するために考案されたのが バスケット試験です。バスケット試験は、複数のがん種や疾患サブタイプに対して単一の標的治療を評価する試験であり、希少がんや希少フラクションの患者を効率的に登録できる利点があります。しかし、各サブ試験の症例数は少数であるため、統計的推論の精度や部分集団間の関連性評価が大きな課題となります。
本稿では、この課題に対処するための ベイズ流バスケットデザインを解説します。具体的には以下の3つの方法を中心に取り上げます。
- 階層ベイズモデル:部分集団間で情報を借用し、推定精度を高める方法
- EXNEXモデル:交換可能性と非交換可能性を同時に仮定し、柔軟に情報借用を調整する方法
- ベイズ流モデル平均化:部分集団間の均質性をモデル選択の枠組みで評価する方法
さらに、実際のバスケット試験(BRAF-V600試験)のデータを用いたRによる実装例を紹介し、各方法の特徴や有用性を考察します。
本稿では、がん臨床試験におけるベイズ流バスケットデザインの理論的背景と実務的応用を体系的に理解できるようにすることです。数式や図解を交えながら、統計モデルの仕組みと臨床試験デザインへの適用をわかりやすく解説します。
バスケット試験の背景
近年の分子生物学・ゲノミクスの進展により、同じ原発巣を持つがん患者でも遺伝子変異やバイオマーカーの違いによって細分化できることが明らかになりました。次世代シークエンサーの普及により、複数の遺伝子タイプを高速かつ正確に同定できるようになり、プレシジョン・メディシンの臨床開発が加速しています。
従来の第I相~第III相試験をバイオマーカーごとに実施するのは非現実的であるため、複数仮説を効率的に検証する「マスタープロトコル」が考案されました。その中で バスケット試験は「複数のがん種やサブタイプに対して単一の標的治療を評価する」試験であり、希少がんや希少フラクションの患者を効率的に登録できる利点があります。
代表例として以下が挙げられる:
- BRAF-V600試験:BRAF V600変異を有する複数がん種に対するベムラフェニブの有効性を評価
- AcSé試験:ALK, MET, ROS1変異を伴うがん種に対するクリゾチニブの有効性を評価
- NCI-MATCH試験:固形癌・リンパ腫に対し17種以上の標的治療を評価
- TAPUR試験:進行癌に対する複数薬剤の有効性を評価
これらは非盲検・非対照型であり、主要評価項目として奏効率(ORR)が用いられることが多いです。

情報借用の考え方
バスケット試験では各サブ試験の症例数が少なく(20~50例程度)、単独解析では統計的検出力が不足する。そこで、部分集団間の潜在的関連性を考慮し、情報を共有する「情報借用(borrowing information)」の考え方が導入されています。
階層ベイズモデルの基本式
部分集団 j の奏効確率を \(p_j\)、症例数を \(n_j\)、奏効例数を \(r_j\) とすると、以下の二項分布に従います。
\[r_j\sim \mathrm{Binomial}(n_j,p_j)\]
対数オッズを
\[\theta _j=\log \frac{p_j}{1-p_j}\]
と定義し、階層事前分布を
\[\theta _j|\mu ,\tau \sim \mathrm{Normal}(\mu ,\tau ^{-1})\]
さらに、超事前分布として\(\mu\)を正規分布、\(\tau\)がGamma分布を仮定します。
\[\mu \sim \mathrm{Normal}(\mu _0,\sigma ^2),\quad \tau \sim \mathrm{Gamma}(\alpha ,\beta )\]
ここで \(\tau\) の平均値が大きいほど部分集団間の関連性が強く、情報借用の程度が大きくなります。
部分集団\(j\)に対する奏功確率関する尤度関数は、
\[L(\theta_{j}|n_{j},r_{j}) = \binom{n_{j}}{r_{j}}p_{j}^{r_{j}}(1-p_{j})^{n_{j}-r_{j}} = \binom{n_{j}}{r_{j}}\frac{exp(\theta_{j})^{r_{j}}}{\left[1 + exp(\theta_{j}) \right]^{n_{j}}}\]
であるから、階層ベイズモデルの同時事後分布は\(\boldsymbol{\theta}= (\theta_1,\theta_2,…,\theta_J)\), \(\boldsymbol{r}= (r_1,r_2,…,r_J)\), \(\boldsymbol{n}= (n_1,n_2,…,n_J)\)とすると、
\[f(\boldsymbol{\theta},\mu,\tau|\boldsymbol{n},\boldsymbol{r};j=1,…,J)=\left[\prod_{j=1}^{J}L(\theta_j|n_j,r_j)f(\theta_j|\mu,\tau)\right]f(\mu| \tilde{\mu},\tilde{\sigma}^{2})f(\tau|\alpha,\beta)\]
となります。ただし、\(f\)は確率密度関数を表します。
階層ベイズモデルの概念図は下記のようになります。
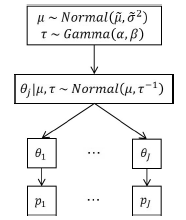
部分集団\(j\)に対する有効性は,事後確率が以下の条件を満たすか否かで判断します。ここで,\(\phi\)は目標奏効確率,qは判断のためのカットオフ値(0~ 1)です。
\[Pr(p_j>\phi|n_j,r_j)>q\]
実際には、試験の中間解析時点で。全部分集団のデータを用いて上記の条件を満たすか否かを確認していきます。このとき、患者登録は早いが奏効率が低い部分集団が存在する可能性を考慮して、中間解析時点までの登録例数に制約を設ける場合もあります。
EXNEXモデル
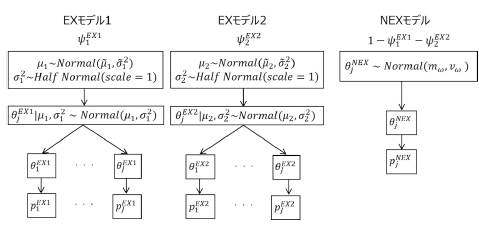
Neuenschwanderら(2016)が提案した EXNEXモデルは、部分集団間に「交換可能(EX)」と「非交換可能(NEX)」が混在する状況を想定します。
- EX(Exchangeable):他の部分集団と情報を共有できる
- NEX(Non-exchangeable):独立に評価すべき部分集団
部分集団 j の奏効確率に対して、確率 \(\pi _j\) でEX分布、確率 \(1-\pi _j\) でNEX分布を仮定します。
\[\theta _j\sim \pi _j\cdot \mathrm{Normal}(\mu ,\sigma ^2)+(1-\pi _j)\cdot \mathrm{Normal}(m_j,v_j)\]
この混合分布をMCMCで推定することで、部分集団ごとに「どの程度情報を借用するか」を柔軟に調整できます。
下記図はEXNEXモデルの概念図となります。
ベイズ流モデル平均化
Simon(2018)は、部分集団別奏効率の均質性を ベイズモデル平均化(Bayesian Model Averaging, BMA)で評価する方法を提案した。
仮説設定
- \(H_0\):全部分集団の奏効確率は等しい
- \(H_1\):各部分集団の奏効確率は独立
各部分集団の奏効確率が「高い\((p_{\mathrm{high}})\)」か「低い\((p_{\mathrm{low}})\)」かを事前確率\( \gamma \)で仮定し、中間解析ごとに事後確率を更新する。
判定基準
部分集団\( j\) の事後確率を \(Pr[p_j=p_{\mathrm{high}}|r,n]\) とすると、
- \(<1-\delta\) :無効と判定し登録中止
- \(1-\delta \leq \cdot \leq \delta\) :登録継続
- \(>\delta\) :有効と判定し登録中止
この枠組みにより、部分集団間の均質性を動的に評価しつつ効率的な試験運営が可能となる。
今後の展望
ベイズ流バスケットデザインは、希少がんや分子サブタイプにおける臨床試験の効率化に大きな可能性を持っています。今後の展望として以下が挙げられます。
- 中間解析の高度化
部分集団間の均質性を逐次評価し、早期に有効性・無効性を判定する仕組みを強化することで、患者負担を軽減しつつ迅速な意思決定が可能となる。 - 感度解析の標準化
EXNEXモデルにおけるチューニングパラメータ(尺度s)の設定は試験結果に影響を与えるため、複数設定を用いた感度解析を標準的に組み込むことが望ましい。 - 規制当局との対話
FDAやPMDAはバスケット試験を探索的POC試験として位置づけているが、承認申請に直結するためには追加検証が必要である。今後は規制当局との協議を通じて、ベイズ流デザインの妥当性や透明性を確保することが重要となる。 - ソフトウェアの普及
Rパッケージ trialr や Stan を用いた実装が整備されつつあり、研究者や製薬企業が容易にベイズ流デザインを試験に組み込める環境が整いつつある。これにより、実務での利用が加速すると期待される。
まとめ
バスケット試験は、分子標的治療の臨床開発において希少がんや多様なサブタイプを効率的に評価するための有力な枠組みである。しかし、各部分集団の症例数が少ないため、統計的推論の精度や部分集団間の関連性評価が課題となります。
本稿では、この課題に対処するためのベイズ流バスケットデザインを紹介しました。階層ベイズモデルは部分集団間で情報を借用し推定精度を高め、EXNEXモデルは交換可能性と非交換可能性を柔軟に扱うことで異質性に対応します。さらに、ベイズ流モデル平均化は部分集団間の均質性をモデル選択の枠組みで評価する方法を提供します。
実際の試験データ(BRAF-V600試験)を用いたRによる実装例からも示されるように、これらの方法は少数例でも安定した推定を可能にし、効率的な試験運営に寄与します。今後は中間解析の高度化、感度解析の標準化、規制当局との対話、ソフトウェアの普及を通じて、ベイズ流バスケットデザインは臨床試験の現場でさらに重要な役割を果たすと期待されます。
参考
がん臨床試験におけるベイズ流バスケットデザインの理論と実装
(2018, 平川) https://cir.nii.ac.jp/crid/1390001288136783616