ベイズ統計と平均リスク・事後リスクの理解
記事の目次
Toggleはじめに
近年、医薬統計や規制科学の分野では、従来の頻度主義的な統計手法に加えて、ベイズ統計の活用が急速に広がっています。特に希少疾患や小規模試験においては、既存の知見を事前分布として取り込み、新たなデータと統合することで、より効率的かつ柔軟な意思決定が可能になります。ベイズ統計の枠組みでは「平均リスク」と「事後リスク」という概念が重要な役割を果たします。平均リスクは事前分布に基づく期待損失を表し、事後リスクは観測データを踏まえた意思決定の最適性を評価します。
本記事では、これらの概念を数式や図を交えて整理し、さらにRコードによる事後分布の可視化やFDA/PMDAにおけるベイズ試験事例を紹介することで、理論と実務の両面から理解を深めていきます。
ベイズ統計の基本枠組み
ベイズ統計は「事前分布」「尤度」「事後分布」の3要素で構成されます。
ベイズの定理は次式で表されます:
\[p(\theta |x)=\frac{p(x|\theta )\pi (\theta )}{\int _{\Theta }p(x|\theta )\pi (\theta )\, d\theta }\]
ここで、\(\pi (\theta )\) は事前分布、\(p(x|\theta )\) は尤度、\(p(\theta |x)\) は事後分布です。
損失関数とリスク
損失関数:推定誤差を定量化する関数。例:二乗誤差損失
\[L(\theta ,t)=(t-\theta )^2\]
リスク関数:損失の期待値
\[R(\theta ,t)=\int (t-\theta )^2f(x|\theta )\, dx\]
リスク関数は統計的決定理論で、予測の良さを評価する指標として用いられます。損失関数を、起こりうる全ての状況について平均化したものです。
平均リスクと事後リスク
平均リスク:事前分布に基づく期待損失
\[r(\pi ,t)=\int R(\theta ,t)\pi (\theta )\, d\theta\]
事後リスク:観測データ後の期待損失
\[r(t|x)=\int L(\theta ,t)p(\theta |x)\, d\theta\]
二乗誤差損失の場合、事後リスクを最小化する推定量は 事後分布の期待値 です。
ここで、以下のように定義します。
平均リスク\(r(\pi ,t)\)を最小にする\(\theta\)の推定量\(T=t(X_{1},…,X_{n})\)があるとき、このTを事前分布\(\pi(\theta)\)に対するベイズ推定量という。
以下でベイズ推定量を導出していきます。
$$
\begin{align}
r(\pi ,t)
&= \int_{\Theta} R(\theta,t)\,\pi(\theta)\, d\theta \\
&= \int_{\Theta} \int_{\mathcal{X}} (t-\theta)^{2} f(x|\theta)\, dx \, \pi(\theta)\, d\theta \\
&= \int_{\mathcal{X}} \underline{\int_{\Theta} (t-\theta)^{2} f(x|\theta)\, \pi(\theta)\, d\theta} \, dx
\end{align}
$$
下線部分を最小にする\(T = t(X_{1},…X_{n})\)を見つけていく。
$$
\begin{align}
\text{下線部分}
&= t^{2}\int_{\Theta} f(x|\theta)\, \pi(\theta)\, d\theta -2t \int_{\Theta}\, \theta\, f(x|\theta)\, \pi(\theta)\, d\theta + \int_{\Theta}\, \theta^{2}\, f(x|\theta)\, dx \, \pi(\theta)\, d\theta \\
&= a(x)t^{2} – 2b(x)t + c(x)\\
&=a(x) \left[t – \frac{b(x)}{a(x)} \right]^{2} – \frac{(b(x))^{2}}{a(x)} + c(x)
\end{align}
$$
よって事前分布\(\pi (\theta) \)に対するベイズ推定量\(T = t(X_{1},…X_{n})\)は、
\[T = \frac{b(x)}{a(x)} = \frac{\int_{\Theta} \theta f(x|\theta)\, \pi(\theta)\, d\theta }{\int_{\Theta} f(x|\theta)\, \pi(\theta)\, d\theta} = \int_{\Theta} \theta \hat{f}(x|\theta)\, d\theta = E[\theta|X = x] \]
これは、事後分布の平均となり、\(\hat{f}(x|\theta)\)を\(X = x\)を与えた時の\(\theta\)の事後分布となります。
具体例(二項分布とベータ分布)
現在、以下のような場合を考えていきます。
- 標本空間:\(\mathcal{X} = [0,1,…,n]\)
- X ~ 二項分布\( \, Bi (n,\theta)\)
- \(f(x|\theta) = \binom{n}{x}\theta^{x}(1-\theta)^{n-x} \, (x=0,1,2,…,n)\)
- \(\theta \in \Theta\) (パラメータ空間) \(\Theta =[0,1]\)
- \(\theta\)の事前分布: ベータ分布 \(Be(a,b)\)
$$
\begin{eqnarray}
\pi(\theta)=
\begin{cases}
\frac{1}{B(a,b)\theta^{a-1}(1-\theta)^{b-1}} & (0 \leq \theta \leq 1)\\
0 & (else)
\end{cases}
\end{eqnarray}
$$
この時、\(\pi(\theta)\)に対する\(\theta\)のベイズ推定量を求めていきます。
ベイズ推定量は上記で求めているので、
$$
\begin{align}
T = E(\theta | X=x) = \int_{\theta}\theta \hat{f}(\theta|x) \, d\theta
&= \int_{\theta}\theta \left( \frac{f(x|\theta)\pi(\theta)}{\int_{\theta}f(x|\theta)\pi(\theta)} \right) \, d \theta\\
&= \frac{\int_{\theta}\theta f(x|\theta)\pi(\theta) \, d \theta}{\int_{\theta} f(x|\theta)\pi(\theta) \, d\theta}\\
&= \frac{\int_{0}^{1}\theta \binom {n}{x} \theta^{x}(1-\theta)^{n-x} \frac{1}{B(a,b)}\theta^{a-1}(1-theta)^{b-1} \, d \theta}{\int_{0}^{1} \binom {n}{x} \theta^{x}(1-\theta)^{n-x} \frac{1}{B(a,b)}\theta^{a-1}(1-theta)^{b-1} \, d \theta}\\
&= \frac{\int_{0}^{1}\theta^{(x+a+1)-1} (1-\theta)^{(n-x+b)-1} \, d \theta}{\int_{0}^{1}\theta^{(x+a)-1} (1-\theta)^{(n-x+b)-1} \, d \theta}\\
&= \frac{B(x+a+1 , n-x+b)}{B(x+a , n-x+b)}
\end{align}
$$
ここで、ベータ関数、ガンマ関数の以下の性質を利用します。
- ベータ関数
\[B(a,b) = \int_{0}^{1}y^{a-1}(1-y)^{b-1} \, dy \]
\[B(a,b) = \frac{\Gamma(a) \Gamma(b)}{\Gamma(a+b)}\] - ガンマ関数
\[\Gamma(a) = \int_{0}^{\infty}x^{a-1}e^{-x} \, dx\]
\[\Gamma(a) = (a-1)\Gamma(a-1)\]
$$
\begin{align}
\text{与式}
&= \frac{\Gamma (x+a+1) \Gamma (n-x+b)}{\Gamma [(x+a+1) + (n-x+b)]} \times \frac{1}{\frac{\Gamma (x+a) \Gamma (n-x+b)}{\Gamma[(x+a)+(n-x+b)]}}\\
&= \frac{\Gamma (x+a+1) \Gamma (n-x+b)}{\Gamma (n+a+b+1)} \times \frac{\Gamma (n+a+b)}{\Gamma (x+a) \Gamma (n-x+b)}\\
&= \frac{(x+a)\Gamma (x+a)}{(n+a+b)\Gamma (n+a+b)} \times \frac{\Gamma (n+a+b)}{\Gamma (x+a)}\\
& = \frac{x+a}{n+a+b}
\end{align}
$$
したがって、\(\pi(\theta)\)に対する\(\theta\)のベイズ推定量は、
\[T = \frac{X+a}{n+a+b}\]
また、リスクについても求めていきます。
$$
\begin{align}
R(\theta , T) = E((T – \theta)^{2})
&= \sum_{x=0}^{n}(T-\theta)^{2} \binom{n}{x} \theta^{x} (1-\theta)^{n-x}\\
&= E(T^{2}) – 2\theta E(T) + \theta^{2}\\
&= V(T) + (E(T))^{2} – 2 \theta E(T) + \theta^{2}
\end{align}
$$
ここで、
\[E(T) = \frac{n \theta +a}{n+a+b}\]
\[V(T) = V\left(\frac{X+a}{n+a+b} \right) = \frac{V(X+a)}{(n+a+b)^{2}} = \frac{V(X)}{(n+a+b)^{2}}= \frac{n\theta(1 – \theta)}{(n+a+b)^{2}}\]
以上より、
\[R(\theta , T) = \frac{n\theta(1-\theta)+(a-(a+b)\theta)^{2}}{(n+a+b)^{2}}\]
Rコードによる事後分布の可視化
以下は、ベータ事前分布と二項尤度から得られる事後分布を可視化する例です。
# パラメータ設定
alpha <- 2; beta <- 2 # 事前分布 Beta(2,2)
n <- 20; x <- 12 # 試行回数と成功数
# 事後分布のパラメータ
alpha_post <- alpha + x
beta_post <- beta + n – x
# 可視化
theta <- seq(0, 1, length=100)
prior <- dbeta(theta, alpha, beta)
posterior <- dbeta(theta, alpha_post, beta_post)
plot(theta, prior, type=”l”, col=”blue”, lwd=2, ylim=c(0, max(posterior)),
ylab=”Density”, xlab=expression(theta))
lines(theta, posterior, col=”red”, lwd=2)
legend(“topright”, legend=c(“Prior”, “Posterior”),
col=c(“blue”,”red”), lwd=2)
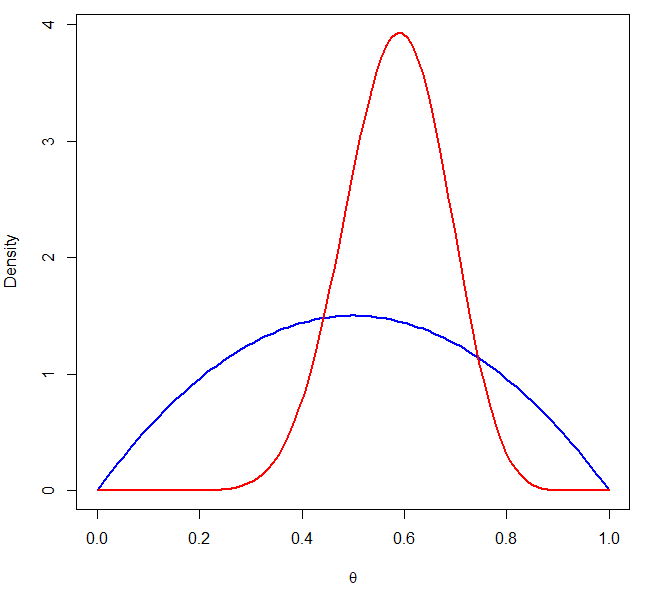
事前分布(青)と事後分布(赤)が重ねて描画され、データによる更新の様子が直感的に理解できます。
FDA/PMDAにおけるベイズ試験事例
- FDA:希少疾患領域や医療機器評価でベイズ的アプローチを採用。既存試験データを事前分布として活用し、小規模試験でも有効性を評価可能。
- PMDA:市販後調査(PMS)やリスク管理計画(RMP)において、ベイズ統計の活用が議論されている。特に希少疾患領域では、事前情報を活用することで効率的な試験設計が可能とされる。
これらの事例は、平均リスクによる事前評価と事後リスクによる観測後意思決定の枠組みが、規制科学に直結していることを示しています。
まとめ
ベイズ統計における平均リスクと事後リスクは、単なる理論的な枠組みにとどまらず、実務的な意思決定に直結する重要な概念です。平均リスクは「事前の性能評価」として、試験設計や戦略立案に活用され、事後リスクは「観測後の最適意思決定」として、得られたデータに基づく推定や判断を支えます。Rコードによる事後分布の可視化は、データ更新の直感的理解を助け、FDAやPMDAの事例はベイズ的アプローチが規制科学においても現実的に受け入れられていることを示しています。今後、希少疾患や個別化医療の領域では、ベイズ統計の応用がさらに広がり、平均リスクと事後リスクの考え方が、より多くの意思決定の基盤となるでしょう。