ベイズ統計における事前分布・事後分布・尤度の関係と共役事前分布
記事の目次
Toggleはじめに
統計学は「不確実性の中で意思決定を行うための学問」と言われます。その中でもベイズ統計は、新しいデータが得られるたびに知識や信念を更新していくという直感的な考え方を数学的に定式化したものです。近年では、医薬品開発や機械学習、マーケティング分析など幅広い分野で活用されており、特に「限られたデータから合理的に結論を導く」場面で強みを発揮します。
ベイズ統計の核となるのは 事前分布・尤度・事後分布 の三者関係です。事前分布は「データを観測する前の信念」、尤度は「観測データがどのパラメータを支持するか」、そして事後分布は「両者を統合した更新後の信念」を表します。さらに、計算を容易にするために導入される 共役事前分布 という概念も重要です。
本記事では、これらの基本的な考え方を数式と図解を交えて解説します。読者が「ベイズ更新」の直感をつかみ、実務や研究に応用できるようになることを目指します。
特に臨床試験や製薬分野では、過去の試験データや専門家の知見を事前分布として組み込み、新しいデータと統合することで、より信頼性の高い意思決定を支援できる点が注目されています。
下記記事ではベイズ統計の導入として紹介しておりますので、ご興味ありましたら是非一読ください。

ベイズ統計の基本的な考え方
ベイズ統計は「信念の更新」を数学的に表現する枠組みです。
頻度論的統計学では「パラメータは固定された未知の真値」とみなしますが、ベイズ統計では「パラメータそのものを確率変数」として扱います。
その中心にあるのが ベイズの定理 です。
\[p(\theta \mid x)=\frac{p(x\mid \theta )\, p(\theta )}{p(x)}\]
- \(p(x)\):周辺尤度(正規化定数)
- \(\theta\) :未知パラメータ
- \(x\):観測データ
- \(p(\theta )\):事前分布(データ観測前の信念)
- \(p(x\mid \theta )\):尤度(データが得られる確率)
- \(p(\theta \mid x)\):事後分布(データ観測後の信念)
ここで\(p(x)\):周辺尤度(正規化定数)は、定数のため、上記式は以下のように表現することもできます。
\[p(\theta \mid x) \propto p(x\mid \theta )\, p(\theta )\]
つまり、事後分布は「データからの情報(尤度)」と「事前の知識(事前分布)」の積で決まります。
- 事前分布:データを観測する前の信念(例:コインの表が出る確率は50%くらいだろう)。
- 尤度:実際に観測したデータがどのパラメータ値を支持するかを示す。
- 事後分布:事前分布と尤度を掛け合わせ、正規化したもの。
下記は図解イメージとなります。
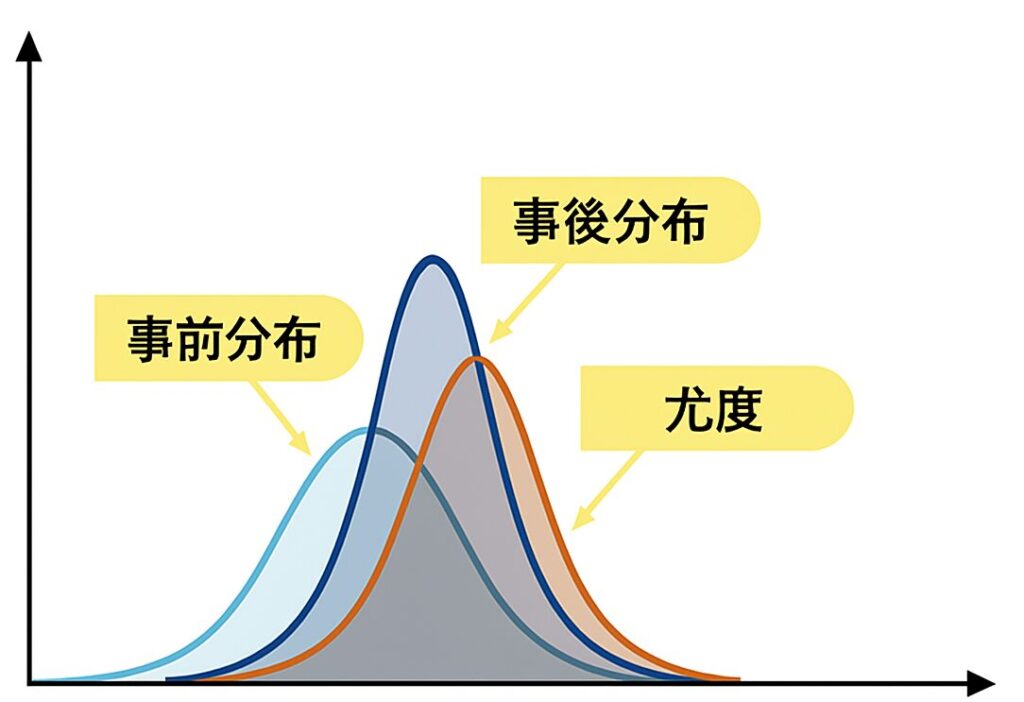
- 事前分布(水色)
データを観測する前の信念を表す。広がった山のような形で、パラメータに対する不確実性が大きい。 - 尤度(オレンジ)
観測データがどのパラメータ値を支持するかを示す。鋭い山のような形で、サンプル平均付近にピークを持つ。 - 事後分布(濃い青)
事前分布と尤度を掛け合わせて正規化したもの。事前分布よりも鋭く、尤度よりもやや広がりを持ち、両者の中間にピークを持つ。
具体例
コイン投げ
コインの表が出る確率を \(\theta\) とします。
10回投げて7回表が出たときの尤度は二項分布に従います:
\[p(x\mid \theta )={10 \choose 7}\theta ^7(1-\theta )^3\]
事前分布としてベータ分布 \(\mathrm{Beta}(\alpha ,\beta ) \)を仮定すると
\[p(\theta )=\frac{1}{B(\alpha ,\beta )}\theta ^{\alpha -1}(1-\theta )^{\beta -1}\]
これを掛け合わせると事後分布は
\[p(\theta \mid x)\propto \theta ^{\alpha +7-1}(1-\theta )^{\beta +3-1}\]
すなわち、
\[p(\theta \mid x)=\mathrm{Beta}(\alpha +7,\beta +3)\]
となります。
正規分布の例
母平均\(\mu\)、母分散cの正規母集団から大きさnの標本を抽出し、標本平均\(\bar{x}\)が得られたします。母平均\(\mu\)の事前分布として期待値\(\mu_{0}\)、分散\(\sigma^{2}_{0}\)の正規分布をとるとき、\(\mu\)の事後分布はどうなるか、みていきましょう。
事前分布は以下のようになります。
\[p(\mu) = \frac{1}{\sqrt{2\pi} \sigma_{0}} exp \left[- \frac{(\mu-\mu_{0})^{2}}{2\sigma^{2}_{0}} \right]\]
次に、正規母集団の密度関数は、
\[f(x) = \frac{1}{\sqrt{2\pi} \sigma} exp \left[-\frac{(x-\mu)^{2}}{2\sigma^{2}} \right]\]
となるため、データ \(D=[x_{1},x_{2},…,x_{n}]\)を得た時、尤度は
$$
\begin{eqnarray}
f(D \mid \mu) &=& \frac{1}{\sqrt{2\pi} \sigma} exp \left[-\frac{(x_{1}-\mu)^{2}}{2\sigma^{2}} \right] \cdot \frac{1}{\sqrt{2\pi} \sigma} exp \left[-\frac{(x_{2}-\mu)^{2}}{2\sigma^{2}} \right] \cdots \frac{1}{\sqrt{2\pi} \sigma} exp \left[-\frac{(x_{n}-\mu)^{2}}{2\sigma^{2}} \right]\\
&=& \left(\frac{1}{\sqrt{2\pi} \sigma}\right)^{n} exp \left[-\frac{(x_{1}-\mu)^{2}}{2\sigma^{2}}-\frac{(x_{2}-\mu)^{2}}{2\sigma^{2}}- \cdots -\frac{(x_{n}-\mu)^{2}}{2\sigma^{2}} \right]
\end{eqnarray}
$$
となります。ここで、expの指数部分は、
$$
\begin{eqnarray}
\text{指数部分} &=& -\frac{1}{2 \sigma^{2}} \left( (x_{1} – \mu)^{2}+(x_{2} – \mu)^{2} + \cdots + (x_{n} – \mu)^{2} \right)\\
&=& -\frac{1}{2 \sigma^{2}} \left( n\mu^{2} -2\mu(x_{1} + x_{2} + \cdots + x_{n}) + (x_{1}^{2} + x_{2}^{2} + \cdots + x_{n}^{2}) \right)\\
&=& -\frac{1}{2 \sigma^{2}} \left( n\left(\mu^{2} – 2\bar{x}\mu \right) + (x_{1}^{2} + x_{2}^{2} + \cdots + x_{n}^{2}) \right)\\
&=& -\frac{1}{2 \sigma^{2}} \left( n(\mu^{2} – 2\bar{x}\mu + \bar{x}^{2}) – n\bar{x}^{2} + (x_{1}^{2} + x_{2}^{2} + \cdots + x_{n}^{2}) \right)\\
&=& -\frac{1}{2 \sigma^{2}} \left( n(\mu – \bar{x})^{2} + \sum_{i=1}^{n}(x_{i}-\bar{x})^{2} \right)\\
&=& -\frac{1}{2 \sigma^{2}} \left( n(\mu – \bar{x})^{2} + nS^{2} \right)
\end{eqnarray}
$$
\[S^{2} = \bar{x}^{2} – (\bar{x})^{2} (S^{2}\text{は標本分散})\]
となります。これを尤度の式に戻すと、
\[f(D \mid \mu) = \left(\frac{1}{\sqrt{2\pi} \sigma}\right)^{n} exp \left[-\frac{n(\mu – \bar{x})^{2} + n S^{2}}{2\sigma^{2}} \right]\]
を得ます。よって、事前分布と尤度を用いて、以下の事後分布を得ます。
\[p(\mu \mid D) = \left( \frac{1}{\sqrt{2\pi}\,\sigma} \right)^{n}
\exp\left[ -\frac{n(\mu – \bar{x})^{2} + n S^{2}}{2\sigma^{2}} \right]
\cdot \frac{1}{\sqrt{2\pi}\,\sigma_{0}} \exp\left[ -\frac{(\mu – \mu_{0})^{2}}{2\sigma_{0}^{2}} \right] \]
P(D)も含めて\(\mu\)に関して、定数とみなせるものを、\(k_{0}\)とおくと、
$$
\begin{eqnarray}
p(\mu \mid D) &=& k_{0} \exp \left[ -\frac{n(\mu – \bar{x})^{2}}{2\sigma^{2}} \right]
\exp \left[ -\frac{(\mu – \mu_{0})^{2}}{2\sigma_{0}^{2}} \right] \
&=& k_{0} \exp \left[ -\frac{n(\mu – \bar{x})^{2}}{2\sigma^{2}}
– \frac{(\mu – \mu_{0})^{2}}{2\sigma_{0}^{2}} \right]
\end{eqnarray}
$$
となります。ここで、指数部分は
$$
\begin{eqnarray}
\text{指数部分} &=& -\frac{n(\mu – \bar{x})^{2}}{2\sigma^{2}} – \frac{(\mu – \mu_{0})^{2}}{2\sigma_{0}^{2}}\\
&=& -\frac{n\sigma_{0}^{2}(\mu – \bar{x})^{2} + \sigma^{2}(\mu – \mu_{0})^{2}}{2\sigma^{2}\sigma_{0}^{2}}\\
&=& -\frac{(n\sigma_{0}^{2} + \sigma^{2})\mu^{2} – 2(n\sigma_{0}^{2}\bar{x} + \sigma^{2}\mu_{0})\mu + (n\sigma_{0}^{2}\bar{x}^{2} + \sigma^{2}\mu_{0}^{2})}{2\sigma^{2}\sigma_{0}^{2}}\\
&=& -\frac{n\sigma_{0}^{2} + \sigma^{2}}{2\sigma_{0}^{2}\sigma^{2}}\left(\mu – \frac{n\sigma_{0}^{2}\bar{x} + \sigma^{2}\mu_{0}}{n\sigma_{0}^{2}+\sigma^{2}} \right)^{2} – \frac{n(\mu_{0} – \bar{x})^{2}}{2(n\sigma_{0}^{2} + \sigma^{2})}
\end{eqnarray}
$$
となります。これを用いて、\(\mu\)に関して定数とみなせるものを\(k_{1}\)とおくと、
\[p(\mu \mid D) = k_{1} exp \left[-\frac{n\sigma_{0}^{2} + \sigma^{2}}{2\sigma_{0}^{2}\sigma^{2}}\left(\mu – \frac{n\sigma_{0}^{2}\bar{x} + \sigma^{2}\mu_{0}}{n\sigma_{0}^{2}+\sigma^{2}} \right)^{2} \right] \]
となります。これは平均\(\frac{n\sigma_{0}^{2}\bar{x} + \sigma^{2}\mu_{0}}{n\sigma_{0}^{2}+\sigma^{2}}\)、分散\(\frac{\sigma_{0}^{2}\sigma^{2}}{n\sigma_{0}^{2} + \sigma^{2}}\)に従う正規分布です。
これより事後分布の平均は、
- \(n \rightarrow \infty \)で、\(\bar{x}\) : 標本が大きいと、標本平均に近づく
- \(\sigma_{0}^{2} \rightarrow \infty \)で、\(\bar{x}\) : 事前分布の分散が大きいと、標本平均に近づく
- \(\sigma_{0}^{2} \rightarrow 0 \)で、\(\mu_{0}\) : 事前分布の分散が小さいと、事前分布の平均に近づく
共役事前分布とは
コイン投げや正規分布の例のように、事前分布と事後分布が同じ分布族に属する場合、その事前分布を 共役事前分布 と呼びます。
| 尤度(データ分布) | 共役事前分布 | 事後分布 |
| 二項分布 | ベータ分布 | ベータ分布 |
| ポアソン分布 | ガンマ分布 | ガンマ分布 |
| 正規分布(平均未知、分散既知) | 正規分布 | 正規分布 |
| 多項分布 | ディリクレ分布 | ディリクレ分布 |
利点:解析的に事後分布を計算できるため、積分を避けられる。
欠点:利用できる分布が限られる。
実務的な意義
小規模データ:事前分布の設定が結果に大きく影響する。
大規模データ:尤度が支配的となり、事前分布の影響は小さくなる。
規制科学(例:医薬品開発):過去の試験データや専門家知見を事前分布に組み込み、限られた臨床試験データを補強できる。
まとめ
ベイズ統計は、事前分布・尤度・事後分布という三つの要素を通じて「信念の更新」を数理的に表現する枠組みです。事前分布はデータを観測する前の知識や仮定を反映し、尤度は観測されたデータがどのパラメータを支持するかを示します。そして事後分布は、両者を統合して得られる更新後の信念であり、データが増えるほど事前分布の影響は薄れ、尤度が支配的になります。
さらに、共役事前分布を選ぶことで、事後分布が事前分布と同じ分布族に属し、解析的に計算が容易になるという利点があります。二項分布とベータ分布、ポアソン分布とガンマ分布、正規分布と正規分布などが代表的な組み合わせです。
図解を通じて、事前分布と尤度の掛け合わせから事後分布が形成される様子を直感的に理解できました。これは「知識とデータの融合」というベイズ統計の本質を示しています。
実務的には、臨床試験や製薬分野など不確実性の高い領域で、過去の知見を事前分布に組み込み、新しいデータで更新することで、より信頼性の高い意思決定を支援できます。ベイズ統計は単なる理論ではなく、現場で活用できる強力なツールであることが確認できました。