ベイズ統計の仮説検定と頻度論的仮説検定の違いを徹底解説
記事の目次
Toggleはじめに
統計的仮説検定は、医薬品開発や臨床試験において欠かせない手法です。従来は頻度論的アプローチが主流でしたが、近年ではベイズ統計の応用が注目されています。特にFDA(米国食品医薬品局)やPMDA(日本医薬品医療機器総合機構)においても、ベイズ的アプローチが現実の規制科学に導入されつつあります。本稿では、頻度論とベイズ統計の仮説検定の違いを整理し、数式・図式・Rコードを交えて解説した上で、FDA/PMDAにおけるベイズ的アプローチの事例を紹介します。
頻度論的仮説検定の基本
頻度論では、パラメータは固定された未知の定数とみなし、確率は「無限回の試行における相対頻度」として解釈されます。
典型的な手順は以下の通りです:
- 帰無仮説 \(H_0\) と 対立仮説 \(H_1\) を設定
- データから統計量(例:平均値)を計算
- p値を算出し、閾値(例:0.05)と比較
- 有意水準以下なら帰無仮説を棄却
例:
\[H_0:\mu =172,\quad H_1:\mu \neq 172\]
標本平均が190cmなら、p値が非常に小さくなり「偶然では説明できない」として H_0 を棄却します。
ベイズ統計的仮説検定の基本
ベイズ統計では、パラメータを確率変数とみなし、事前分布を設定します。データを観測した後、事後分布を更新し、仮説の妥当性を直接評価します。
ベイズの定理
\[p(\theta |D)=\frac{p(D|\theta )\, p(\theta )}{p(D)}\]
仮説検定の方法
データxが得られる確率を、\(\mu\)の値によって評価していきます。データxが与えられた下で、仮説を満たす確率\(P(H_{i}|X)\)が得られます。
例えば、以下のような仮説を考えたとします。
$$
\begin{eqnarray}
\begin{cases}
H_0: & \mu \leq \mu_{0}\\
H_1: & \mu > \mu_{0}
\end{cases}
\end{eqnarray}
$$
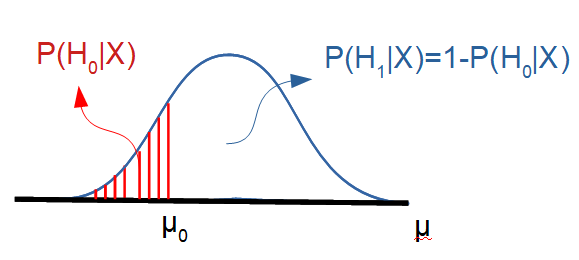
ベイズファクターでの仮説検定
ベイズファクターの定義と数式
ベイズファクターは、データがどちらの仮説をより支持するかを表す比率です。
\[BF_{10}=\frac{p(D|H_1)}{p(D|H_0)}\]
ここで:
- p(D|H_1):対立仮説の下での周辺尤度
- p(D|H_0):帰無仮説の下での周辺尤度
事後オッズ比は次のように表されます:
\[\frac{P(H_1|D)}{P(H_0|D)}=BF_{10}\cdot \frac{P(H_1)}{P(H_0)}\]
つまり、ベイズファクターは事前オッズを事後オッズに更新する倍率です。
ベイズファクターの解釈基準(Jeffreysの尺度)
ジェフリーズはベイズファクターの大きさで、証拠価値を以下のように表現しています。
| \(BF_{10}\) | \(H_0 vs H_1\)で\(H_0\)に有利な証拠の強さ |
| 1~3.2 | コメントする程度で十分 |
| 3.2~10 | ある程度 |
| 10~32 | 強い |
| 32~100 | 非常に強い |
| >100 | 決定的 |
p値とベイズファクターの違い
- p値:\(H_0\)を仮定してデータの稀さを評価
- ベイズファクター:\(H_0 \, , H_1 \)の両方を考慮して、データの尤度比で評価
頻度論 vs ベイズ統計を図解で表現
今までの内容を図解で表現すると下記のようになります。
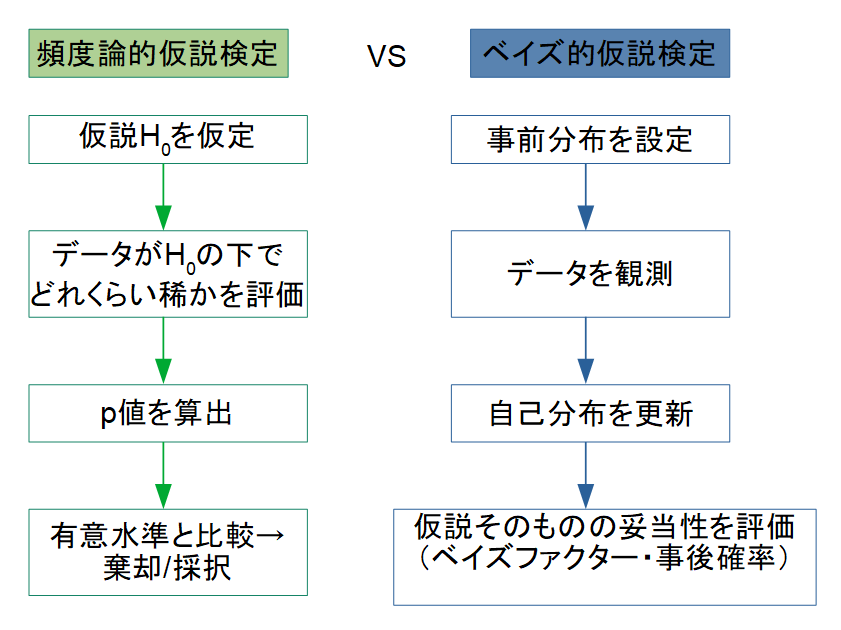
Rによる実装例
頻度論的t検定
set.seed(123)
data <- rnorm(30, mean = 175, sd = 10)
t.test(data, mu = 172)

解釈:p値が0.1686のため、帰無仮説をacceptします。
ベイズファクターによるt検定
library(BayesFactor)
bf <- ttestBF(x = data, mu = 172)
bf
Bayes factor analysis
[1] Alt., r=0.707 : 1.45
解釈: \(BF_{10}\)=1.45:弱い証拠で対立仮説を支持。
FDA/PMDAにおけるベイズ的アプローチの事例
FDA
- 医療機器審査:「Bayesian Guidance for Medical Device Clinical Trials (2010)」で公式にベイズ的試験デザインを承認。
- 適応的デザイン:中間解析で試験を柔軟に変更可能。
PMDA
- 希少疾患治療薬:海外データを事前分布に組み込み、日本での小規模試験と統合。
- RWD活用:リアルワールドデータを事前情報として利用するベイズ的解析を検討中。
まとめ
統計的仮説検定には、頻度論的アプローチとベイズ的アプローチという二つの大きな枠組みがあります。頻度論では「データが帰無仮説の下でどれくらい稀か」を評価し、p値を基準に仮説を棄却するかどうかを判断します。一方、ベイズ統計では「仮説そのものがデータを踏まえてどれくらい妥当か」を評価し、事前分布と事後分布を用いて仮説の確からしさを直接比較します。
特にベイズファクターは、データがどちらの仮説をより支持するかを定量化する指標であり、Jeffreysの尺度によって証拠の強さを解釈できます。これにより、単なる「有意/非有意」の二分法ではなく、仮説間の相対的な支持度を柔軟に評価できる点が大きな利点です。
実務的には、頻度論は依然として規制当局で標準的に用いられていますが、FDAやPMDAではベイズ的アプローチが導入されつつあります。特に希少疾患や医療機器の審査において、事前情報やリアルワールドデータを活用することで、少数例でも科学的に妥当な判断が可能となっています。
したがって、頻度論とベイズ統計は対立するものではなく、目的や状況に応じて使い分けるべき補完的な手法です。頻度論の「データの稀さ」とベイズ統計の「仮説の妥当性」を理解し、両者を適切に活用することが、現代の医薬品開発や規制科学において重要な戦略となります。