ベイズ統計の信用区間と頻度論の信頼区間の違いについて
記事の目次
Toggleはじめに
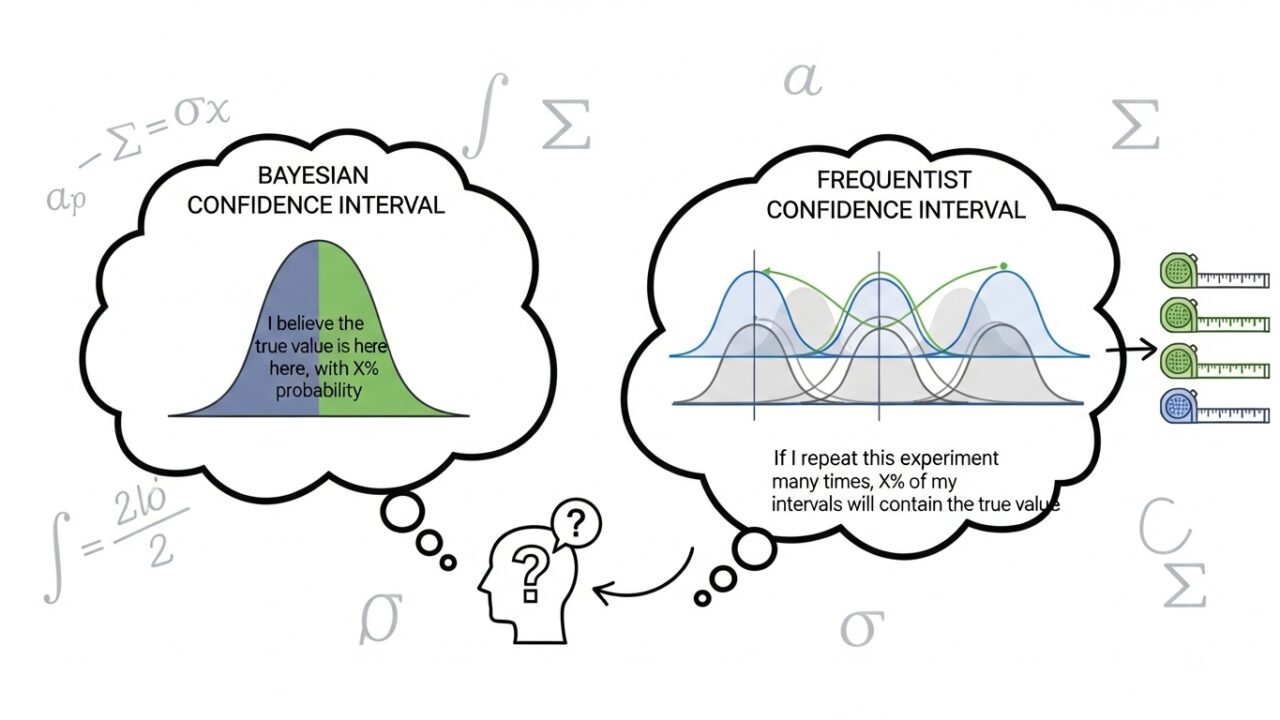
統計学において「区間推定」は、未知の母数に対する不確実性を表現する重要な手法です。頻度論的アプローチでは「信頼区間」、ベイズ的アプローチでは「信用区間」という異なる概念が用いられます。両者は似たような形で「範囲」を提示しますが、背後にある解釈が根本的に異なるため、混同すると誤解を招きます。
そこで今回は信用区間と信頼区間の違いについて解説し、R言語による実装例も用いて解説していきます。
頻度論の信頼区間
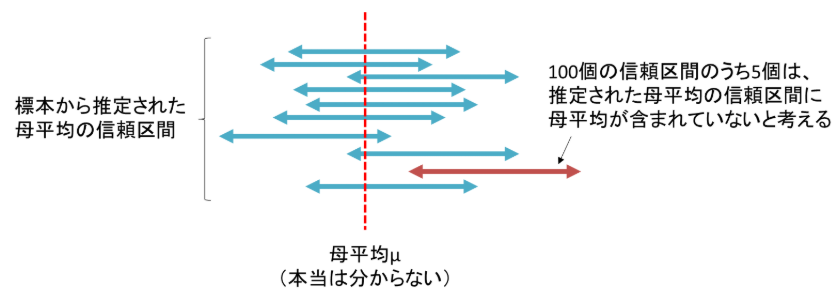
頻度論では、母数は固定された未知の値とみなし、データはランダムに変動するものと考えます。信頼区間は「多数の標本を繰り返し抽出したとき、そのうち一定割合の区間が真の母数を含む」という性質を持ちます。
数式表現
母平均 \(\mu\) を推定する場合、標本平均 \(\bar {X}\) の標準誤差を用いて次のように表されます。
\[CI_{95\% }=\bar {X}\pm z_{0.025}\cdot \frac{\sigma }{\sqrt{n}}\]
ここで、\(z_{0.025}\) は標準正規分布の上側2.5%点です。
- 「この区間が95%の確率で母数を含む」とは言えない
- 正しい解釈は「無限に標本を繰り返したとき、95%の区間が母数を含む」というもの。
https://bellcurve.jp/statistics/course/8891.html
ベイズ統計の信用区間
ベイズ統計では、母数そのものを確率変数とみなし、データと事前分布を組み合わせて事後分布を得ます。信用区間は、この事後分布に基づき「母数がある範囲に含まれる確率」を直接表現します。
数式表現
事後分布 \(\pi (\theta |x)\) に基づく信用区間は次のように定義されます。
\[P\left( \theta \in [a,b]\mid x\right) =0.95\]
つまり、「母数 \(\theta\) が区間 [a,b] に含まれる確率が95%」という直感的な解釈が可能です。
言い換えると、事後分布の分布の中で、「確率が95%を含む範囲」といえます。
- 等裾信用区間(Equal-tailed interval)
事後分布の両端を同じ確率で切り落とす。 - 最高事後密度区間(HPD: Highest Posterior Density interval)
事後分布の密度が最も高い領域を選ぶ。
HPD区間と等裾区間の違いを深掘り
定義の違い
等裾区間(Equal-tailed Interval):
事後分布の両端を同じ確率(例:2.5%ずつ)で切り落とし、残りの95%を含む区間。
数式で表すと、
\[P(\theta < a \mid x) = \alpha /2 , P(\theta > b\mid x)=\alpha /2\]
となる区間 \([a,b]\)のことです。
HPD区間(Highest Posterior Density Interval):
事後分布の密度が最も高い部分を選び、全体で95%の確率質量を含む区間。
数式で表すと以下のようになります。
\[\pi (\theta \mid x)\geq k\quad \mathrm{となる集合Cで\ }P(\theta \in C\mid x)=0.95\]
図解イメージ
下記で2つの分布の場合を見ていきます。
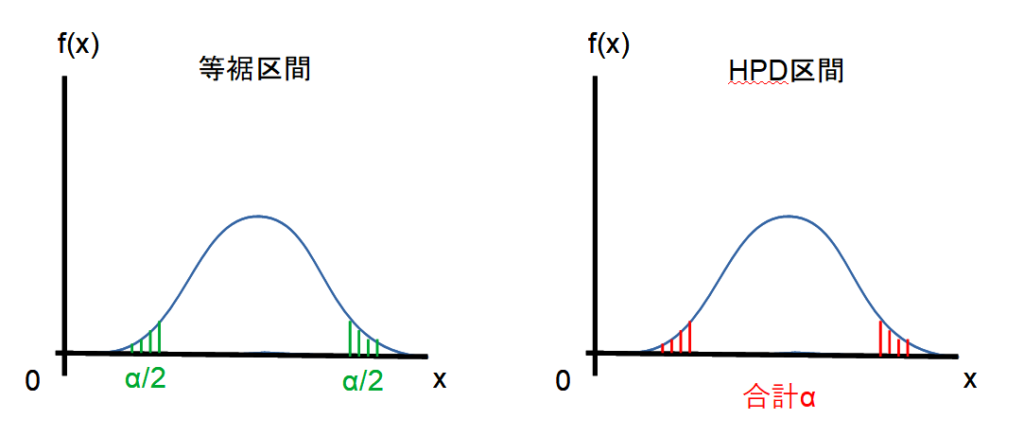
正規分布(対称分布):等裾区間とHPD区間はほぼ同じ。
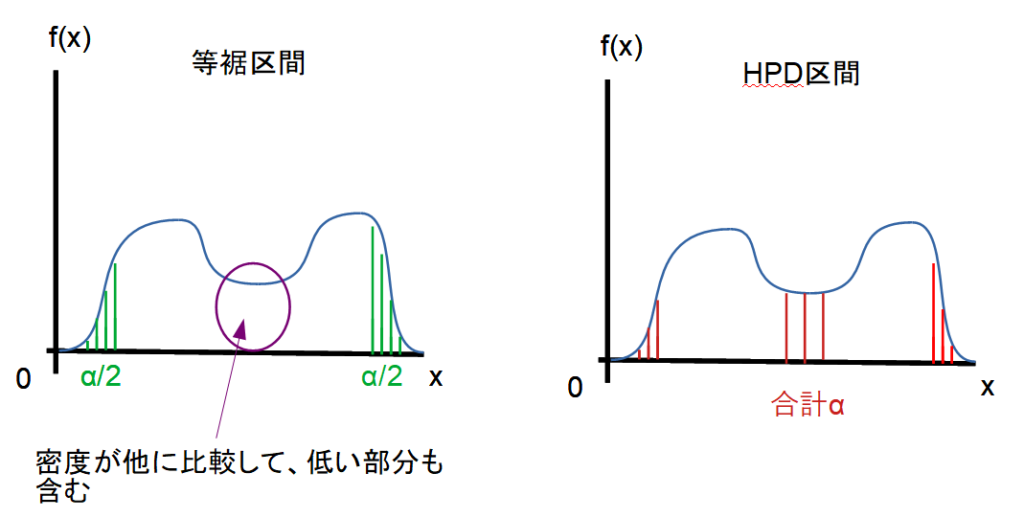
密度が異なる分布:密度が異なる分布では、HPD区間では、密度が高い部分を選び、区間とします。そのため、パラメータの真値である可能性が高い区間という意味でHPD区間のほうが、適切を考えられます。
Rによる実装例
頻度論的信頼区間
# データ生成
set.seed(123)
x <- rnorm(100, mean = 5, sd = 2)
# 標本平均と標準誤差
mean_x <- mean(x)
se_x <- sd(x) / sqrt(length(x))
# 95%信頼区間
ci_lower <- mean_x – qnorm(0.975) * se_x
ci_upper <- mean_x + qnorm(0.975) * se_x
c(ci_lower, ci_upper)

ベイズ的信用区間(単純な正規事前分布)
library(rstanarm)
# データ生成
set.seed(123)
x <- rnorm(100, mean = 5, sd = 2)
# ベイズ回帰で平均を推定
fit <- stan_glm(x ~ 1, prior = normal(0, 10), chains = 2, iter = 2000)
# 95%信用区間の取得
posterior_interval(fit, prob = 0.95)
例えば結果が [4.7, 5.3] と出た場合:
- 解釈は「母平均がこの区間に含まれる確率が95%」と直接言えます。
- これは事後分布に基づく確率的な推定であり、直感的に理解しやすいです。
- 規制科学や製薬分野では「母数がこの範囲にある確率」を明示できる点が、意思決定に有用となります。
まとめ
今回はベイズ統計の信用区間と頻度論の信頼区間の違いについて解説いたしました。
区間推定における頻度論とベイズ統計の違いは、母数の扱い方と区間の解釈に根本的な差があります。頻度論的な信頼区間は「推定方法の性質」を保証するものであり、無限に標本を繰り返したときに一定割合の区間が真の母数を含むことを意味します。一方で、ベイズ的な信用区間は事後分布に基づき「母数がその区間に含まれる確率」を直接表現できるため、より直感的で意思決定に活用しやすい特徴があります。
さらに、信用区間には等裾区間と HPD 区間という二つの代表的な形式があります。対称的な分布では両者はほぼ同じですが、分布が歪んでいる場合には HPD 区間の方が短く、事後分布の密度が高い領域を優先して示すため、より「確からしい」範囲を提示できます。実務では、標準的な報告には等裾区間を用い、歪んだ分布や多峰性分布では HPD 区間を選ぶことで、より適切な解釈が可能となります。
このように、信頼区間と信用区間の違いを理解し、状況に応じて等裾区間と HPD 区間を使い分けることは、医薬品開発や規制科学における統計的意思決定をより確かなものにする重要なステップです。