ベイズ統計を用いたサンプルサイズ設定~頻度論の方法との比較も交えて~

記事の目次
Toggleはじめに
臨床試験や製薬研究において、サンプルサイズの設定は研究計画の根幹を成す要素です。サンプルサイズが小さすぎれば統計的な不確実性が大きくなり、結論の信頼性が損なわれます。一方で過剰に大きなサンプルサイズはコストや倫理的負担を増大させます。従来は頻度論的な枠組みで「検出力(power)」や「有意水準(α)」を基準にサンプルサイズを決定することが一般的でした。しかし近年、ベイズ統計の普及に伴い、事前分布や事後分布を活用した柔軟なサンプルサイズ設定法が注目されています。
本稿では、頻度論的手法とベイズ的手法の違いを整理しつつ、ベイズ統計に基づくサンプルサイズ設定の考え方を数理的に解説します。
ベイズ統計と頻度論の違いは下記で解説にしているので、是非ご一読ください。

頻度論的サンプルサイズ設定の基本
頻度論では、サンプルサイズ n は以下の要素によって決定されます。
- 有意水準(α): 第一種過誤(偽陽性)の許容確率
- 検出力(1−β): 対立仮説が真のときに帰無仮説を正しく棄却できる確率
- 効果量(Δ): 群間差や推定したいパラメータの大きさ
- 分散(σ²): データのばらつき
例えば、2群の平均差を検出するためのサンプルサイズは次式で近似されます。
\[n=\frac{2\sigma ^2(z_{1-\alpha /2}+z_{1-\beta })^2}{\Delta ^2}\]
ここで\( z_p\) は標準正規分布の p 分位点です。
この枠組みでは「もし帰無仮説が真であれば…」「もし効果量がΔであれば…」という仮定のもとで、長期的な誤差率を制御することが目的となります。
ベイズ統計におけるサンプルサイズ設定の考え方
ベイズ統計では、確率は「長期的頻度」ではなく「信念の度合い」を表します。したがってサンプルサイズ設定も「事後分布がどの程度の精度を持つか」「意思決定に十分な確率的保証が得られるか」という観点で行われます。
事後分布の精度に基づく設定
あるパラメータ \(\theta\) の推定に関心があるとします。観測データ y に基づく事後分布は
\[p(\theta \mid y)\propto p(y\mid \theta )\, p(\theta )\]
で与えられます。サンプルサイズ n を増やすと尤度 p(y\mid \theta ) が鋭くなり、事後分布の分散が縮小します。
例えば、正規分布モデル \(y_i\sim N(\theta ,\sigma ^2\)) を考えると、共役事前分布として \(\theta \sim N(\mu _0,\tau _0^2)\) を置いた場合、事後分布は
\[\theta \mid y\sim N\left( \frac{\frac{n}{\sigma ^2}\bar {y}+\frac{1}{\tau _0^2}\mu _0}{\frac{n}{\sigma ^2}+\frac{1}{\tau _0^2}},\; \frac{1}{\frac{n}{\sigma ^2}+\frac{1}{\tau _0^2}}\right)\]
となります。ここで事後分散は
\[\mathrm{Var}(\theta \mid y)=\frac{1}{\frac{n}{\sigma ^2}+\frac{1}{\tau _0^2}}\]
であり、サンプルサイズ n が大きくなるほど分散は小さくなります。したがって「事後分布の幅が十分に狭くなるように n を選ぶ」という基準が考えられます。
ベイズ的意思決定に基づく設定
ベイズ統計では「ある仮説がどの程度の確率で支持されるか」を直接評価できます。例えば「治療効果 \(\Delta\) が 0 より大きい確率が 95%以上である」という条件を満たすためのサンプルサイズを設定することが可能です。
形式的には、
\[\Pr (\theta >0\mid y)\geq 0.95\]
を満たすために必要な n をシミュレーションで探索します。これは頻度論的な「p値が0.05未満」という基準とは異なり、直接的に「効果がある確率」を評価する点で解釈が明快です。
期待効用に基づく設定
さらにベイズ的枠組みでは「期待効用」を最大化する観点からサンプルサイズを決定できます。例えば、試験のコストを C(n)、正しい意思決定による利益を\( U(\theta )\) とすると、期待効用は
\[EU(n)=\mathbb{E}[U(\theta )\mid y]-C(n)\]
で表されます。最適なサンプルサイズは
\[n^*=\arg \max _nEU(n)\]
として定義されます。これは頻度論的な「誤差率の制御」とは異なり、意思決定の価値を直接考慮できる点で実務的に有用です。
頻度論とベイズの違いのまとめ
| 観点 | 頻度論 | ベイズ統計 |
| 基準 | α, β, 検出力 | 事後分布の確率、精度、期待効用 |
| 解釈 | 長期的誤差率の制御 | 効果の確率的保証、意思決定の価値 |
| 数式例 | \(n=\frac{2\sigma ^2(z_{1-\alpha /2}+z_{1-\beta })^2}{\Delta ^2}\) | \(\Pr (\theta >0\mid y)\geq 0.95\) を満たす n |
| 実務的利点 | 標準化されており規制当局に馴染み深い | 柔軟で直感的、事前情報やコストを反映可能 |
具体例:2群の平均差を検出する場合のサンプルサイズ設定
設定
- 目的:新薬群と対照群の平均血圧低下量の差を検出する
- 想定効果量:\(\Delta =5\) mmHg
- 標準偏差:\(\sigma =10\) mmHg
- 有意水準:\(\alpha =0.05\)
- 検出力:1-\(\beta\) =0.8
- 事前分布(ベイズ):効果量 \(\theta\) に対して \(\theta \sim N(0,\tau _0^2)\)、ここでは \(\tau _0^2=25\) と仮定
頻度論的サンプルサイズ計算
2群の平均差を検出するためのサンプルサイズ公式は以下です。
\[n=\frac{2\sigma ^2(z_{1-\alpha /2}+z_{1-\beta })^2}{\Delta ^2}\]
ここで
- \(z_{1-\alpha /2}=1.96\)
- \(z_{1-\beta }=0.84\)
代入すると:
\[n=\frac{2\cdot 100\cdot (1.96+0.84)^2}{25}=\frac{200\cdot (2.8)^2}{25}=\frac{200\cdot 7.84}{25}=\frac{1568}{25}=62.7\]
したがって、各群63例程度が必要と算出されます。
ベイズ的サンプルサイズ計算
ベイズ的には「効果量が0より大きい確率が95%以上となる」ことを基準にします。
事後分布は以下の形になります。
\[\theta \mid y\sim N\left( \frac{\frac{n}{\sigma ^2}\bar {y}+\frac{1}{\tau _0^2}\mu _0}{\frac{n}{\sigma ^2}+\frac{1}{\tau _0^2}},\; \frac{1}{\frac{n}{\sigma ^2}+\frac{1}{\tau _0^2}}\right)\]
ここで事前平均 \(\mu _0=0\)、事前分散 \(\tau _0^2=25\)。
事後分散は:
\[\mathrm{Var}(\theta \mid y)=\frac{1}{\frac{n}{100}+\frac{1}{25}}\]
例えば、効果量が真に\( \Delta =5\) であると仮定すると、事後平均はおおよそ \(\bar {y}=5\) に近づきます。
「効果が正である確率が95%以上」とは、
\[\Pr (\theta >0\mid y)\geq 0.95\]
すなわち、事後平均が事後標準偏差の約1.645倍以上であることを意味します。
これは、正規分布の片側検定における臨界値 \(Z_{0.05}=1.645\)であり、事後分布が正規分布に従うと仮定したときに、平均値がゼロからどれだけ離れているかを「事後標準偏差」で割った値(=Zスコア)が 1.645以上 であれば、ゼロより大きい確率が95%以上になる、という意味です。
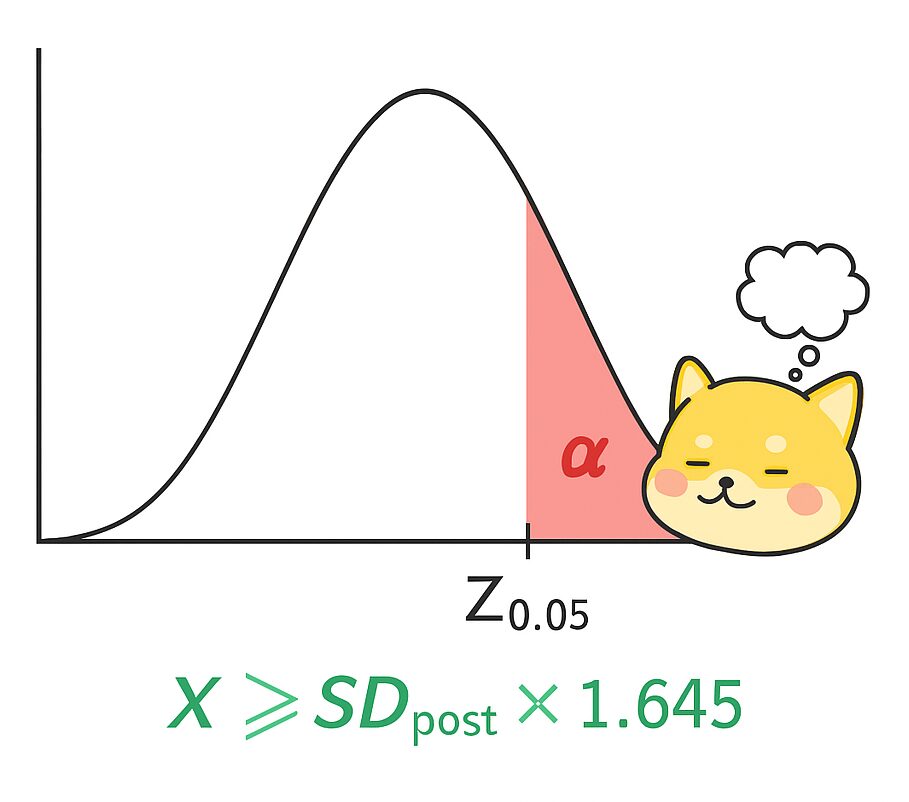
事後標準偏差は
\[\sqrt{\frac{1}{\frac{n}{100}+\frac{1}{25}}}\]
です。これが 5 / 1.645 以下になるように n を選びます。
計算すると:
\[\sqrt{\frac{1}{\frac{n}{100}+0.04}}\leq 3.04\]
両辺を二乗して整理すると:
\(\frac{1}{\frac{n}{100}+0.04}\leq 9.24\)
\(\frac{n}{100}+0.04\geq 0.108\)
\(\frac{n}{100}\geq 0.068\)
\(n\geq 6.8\)
したがって、各群7例程度で十分という結果になります。
結果の比較&解釈
| 方法 | 必要サンプルサイズ(各群) | 根拠 |
| 頻度論 | 約63例 | 有意水準と検出力に基づく誤差率制御 |
| ベイズ | 約7例 | 事後分布で「効果が正である確率 ≥ 95%」を保証 |
- 頻度論では「長期的な誤差率の制御」が目的であるため、サンプルサイズは大きく算出されます。
- ベイズでは「事後分布に基づく確率的保証」が目的であり、事前情報を活用することで必要サンプルサイズが大幅に小さくなることがあります。
- 特に希少疾患試験などでは、ベイズ的アプローチが現実的な選択肢となり得ます。
規制当局の視点
- FDAやPMDAは、頻度論的枠組みを基本としつつも、希少疾患や小児試験ではベイズ的アプローチを認めるケースが増えています。
- 特に「事前情報の活用」「事後分布に基づく確率的保証」「適応的デザイン」は、倫理的・実務的に合理的と評価されやすいです。
- ただし、事前分布の設定根拠を明確に示すこと、感度分析を行うことが必須です。
まとめ
ベイズ統計によるサンプルサイズ設定は、事後分布に基づく確率的保証や期待効用の最大化を基準とするため、頻度論とは異なる柔軟な設計が可能です。特に希少疾患や小児試験など、症例数が限られる領域では、事前情報を活用することで少数例でも有意な判断が可能となります。頻度論が誤差率の制御を重視するのに対し、ベイズは意思決定の質を重視するため、今後の臨床試験設計において重要性が高まると期待されます。