はじめに
統計解析において「複数の群の平均値を比較する」場面は非常に多い。例えば、ある薬剤の効果を3種類の投与群で比較したい場合、単純にt検定を繰り返すと多重比較の問題が生じ、誤った結論を導く危険がある。そこで用いられるのが一元配置分散分析（one-way ANOVA）である。本記事では、数理的な導入からR言語での実装までを体系的に解説する。
基本的な考え方
一元配置分散分析は、1つの要因（factor）に基づいて複数の群に分けられたデータの平均値に差があるかを検定する方法である。
- 帰無仮説 \(H_0\)：すべての群の母平均は等しい
- 対立仮説 \(H_1\)：少なくとも1つの群の母平均が異なる
例：3群（A, B, C）の平均値を比較する場合、
\[H_0: \mu_A = \mu_B = \mu_C\]
\[H_1: \text{少なくとも1つの群の平均が異なる}\]
数理的導入
データの定義
観測値を\(Y_{ij}\)とする。ここで、
- \(i = 1, 2, \dots, k：\)群のインデックス（群数 = k）
- \(j = 1, 2, \dots, n_i：\)群内の観測番号
| 分布 | |||||||
| \(A_{1}\) | \(Y_{11}\) | \(Y_{12}\) | \(\cdots\) | \(Y_{1n_{1}}\) | \(~N(\mu_{1}, \sigma^{2})\) | ||
| \(A_{2}\) | \(Y_{21}\) | \(Y_{22}\) | \(\cdots\) | \(Y_{2n_{2}}\) | \(~N(\mu_{2}, \sigma^{2})\) | ||
| \(\vdots\) | |||||||
| \(A_{i}\) | \(Y_{i1}\) | \(Y_{i2}\) | \(\cdots\) | \(Y_{ij}\) | \(\cdots\) | \(Y_{in_{i}}\) | \(~N(\mu_{i}, \sigma^{2})\) |
| \(\vdots\) | |||||||
| \(A_{k}\) | \(Y_{k1}\) | \(Y_{k2}\) | \(\cdots\) | \(Y_{kn_{k}}\) | \(~N(\mu_{k}, \sigma^{2})\) |
この時モデルは以下のように表すことができる。
\[Y_{ij} = \mu + \alpha_i + \varepsilon_{ij}\]
- \(\mu\)：全体平均（grand mean）
- \(\alpha_i\)：群 i の効果（群平均のずれ）
- \(\varepsilon_{ij}\)：誤差項（独立同分布 \(N(0, \sigma^2)\) を仮定）
制約条件として \(\sum_{i=1}^k \alpha_i = 0\) を課す。
仮説
仮説は以下のように設定する。
- \(H_0 : \mu_1 = \mu_2 = \cdots = \mu_k (= \mu)\)
- \(H_1 : not H_0 \text{少なくとも1ヵ所は等号が成立しない}\)
一元配置分散分析の数理的導入
一元配置分散分析の数理的導入のために、定理
以下の定理を証明していく。
\(H_0\)の下での\(\mu\)と\(\sigma^2\)の最尤推定値は以下のようになる。
\[\hat{\mu} = \frac{1}{N}\sum_{i=1}^{k}\sum_{j=1}^{n_{i}}Y_ij (\equiv \bar{Y}_{..})\]
\[\hat{\sigma}^2 = \frac{1}{N}\sum_{i=1}^{k}\sum_{j=1}^{n_{i}}(Y_{ij} – \bar{Y}_{..})\]
ただし、\(N =n_1 + n_2 + \cdots + n_{k}\)
(証明)
\(Y_{ij}\)の確率密度関数は、\(N(\mu_{i}, \sigma^{2})\)に従うことから、
\[f(y_{ij}) = \frac{1}{\sqrt{-2\pi\sigma^2}}e^{-\frac{1}{2\sigma^2}(y_{ij} – \mu_i)^2}\]
こちらの尤度関数は、
\[L = \prod_{i=1}^{k}\prod_{j=1}^{n_i}\frac{1}{\sqrt{-2\pi\sigma^2}}e^{-\frac{1}{2\sigma^2}(y_{ij} – \mu_i)^2}\]
尤度関数を対数をとった、対数尤度関数は
\[logL =-\frac{N}{2}log(2\pi) – \frac{N}{2}log(\sigma^2) – \frac{1}{2\sigma^2}\sum_{i=1}^{k}\sum_{j=1}^{n_i}(y_{ij} – \mu_i)^2\]
それぞれ、\(\mu_i,\sigma^2\)で微分すると、
\[\frac{\partial logL}{\partial \mu_i} = \frac{1}{\sigma^2}\sum_{j=1}^{n_i}(y_{ij} – \mu_i) (\equiv 0)\]
\[\frac{\partial logL}{\partial \sigma^2} = – \frac{N}{2\sigma^2} – \frac{1}{2(\sigma^2)^2}\sum_{i=1}^{k}\sum_{j=1}^{n_i}(y_{ij} – \mu_i)^2 (\equiv 0)\]
上記２式より、\(\hat{\mu_i},\hat{\sigma}^2\)を解くと、
\[\hat{\mu_i} = \frac{1}{n_i}\sum_{j=1}^{n_i}Y_{ij} (\equiv \bar{Y}_{i.}) \]
\[\hat{\sigma}^{2} = \frac{1}{N}\sum_{i=1}^{k}\sum_{j=1}^{n_i}(Y_{ij} – \bar{Y}_{i.})^2\]
よって、
\[\hat{\mu} = \frac{1}{N}\sum_{i=1}^{k}\sum_{j=1}^{n_i}Y_{ij} (\equiv \bar{Y}_{..}) \]
\[\hat{\sigma}^{2} = \frac{1}{N}\sum_{i=1}^{k}\sum_{j=1}^{n_i}(Y_{ij} – \bar{Y}_{..})^2\]
\[N\hat{\sigma}^2 = N\hat{\sigma}^2 + \sum_{i=1}^{k}n_{i}(\hat{\mu_i} – \hat{\mu})^2\]
\[\leftrightarrow \sum_{i=1}^{k}\sum_{j=1}^{n_i}(Y_{ij} – \bar{Y}_{..})^2 = \sum_{i=1}^{k}\sum_{j=1}^{n_i}(Y_{ij} – \bar{Y}_{i.})^2 + \sum_{i=1}^{k}\sum_{j=1}^{n_i}(Y_{i.} – \bar{Y}_{..})^2\]
ここで、
\[S_r\text{全変動}:\sum_{i=1}^{k}\sum_{j=1}^{n_i}(Y_{ij} – \bar{Y}_{..})^2\]
\[S_e\text{級内(誤差)変動}:\sum_{i=1}^{k}\sum_{j=1}^{n_i}(Y_{ij} – \bar{Y}_{i.})^2\]
\[S_B\text{級間変動}:\sum_{i=1}^{k}\sum_{j=1}^{n_i}(Y_{i.} – \bar{Y}_{..})^2\]
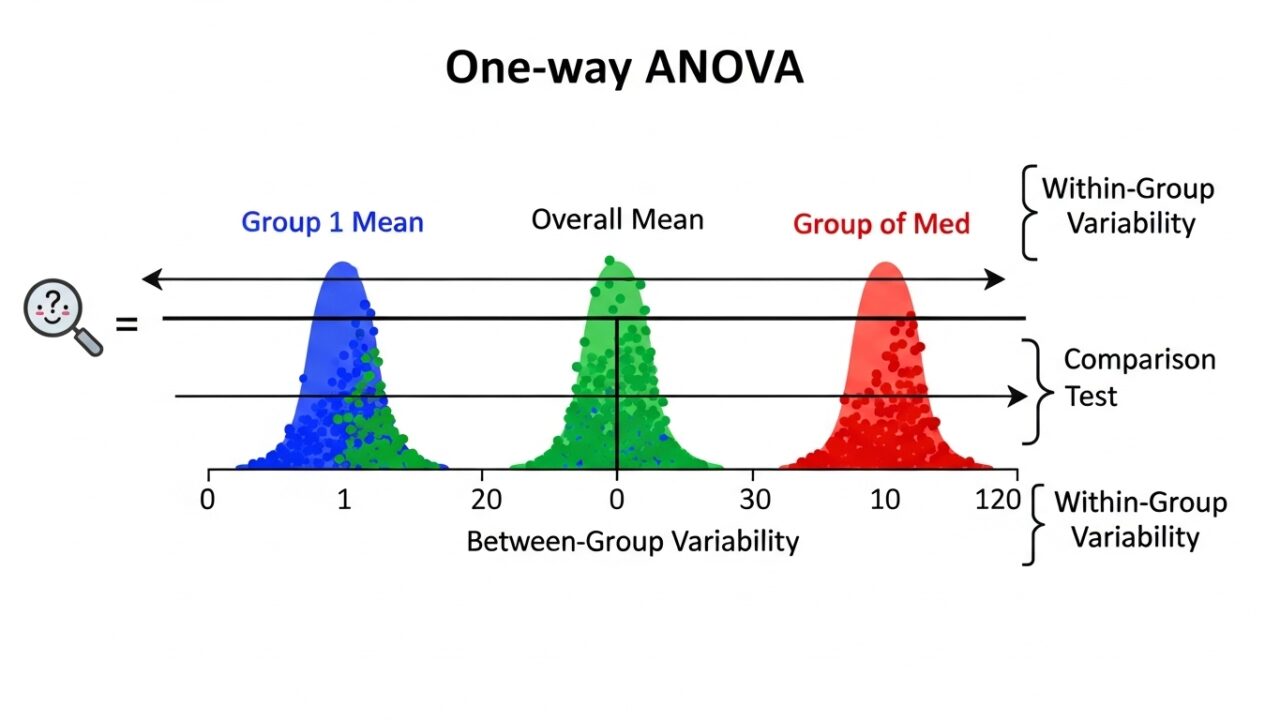
- 全変動は個々の値(\(Y_{ij}\))と\(\bar{Y}_{..}\)を比べている
- 級内変動は個々の値(\(Y_{ij}\))と\(\bar{Y}_{i.}\)を比べている
- 級間変動は群の平均と\(\bar{Y}_{..}\)と比べている
\[E(S_e) = (N – k)\sigma^2\]
\[E(S_B) = (k -1)\sigma^2 + \sum_{i=1}^{k}n_i(\bar{\mu} – \mu_i)^2\]
※\(\bar{\mu} = \frac{1}{N}\sum_{i=1}^{k}n_i\mu_i (=E(\bar{X}_{..}) )\)
また、\(H_0\)の下では、\(\bar{\mu} = \mu\)となるので、
\[E(S_B) = (k – 1)\sigma^2\]
証明
\(E(S_e) = (N – k)\sigma^2\)についてのみ証明する。
$$
\begin{eqnarray}
S_e &=& \sum_{i=1}^{k}\sum_{j=1}^{n_i}(Y_{ij} – \bar{Y}_{i.})^2\\
&=& \sum_{i=1}^{k}\sum_{j=1}^{n_i} \left[(Y_{ij} – \mu_i) – (\bar{Y}_{i.} – \mu_i)\right]^2\\
&=& \sum_{i=1}^{k}\sum_{j=1}^{n_i} (Y_{ij} – \mu_i)^2 – 2 \sum_{i=1}^{k} (\bar{Y}_{i.} – \mu_i) \sum_{j=1}^{n_i}(Y_{ij} – \mu_i) + \sum_{i=1}^{k} n_i (\bar{Y}_{i.} – \mu_i)^2\\
&=& \sum_{i=1}^{k}\sum_{j=1}^{n_i} (Y_{ij} – \mu_i)^2 – \sum_{i=1}^{k} n_i (\bar{Y}_{i.} – \mu_i)^2
\end{eqnarray}
$$
$$
\begin{eqnarray}
E(Se) &=& \sum_{i=1}^{k}\sum_{j=1}^{n_i} E[(Y_{ij} – \mu_i)^2] – \sum_{i=1}^{k}n_iE[(\bar{Y}_{i.} – \mu_i)^2]\\
&=& N\sigma^2 – k\sigma^2\\
&=& (N – k)\sigma^2
\end{eqnarray}
$$
- \[\frac{1}{\sigma^2}S_e ~ \chi^2_{(N-k)}\]
- \[\frac{1}{\sigma^2}S_B ~ \chi^2_{(k-1)} (H_0\text{の下で})\]
- \(S_e\)と\(S_B\)は独立
証明
\[Z_i = \frac{1}{\sigma^2}\sum_{j=1}^{n_i}(Y_{ij} – \bar{Y}_{i.})^2 \sim \chi^2_{(n_i-1)}\]
\(\chi^2\)分布の加法性より、
\[Z_1 + \cdots + Z_k \sim \chi^2_{\sum_{i=1}^{k}n_i-1} = \chi^2_{(N – k)}\]
ここで、定理4より、\(H_0\)の下では検定統計量Fは以下のようになる。
\[F = \frac{\frac{1}{k-1}\frac{1}{\sigma^2}S_B}{\frac{1}{N-k}\frac{1}{\sigma^2}S_e} = \frac{N-k}{k-1}\frac{S_B}{S_e} \sim F^{(k-1)}_{(N-k)}\]
このFを用いて検定を行うのが一元配置分散分析です。
一元配置分散分析の前提条件
ANOVAを適用するには以下の前提がある。
- 独立性：各観測は独立である
- 正規性：各群の誤差分布は正規分布に従う
- 等分散性：各群の分散は等しい
これらが大きく崩れる場合は、WelchのANOVAやノンパラメトリック検定（Kruskal-Wallis検定）を検討する。
R言語の実装例
架空のデータとして、3種類の薬剤群（A, B, C）の血圧低下量を比較する。
set.seed(123)
group <- rep(c(“A”, “B”, “C”), each = 10)
value <- c(rnorm(10, mean = 5, sd = 2),
rnorm(10, mean = 7, sd = 2),
rnorm(10, mean = 6, sd = 2))
data <- data.frame(group, value)
head(data)
anova_model <- aov(value ~ group, data = data)
summary(anova_model)
Df Sum Sq Mean Sq F value Pr(>F) group 2 20.35 10.175 3.45 0.048 *
Residuals 27 79.65 2.950
解釈：p値が0.05未満であるので、「群間に有意差あり」と結論する。
有意差が見られた場合、どの群間に差があるかを調べるために多重比較を行う。
TukeyHSD(anova_model)
Tukey multiple comparisons of means
95% family-wise confidence level
Fit: aov(formula = value ~ group, data = data)
$group
diff lwr upr p adj
B-A 2.10 0.05 4.15 0.045
C-A 1.05 -0.99 3.09 0.310
C-B -1.05 -3.09 0.99 0.310
解釈:この結果から、群Aと群Bの間に有意差があることが分かる。
まとめ
今回は一元配置分散分析について解説いたしました。一元配置分散分析（one-way ANOVA）は、1つの要因に基づいて複数の群の平均値を比較するための基本的かつ強力な統計手法である。その本質は、データ全体の変動を「群間の変動」と「群内の変動」に分解し、それらの比率をF統計量として評価する点にあります。帰無仮説の下では、このF値は理論的にF分布に従うため、群間に有意な差が存在するかどうかを形式的に検定できます。実務においては、まずANOVAで全体的な差の有無を確認し、有意差が認められた場合には多重比較を行って具体的にどの群間に差があるのかを明らかにすることが重要です。また、適用にあたっては「独立性」「正規性」「等分散性」という前提条件を確認する必要があり、これらが大きく崩れる場合にはWelchのANOVAやノンパラメトリック検定といった代替手法を検討すべきです。
