中間解析におけるα消費関数法の解説
記事の目次
Toggleはじめに
臨床試験において「中間解析(interim analysis)」は、試験途中でデータを評価し、早期に有効性や安全性を判断するための重要な手法です。しかし、中間解析を行うと「多重検定」の問題が生じ、第一種過誤(Type I error, 偽陽性)の確率が増加してしまいます。これを制御するために考案されたのが α消費関数法(α-spending function approach) です。本記事では、α消費関数法の数理的背景、代表的な関数の種類、実際の臨床試験での応用例、Rコードによるシミュレーションを交えながらわかりやすく解説します。
中間解析と多重検定の問題
臨床試験では、最終解析で有意水準 \(\alpha =0.05\) を設定するのが一般的です。
しかし、例えば 2回の中間解析+最終解析 を行う場合、単純に各解析で \(\alpha =0.05\) を使うと、全体の第一種過誤率は大幅に増加します。
数学的には、
\[\alpha _{\mathrm{overall}}=1-(1-\alpha )^k\]
で近似され、k は解析回数です。
例えば k=3 の場合、
\[\alpha _{\mathrm{overall}}\approx 1-(0.95)^3=0.14\]
となり、FWERが14%に跳ね上がります。これでは科学的妥当性が失われます。
α消費関数法の基本概念
α消費関数法は、試験全体での有意水準(例えば \(\alpha =0.05)\)を「時間軸に沿って少しずつ消費」する考え方です。
定義
試験の情報量(information fraction)を \(t\in [0,1]\) とします。
- t=0:試験開始
- t=1:最終解析
α消費関数を \(\alpha (t)\) とすると、
- \(\alpha (0)=0\)
- \(\alpha (1)=\alpha _{\mathrm{total}}\)
を満たす関数を設計します。
各中間解析時点 \(t_i\) において、累積で消費できる有意水準は \(\alpha (t_i)\) です。
- \(0 \leq t \leq 1\)のtに対して定義されます。
- α消費関数はtの単調増加関数
- \(\alpha (0)=0\)、\(\alpha (1)=\alpha _{\mathrm{total}}\)
代表的なα消費関数
Pocock型
- 各解析でほぼ同じ有意水準を割り当てる。
- 早期解析でも比較的緩やかに有意判定が可能。
数式:
\[\alpha (t)=\alpha \cdot \log (1+(e-1)t)\]
O’Brien-Fleming型
- 初期解析では非常に厳しく、終盤で緩やかになる。
- 早期に誤判定しにくい。
数式:
\[\alpha (t)=2\left( 1-\Phi \left( \frac{z_{\alpha /2}}{\sqrt{t}}\right) \right)\]
ここで \(\Phi\) は標準正規分布の累積分布関数。
Hwang-Shih-DeCani型
- パラメータ \(\gamma\) により柔軟に調整可能。
- \(\gamma \rightarrow 0\) でO’Brien-Fleming型に近似。
数式:
\[\alpha (t)=\alpha \cdot \frac{1-e^{-\gamma t}}{1-e^{-\gamma }}\]
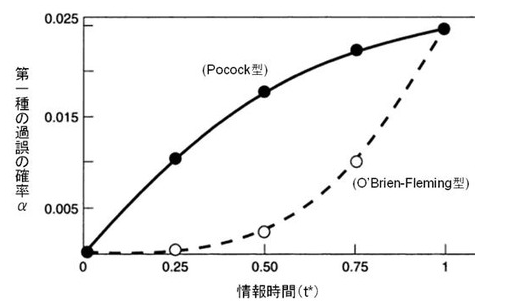
https://statmedoo.publog.jp/archives/6427505.html
- Pocock型は均等に消費。
- O’Brien-Fleming型は初期にほぼゼロ、終盤で一気に消費。
具体例
総α = 0.05、情報量比 t=0.33,0.67,1.0 の場合を考えます。
Pocock型
- 各解析でおよそ \(\alpha \approx 0.0167\) を割り当て。
- 判定基準は一貫して緩やか。
O’Brien-Fleming型
- 1回目:\(\alpha \approx 0.0005\)
- 2回目:\(\alpha \approx 0.004\)
- 最終解析:\(\alpha \approx 0.045\)
- 初期は非常に厳しいが、最終解析でほぼ通常の水準に戻る。
Rによるシミュレーション例
library(gsDesign)
# 総α = 0.05, 3回解析
design_pocock <- gsDesign(k=3, alpha=0.05, test.type=2, sfu=”Pocock”)
design_obf <- gsDesign(k=3, alpha=0.05, test.type=2, sfu=”OF”)
print(design_pocock)
print(design_obf)
# グラフ描画
plot(design_pocock, main=”Pocock型 α消費関数”)
plot(design_obf, main=”O’Brien-Fleming型 α消費関数”)
このコードにより、各解析時点での境界値(critical value)が出力され、グラフで視覚的に確認できます。
ベイズ的アプローチとの比較
考え方の違い
- 第一種過誤率(Type I error)を試験全体で制御することを目的とする。
- 有意水準を時間軸に沿って分配することで、試験途中の解析を可能にする。
- 「境界値(critical value)」を設定し、超えたら試験を停止する。
- 事前分布(prior distribution)とデータから得られる尤度を組み合わせ、事後分布(posterior distribution)を更新する。
- 中間解析では「事後確率(posterior probability)」を基準に意思決定する。
- 例えば「治療効果が0より大きい確率が95%以上なら試験を停止」といったルールを設定できる。
数理的表現
頻度論的枠組みでは、
\[P(\mathrm{Reject\ }H_0\mid H_0\mathrm{\ true})\leq \alpha\]
を保証する。
ベイズ的枠組みでは、
\[P(\theta >0\mid \mathrm{Data})>p^*\]
という条件を満たすかどうかで判断する。ここで \(\theta\) は治療効果、\(p^*\) は閾値(例:0.95)。
実務的な違い
- 頻度論的アプローチは規制当局(FDA, PMDA)で標準的に受け入れられている。
- ベイズ的アプローチは柔軟性が高く、特に希少疾患や小規模試験で注目されている。
- ただし、規制当局の承認には「事前分布の妥当性」や「透明性」が強く求められる。

製薬企業のケーススタディ
ケース1:大規模第III相試験(抗がん剤)
ある製薬企業は、抗がん剤の第III相試験で O’Brien-Fleming型のα消費関数を採用。
- 中間解析は2回設定(情報量比 0.33, 0.67)。
- 1回目の解析では有意水準が非常に厳しく設定されていたため、早期終了には至らず。
- 最終解析で有意差が確認され、規制当局に提出。
- この設計により「早期に誤判定しない」という信頼性を確保できた。
ケース2:希少疾患試験(ベイズ的アプローチ)
別の企業は希少疾患治療薬の試験で ベイズ的中間解析を採用。
- 事前分布は「既存治療の効果+専門家の知見」を組み合わせて設定。
- 中間解析で「治療効果がプラセボより優れる確率が97%」と算出され、試験を早期終了。
- 規制当局への申請では「事前分布の根拠」「シミュレーションによる誤判定率の評価」を詳細に提出。
- 承認に至ったが、頻度論的アプローチよりも審査に時間を要した。
ケース3:ハイブリッド型
最近では、頻度論的α消費関数法+ベイズ的解析を組み合わせる試験も増えている。
- 頻度論的枠組みで第一種過誤率を制御しつつ、ベイズ的解析で「臨床的意義」を補足。
- これにより、規制当局の要件を満たしながら、医療現場にとって直感的な解釈を提供できる。
まとめ
中間解析におけるα消費関数法は、試験全体の第一種過誤率を制御しながら柔軟な意思決定を可能にする頻度論的手法です。Pocock型やO’Brien-Fleming型などの関数により、解析時点ごとの有意水準を調整できます。一方、ベイズ的アプローチは事後確率に基づく判断を可能にし、特に希少疾患や小規模試験で有用です。製薬企業では両手法を使い分け、信頼性と柔軟性を両立させる設計が進んでいます。規制対応と臨床的意義の両立が今後の鍵です。