中間解析における頻度論とベイズ流アプローチ― 2000年までの理論的展開を振り返る
記事の目次
Toggleはじめに
臨床試験において「中間解析(interim analysis)」は、試験途中で蓄積されたデータを解析し、試験の継続か中止かを判断する重要な仕組みです。倫理的な観点からも、効果が明らかに優れている治療を早期に患者へ届けたり、逆に有害事象が強い治療を早期に中止することは不可欠です。統計学的にも、中間解析は試験デザインや推測方法に大きな影響を与えるため、1970年代以降盛んに研究されてきました。
2000年に発表された2つの総説論文――松井・宇野・小山による「頻度論的アプローチ」、宇野・松井・小山による「ベイズ流アプローチ」――は、それぞれの立場から中間解析の方法論を整理したものです。本記事では、この2つの論文を踏まえ、当時までにどのような理論的展開が行われてきたのかを振り返り、頻度論とベイズ流の違いをわかりやすく解説します。
中間解析については下記記事で解説しているので、興味がある方は是非ご一読ください。

頻度論的アプローチの展開
背景
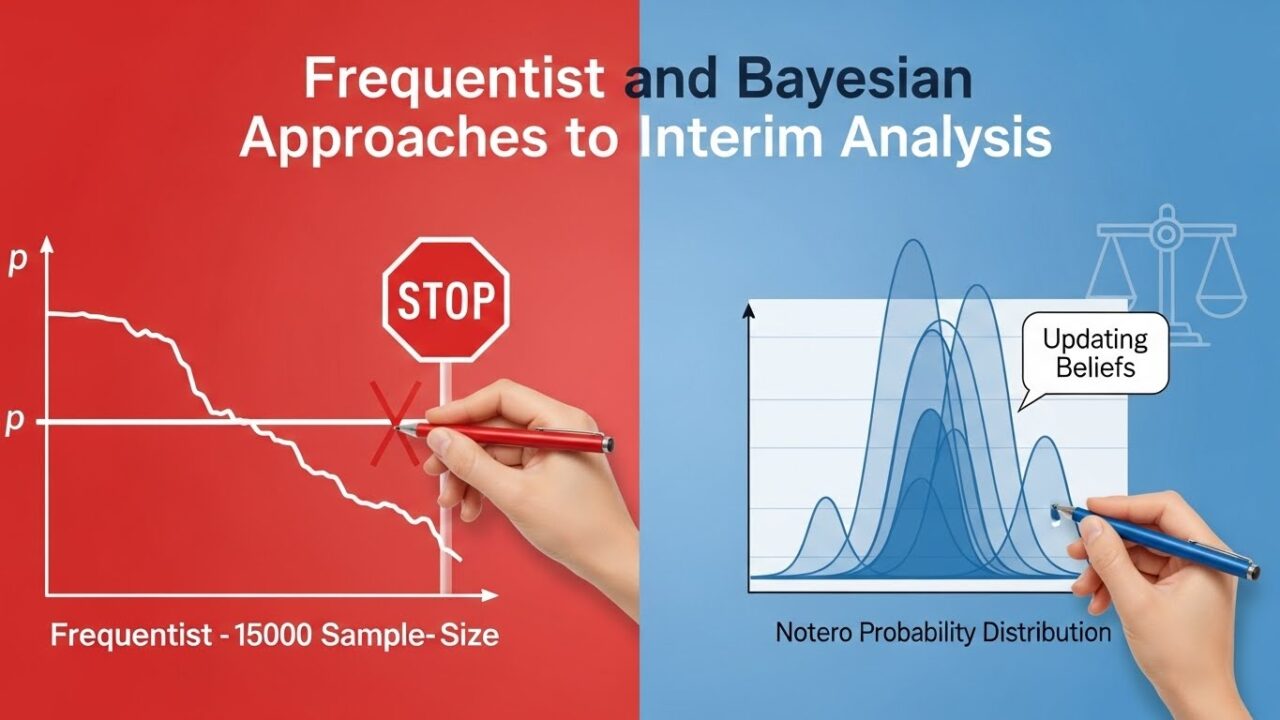
頻度論的アプローチは、仮説検定の枠組みに基づき「第一種の過誤(Type I error)」を制御することを中心に発展してきました。中間解析を繰り返すと、単純に有意水準を固定した検定を行うだけでは過誤率が累積し、試験全体の誤りが増大してしまいます。そのため、境界(boundary)を設定し、試験全体での誤り率を一定に保つ工夫が必要となります。
- 繰り返し検定アプローチ
Wald (1947) の逐次検定に端を発し、Pocock (1977) や O’Brien & Fleming (1979) が群逐次デザインを提案しました。これにより、一定数の症例が集まるごとに解析を行い、境界を超えた場合に試験を中止する仕組みが整いました。 - 境界アプローチ
Pocock型境界は「早期から比較的緩やかな基準」を設定し、O’Brien-Fleming型境界は「初期は厳しく、後期は緩やか」な基準を設定する特徴があります。これにより、試験全体の第一種過誤を制御しつつ、早期中止の可能性を調整できます。 - α消費関数(Lan & DeMets 法)
1980年代以降、解析回数や時点が事前に固定できない現実的な試験に対応するため、柔軟な方法が開発されました。Lan & DeMets (1983) による「α消費関数」は、情報量の進捗に応じて第一種過誤を“消費”する考え方であり、臨床試験の複雑な実情に即した方法として広く用いられるようになりました。 - 確率打ち切り法(Stochastic Curtailment)
条件付き検出力に基づき「このまま試験を続けた場合に有意差が得られる確率」を評価し、一定の閾値を下回れば中止するという方法です。これは後にベイズ流の予測確率アプローチと密接に関連する概念です。
頻度論的アプローチは「過誤率の制御」を明確に保証する点で信頼性が高く、検証的試験(第III相試験など)に適しています。しかし、解析回数や時点を事前に定める必要があること、複雑な試験状況(多重評価項目、生存時間解析など)への適用に課題が残されていました。
ベイズ流アプローチの展開
背景
ベイズ流アプローチは「事前分布と事後分布」に基づき、逐次的にデータを更新しながら意思決定を行う枠組みです。頻度論と異なり「過去に何回解析したか」「将来何回解析するか」といった要素は推測に影響しません。そのため、中間解析の枠組みに自然に適合し、柔軟な応用が可能です。
1980年代後半から、Berry (1989) や Korn et al. (1993) により安全性モニタリングや探索的試験での応用が進み、1990年代には検証的試験への適用可能性も議論されるようになりました。
- 事後分布に基づく方法
治療効果の事後分布から「被験薬が優れる確率」「劣る確率」を評価し、一定の閾値を超えた場合に試験を中止します。ベイズ流信頼区間(credibility interval)を用いる方法もあり、柔軟な設定が可能です。 - ベイズ流仮説検定
帰無仮説と対立仮説に事前分布を設定し、事後オッズ比に基づいて中止規準を構成します。これはWaldのSPRT(Sequential Probability Ratio Test)と密接に関連しています。 - ベイズ流決定理論
損失関数を設定し、事後期待損失を最小化する行動を選択する方法です。試験の中止・継続を「損失の比較」として定式化でき、理論的には最適な症例数の設計も可能です。ただし、損失関数の設定が主観的で複雑になるという課題があります。 - 予測確率に基づく方法
試験終了時の統計量が棄却域に入る確率を予測分布から求め、その確率に基づき中止規準を構成します。これは頻度論的な「条件付き検出力」と密接に関連しており、両者の橋渡し的な役割を果たします。
ベイズ流アプローチは「柔軟性」と「逐次的更新」という強みを持ち、探索的試験や安全性モニタリングに適しています。また、外部情報(他試験の結果など)を取り込むことも容易です。一方で、事前分布や損失関数の設定に主観が入りやすく、頻度論的な過誤率の保証がない点が課題とされました。
頻度論とベイズ流の比較
| 観点 | 頻度論的アプローチ | ベイズ流アプローチ |
| 基本枠組み | 仮説検定、過誤率制御 | 事前分布と事後分布の更新 |
| 中止規準 | 境界設定(Pocock, OBF, α消費関数など) | 事後分布、事後オッズ、損失関数、予測確率 |
| 強み | 過誤率制御が明確、検証的試験に適合 | 柔軟性、逐次的更新、外部情報の取り込み |
| 弱み | 解析回数・時点を事前に固定する必要 | 事前分布の主観性、過誤率保証がない |
| 主な応用 | 第III相試験など検証的試験 | 事前分布の主観性、過誤率保証がない |
2000年までの理論的展開を振り返って
2000年時点での総説論文は、頻度論とベイズ流それぞれのアプローチを整理し、臨床試験における中間解析の方法論がどのように発展してきたかを俯瞰するものでした。両者の違いを改めてまとめると以下のようになります。
- 頻度論的アプローチ:第一種過誤の制御を中心に据え、検証的試験での信頼性を重視してきました。境界設定法(Pocock型、O’Brien-Fleming型)、α消費関数、確率打ち切り法などが開発され、試験全体の誤り率を一定に保ちながら柔軟に中止規準を構成することが可能になりました。特にLan & DeMets法は、解析回数や時点が事前に固定できない現実的な試験に対応できる点で大きな進展でした。
- ベイズ流アプローチ:事前分布と事後分布の更新に基づき、逐次的に意思決定を行う柔軟な枠組みを提供しました。事後分布に基づく方法、ベイズ流仮説検定、決定理論、予測確率など多様なアプローチが提案され、探索的試験や安全性モニタリングに適用されました。外部情報を取り込める点や、逐次的な更新が自然に行える点は大きな強みでしたが、事前分布や損失関数の設定に主観が入りやすいこと、頻度論的な過誤率保証がないことが課題とされました。
両者の補完関係
興味深いのは、頻度論とベイズ流が必ずしも対立するものではなく、むしろ補完的に位置づけられる点です。例えば、頻度論的な「条件付き検出力」に基づく確率打ち切り法は、ベイズ流の「予測確率」と密接に関連しており、両者の考え方が橋渡しされる場面が見られます。また、頻度論的な境界設定法は過誤率の保証を提供し、ベイズ流の柔軟な意思決定枠組みは探索的試験や安全性評価に適しているため、試験の目的や状況に応じて両者を使い分けることが合理的です。
その後の展開への布石
2000年当時の総説は「最近の理論的展開」と題されていましたが、今日から振り返ると「当時までにどのような理論が積み重ねられてきたか」を整理したものと位置づけられます。その後20年以上の間に、臨床試験の環境はさらに複雑化し、アダプティブデザインやリアルワールドデータの活用など新しい潮流が生まれました。ベイズ流アプローチはその柔軟性からアダプティブデザインに自然に組み込まれ、頻度論的アプローチもα消費関数の拡張や多重評価項目への対応などが進みました。
つまり、2000年までの理論的展開は、今日の臨床試験デザインの基盤を築いた重要なステップであり、頻度論とベイズ流の両者を理解することは今なお不可欠です。
まとめ
臨床試験における中間解析は、試験途中で得られたデータを基に継続か中止かを判断する重要な仕組みです。2000年までの理論的展開を振り返ると、頻度論的アプローチは第一種過誤の制御を中心に、群逐次デザインや境界設定法、α消費関数などを発展させ、検証的試験での信頼性を確保してきました。一方、ベイズ流アプローチは事前分布と事後分布の更新に基づき、柔軟に意思決定を行う枠組みを提供し、探索的試験や安全性モニタリングに適用されました。両者は対立するものではなく、頻度論は過誤率の保証を、ベイズ流は柔軟性と外部情報の取り込みを強みとし、補完的に活用されてきました。これらの理論的展開は、その後のアダプティブデザインや複雑な試験環境への対応に大きな布石となったのです。
参考
中間解析における頻度論的アプローチ:最近の理論的展開 (2000, 松井 茂之, 宇野 一, 小山 暢之)
https://www.jstage.jst.go.jp/article/jjb/21/Special_Issue/21_Special_Issue_S87/_article/-char/ja
中間解析におけるベイズ流アプローチ:最近の理論的展開(2000, 宇野 一, 松井 茂之, 小山 暢之)
https://www.jstage.jst.go.jp/article/jjb/21/Special_Issue/21_Special_Issue_S125/_article/-char/ja