はじめに
臨床試験の統計的評価といえば、長らく頻度論（frequentist）に基づく仮説検定が主流でした。しかし近年、探索的試験や Proof-of-Concept（POC）試験において ベイズ流アプローチが注目されています。特に、患者数が限られる難治性疾患領域では「小さいサンプルでも意思決定が可能」「途中で柔軟に試験を止められる」などの利点が大きいのです。
本記事では、二値エンドポイント（成功/失敗）を持つ単群臨床試験におけるベイズ流デザインの基本を、数式と図解を交えて解説します。
ベイズ流枠組みの基本
臨床試験で「成功確率」を推定する場合、ベイズ流では ベータ分布を事前分布として設定します。
成功確率 \(\pi\) に対する事前分布を Beta(a,b) とすると、その確率密度関数は次の式で表されます。
\[f(x;a,b)=\frac{x^{a-1}(1-x)^{b-1}}{B(a,b)},\quad 0\]
ここで、ベータ関数 B(a,b) は
\[B(a,b)=\int _0^1t^{a-1}(1-t)^{b-1}dt\]
です。平均と分散は以下の通り。
\[E[X]=\frac{a}{a+b},\quad Var[X]=\frac{ab}{(a+b)^2(a+b+1)}\]
ベイズ更新
試験で n 人中 s 人が成功した場合、事後分布は次のように更新されます。
\[\pi |data\sim Beta(a+s,b+n-s)\]
この「自然共役事前分布」の性質により、積分計算なしで簡単に事後分布が得られるのが大きな利点です。
予測分布
さらに、将来の m 人に対して成功数 k が得られる確率は ベータ二項分布に従います。
\[Pr(K=k|s,n,m)={m \choose k}\cdot \frac{B(a+s+k,b+n-s+m-k)}{B(a+s,b+n-s)}\]
これにより「次に患者を追加したら成功数がどのくらい増えるか」を予測でき、中止規則の設計に役立ちます。
事前分布の選び方
事前分布 Beta(a,b) のパラメータは以下の方法で決定します。
- 過去試験データを利用：成功数を a、失敗数を b とする。ただし情報量を割り引くこともある。
- 専門家の意見を反映：成功確率の平均 M、分散 V から次式で導出。
\[a=\frac{M[M(1-M)-V]}{V},\quad b=\frac{(1-M)[M(1-M)-V]}{V}\]
情報がない場合：一様分布 Beta(1,1) を採用。
標本サイズの決定
ベイズ流では「十分な情報が得られた時点で終了」するのが本来の考え方ですが、実務上は最大標本サイズ N を決める必要があります。
方法1：精度に基づく方法
事後分布の信用区間幅が所定の精度を満たすように N を決定します。
\[Pr(L<\pi < U | data) > \omega\]
ここで、\(L=p^*-\delta /2、U=p^*+\delta /2\)
\(\omega\) は被覆確率（例：0.9）、\(\delta\) は区間幅（例：0.2）
方法2：事後分布に基づく方法
成功確率が対照値 \(p_0\) を超える確率が十分大きければ「有効」、目標値 \(p^*\) を超えない確率が大きければ「無効」と判断できるように N を決定します。
\[Pr(\pi >p_0|data)>\eta ,\quad Pr(\pi < p^*|data) > \zeta\]
中止規則（Stopping Rules）
ベイズ流では試験途中で柔軟に中止判断が可能です。代表的な方法は以下の通り。
- 事後分布に基づく有効中止
\[Pr(\pi >p^*|data)>T_S\] - 事後分布に基づく無効中止
\[Pr(\pi < p_0|data)>T_F\] - 予測分布に基づく有効中止
追加患者を含めた累積成功数が棄却値を超える確率が大きい場合。 - 予測分布に基づく無効中止
累積成功数が棄却値未満となる確率が大きい場合。
図解イメージ
例えば事前分布がBeta(1,1)としたときに、データとして患者10人中6人成功が得られたとします。このとき、事後分布は Beta(7,5)となり、下記のようにグラフが更新されます。
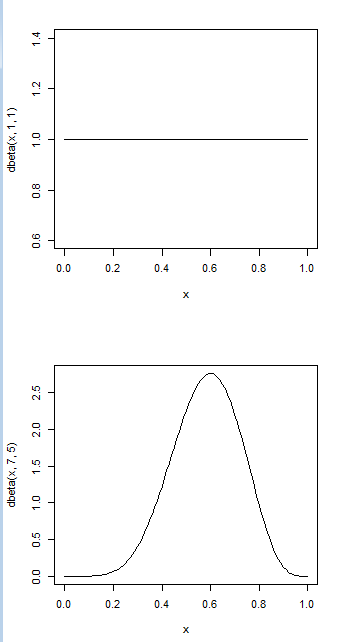
グラフで見ると、分布のピークが成功確率0.6付近に移動していることがわかります。
また中止境界は以下のようなものです。
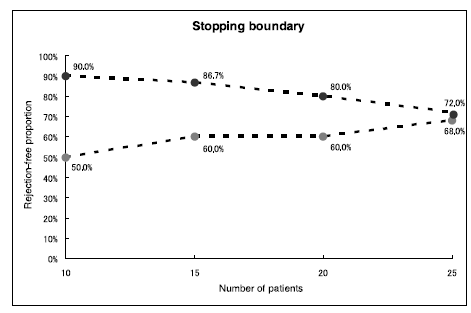
横軸：患者数、縦軸：成功割合。
境界線を超えれば「有効中止」、下回れば「無効中止」と判断します。
具体例(生体肝移植試験)
京都大学で行われた臨床試験を例にすると、主要エンドポイントは「移植後6か月以内の拒絶反応の有無」。
- 事前分布：情報がなかったため Beta(1,1)。
- 対照値 \(p_0\)：過去データより 0.55。
- 目標値 \(p^*\)：研究者の判断で 0.75。
- 最大標本サイズ：事後分布に基づく方法で \(N=25\)、棄却値 \(u_N=18\)。
- 中止規則：10例から5例ごとに中間解析。予測分布に基づき有効/無効中止を設定。
シミュレーションの結果、期待標本サイズは 14.4〜17.7 と、最大25例よりも少なく済むことが示されました。
実践的指針
感度分析：事前分布や閾値の設定が結果に与える影響を確認する。
シンプルな方法を優先：複雑な決定理論よりも、基本的なベータ分布更新と予測分布を活用。
中間モニタリングは柔軟に：患者リスクを最小化するため、早期中止の可能性を常に考慮。
まとめ
本記事では、探索的な単群臨床試験においてベイズ流デザインが持つ柔軟性と実用性について解説しました。特に、二値エンドポイント（成功／失敗）を対象とした試験において、ベイズ統計の基本的な枠組み、事前分布の選び方、標本サイズの決定方法、中止規則の設計、そして実例に基づく応用までを体系的に紹介しました。
ベイズ流アプローチの最大の利点は、試験途中で得られた情報を逐次的に反映しながら、意思決定を行える点にあります。これにより、患者数が限られる状況でも、事前情報を活用して効率的かつ倫理的な試験運営が可能になります。
ベイズ流デザインを導入する際の留意点として、事前分布や閾値の選択に対する感度分析の重要性、動作特性のシミュレーションによる検証、そして簡便な手法の選択が普及の鍵であることを強調しました。
ベイズ流デザインは、探索的試験や希少疾患領域における臨床研究において、今後ますます重要な役割を果たすと期待されます。
参考
二値エンドポイントの単群臨床試験におけるベイズ流デザイン（2008, 手良向 聡）
https://www.jstage.jst.go.jp/article/jjb/29/2/29_2_111/_article/-char/ja
