分布を選べるようになる:正規分布以外の世界を覗く―医薬統計の実務で“本当に使える”分布の考え方―
記事の目次
Toggleはじめに
統計の世界では「とりあえず正規分布」という文化が根強くあります。しかし、実務のデータは必ずしも正規分布に従いません。むしろ、正規分布“以外”の分布を適切に選べることこそ、統計家としての力量が問われるポイントです。
この記事では、医薬統計の現場でよく登場する二項分布、ポアソン分布、ガンマ分布を中心に、「どんなデータに、どの分布を使えばよいのか」を実務目線で整理します。
さらに、正規性がないときにどう対処するかという“現場で困らない”ための視点もまとめます。
正規分布だけでは世界を説明できない
正規分布は確かに便利です。中心極限定理のおかげで、平均値の分布はサンプルサイズが大きければ正規分布に近づきます。しかし、医薬統計の現場では次のようなデータが頻繁に登場します。
- 成功/失敗の2値データ(例:治療反応あり/なし)
- イベント回数(例:発作回数、入院回数)
- 時間データ(例:生存時間、治癒までの時間)
- 右に長い分布(例:薬物濃度、費用データ)
これらは正規分布では表現しにくく、別の分布を選ぶ必要があります。
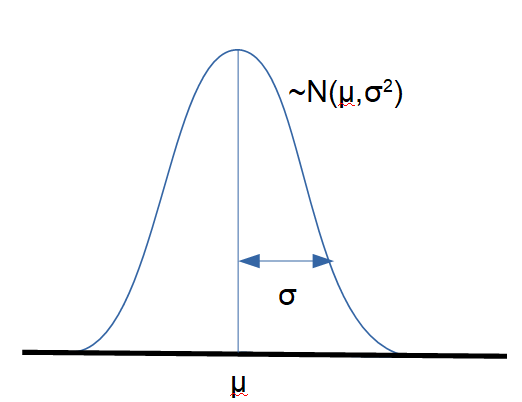
確率変数Xが、平均\(\mu\)、分散\(\sigma^2\)の正規分布に従うとき、確率密度関数は次の式で表されます。
\[f(x) = – \frac{1}{\sqrt{2 \pi \sigma^2}}exp \left[- \frac{(x – \mu)^2}{2\sigma^2} \right]\]
二項分布:成功・失敗の世界を扱う
使いどころ
- 治療反応の有無
- 副作用発現の有無
- 試験成功/失敗
- ある期間内に「成功」が起きる確率
試行回数を n、成功確率を p とすると、成功回数 X は
\[X\sim \mathrm{Binomial}(n,p)\]
確率質量関数は
\[P(X=k)={n \choose k}p^k(1-p)^{n-k}\]
期待値:\(E(X) = np\) , 分散:\(V(X) = np(1-p)\)
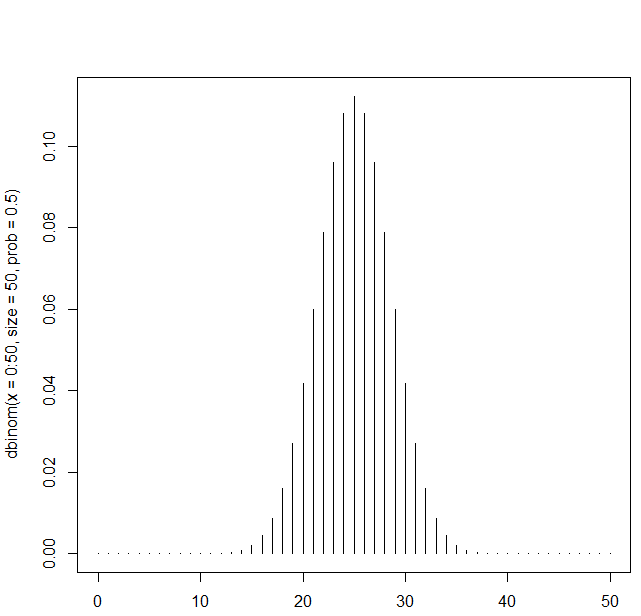
例:n=50, p=0.5の時の二項分布の概形
医薬統計での典型例
- 治療反応率の比較(例:A群 40%、B群 55%)
- 副作用発現率の推定
- ワクチン有効率の推定
実務のポイント
ポアソン分布:イベント回数を扱う
使いどころ
- 製造工程の欠陥数
- 発作回数
- 入院回数
- 有害事象の発生回数
平均発生率を \(\lambda\) とすると、回数 X は
\[X\sim \mathrm{Poisson}(\lambda )\]
確率質量関数は
\[P(X=k)=\frac{\lambda ^ke^{-\lambda }}{k!}\]
期待値:\(E(X) = \lambda\) , 分散:\(V(X) = \lambda\)
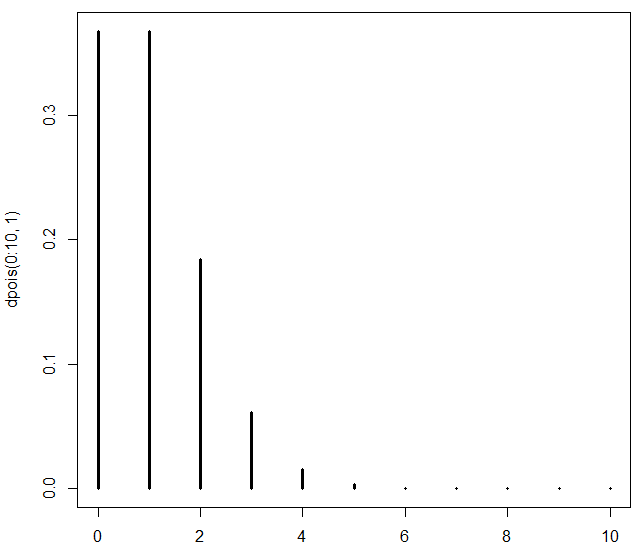
例:\(\lambda = 1\), \(0 \leq X \leq 10\)の時のポアソン分布の概形
医薬統計での典型例
- 喘息発作回数の比較
- 入院回数のモデル化
- 有害事象の発生率(例:AE/患者年)
■ 実務のポイント
- 平均 = 分散 が前提
- 実データでは分散が大きいことが多く、過分散が問題になる
- 過分散がある場合は
- 負の二項分布
- ポアソン回帰 + 乱効果を検討する
ガンマ分布:右に長い連続データを扱う
使いどころ
- 時間データ(治癒までの時間、待ち時間)
- 費用データ(医療費)
- 薬物濃度(右に長い分布になりやすい)
形状パラメータ k、尺度パラメータ \(\theta\) のとき
\[X\sim \mathrm{Gamma}(k,\theta )\]
確率密度関数は
\[f(x)=\frac{1}{\Gamma (k)\theta ^k}x^{k-1}e^{-x/\theta }\]
期待値:\(E(X) = k \theta\) , 分散:\(V(X) = k \theta^2\)
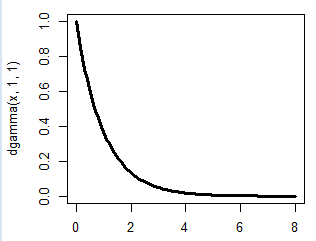
例:\(k= 1 , \theta = 1\)の時のガンマ分布の概形
医薬統計での典型例
- 医療費の分析(右に長い)
- 薬物濃度のモデル化
- 生存時間解析の基礎分布(指数分布はガンマ分布の特例)
実務のポイント
- GLM の ガンマ回帰 は費用データでよく使う
- ログリンクを使うと解釈がしやすい
- 外れ値に敏感なので、ロバスト推定も検討
医薬統計でよく出るその他の分布
医薬統計では、上記以外にも多様な分布が登場します。
■ 正規分布(Normal)
- 連続データの基本
- 血圧、体重、身長など
■ t 分布
- サンプルサイズが小さいときの平均比較
■ カイ二乗分布
- 分散分析
- 適合度検定
■ 指数分布・ワイブル分布
- 生存時間解析の基本
- ハザードの形状を柔軟に表現できる
■ 負の二項分布
- 過分散のあるカウントデータ
■ ベータ分布
- ベイズ推定で頻出
- 確率(0〜1)の分布
正規性がないとき、どうするか(実務的視点)
ここが最も重要なポイントです。
「正規性がない → 困った」ではなく、「正規性がない → ではどの分布が適切か?」
という発想が必要です。
分布を“当てにいく”アプローチ
- ヒストグラム
- QQプロット
- 箱ひげ図
分布の候補を考える
- 2値 → 二項
- カウント → ポアソン or 負の二項
- 時間 → 指数・ワイブル・ガンマ
- 右に長い → ガンマ・対数正規
- 二項 → ロジスティック回帰
- ポアソン → ポアソン回帰
- ガンマ → ガンマ回帰
分布にこだわらないアプローチ
- Wilcoxon 検定
- Mann–Whitney U 検定
- Kruskal–Wallis 検定
分布の仮定が弱く、実務で非常に使いやすい。
ブートストラップ
- 分布を仮定せず、データから再標本化して推定
- 信頼区間の推定に強力
- 医療費や濃度データで有効
- 外れ値に強い推定量
まとめ
医薬統計の実務では、データが常に正規分布に従うとは限りません。むしろ、成功・失敗の2値データ、イベント回数、右に長い時間データなど、正規分布では扱いにくいケースが日常的に現れます。こうした場面で、二項分布・ポアソン分布・ガンマ分布といった“正規分布以外の分布”を適切に選べることは、統計家としての重要なスキルです。
二項分布は治療反応や副作用発現などの2値データに、ポアソン分布は発作回数や入院回数などのカウントデータに、ガンマ分布は医療費や薬物濃度など右に長い連続データに適しています。これらの分布を理解し、GLM などのモデルで適切に扱うことで、データの本質をより正確に捉えることができます。
また、データがどの分布にもきれいに当てはまらない場合には、ノンパラメトリック手法やブートストラップ、ロバスト推定といった“分布に依存しない”アプローチも有効です。正規性がないからといって解析が行き詰まるわけではなく、むしろ選択肢が広がると捉えるべきでしょう。
分布を選べるようになることは、統計解析を「決まりきった手順」から「データの特徴を読み解く作業」へと進化させます。正規分布以外の世界を理解することで、医薬統計の解析力は大きく向上し、より信頼性の高い結論を導くことができるようになります。