回帰分析と相関:因果を見抜くために― 製薬データ解析の基礎から実務応用まで ―
記事の目次
Toggleはじめに
統計解析の世界で最も誤解されやすい概念のひとつが「相関」と「因果」です。特に製薬業界では、副作用の発生要因や治療効果の違いを理解するために、これらの区別が極めて重要になります。
本記事では、相関と因果の違い、単回帰・重回帰の基礎、製薬業界での応用例、そしてExcel と R での回帰分析のやり方を、図解や数式を交えながらわかりやすく解説します。
相関と因果の違いをわかりやすく解説
相関とは「2つの変数がどの程度一緒に変動するか」を示す指標です。
代表的なのが 相関係数(Pearson の r) で、
\[-1\leq r\leq 1\]
の範囲を取ります。
- r=0:相関なし
- r=1:完全な正の相関
- r=-1:完全な負の相関
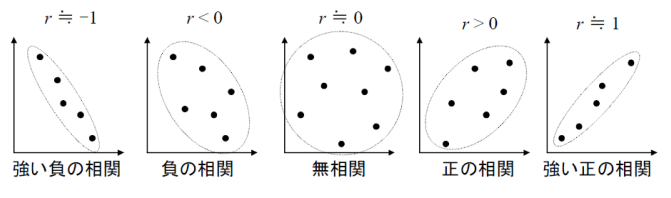
因果とは「A が変わると B が変わる」という原因と結果の関係 です。
相関と因果の違い
| 具体例 | 相関 | 因果 |
| アイスの売上と熱中症患者数 | 〇(夏に増える) | ✕(アイスが原因ではない) |
| 喫煙本数と肺がんリスク | 〇 | 〇(因果関係がある) |
なぜ相関だけでは因果を言えないのか?
理由は「交絡因子(confounder)」の存在です。
例:
- アイスの売上
- 熱中症患者数
- 気温(交絡因子)
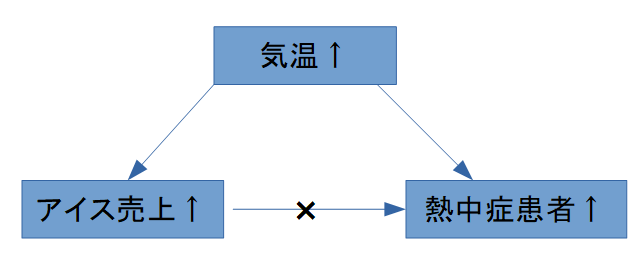
このように、第三の要因が両方に影響している場合、相関はあっても因果ではありません。

単回帰・重回帰の基礎
単回帰分析とは?
1つの説明変数(X)で目的変数(Y)を説明するモデルです。
\[Y=\beta _0+\beta _1X+\varepsilon\]
- \(\varepsilon\) :誤差
- \(\beta _0\):切片
- \beta _1:傾き(X が 1 増えると Y がどれだけ変化するか)
重回帰分析とは?
複数の説明変数で Y を説明するモデルです。
\[Y=\beta _0+\beta _1X_1+\beta _2X_2+\cdots +\beta _pX_p+\varepsilon\]
例:
副作用発生(Y)を
- 年齢(X1)
- 体重(X2)
- 投与量(X3)
で説明する、など。
- 交絡因子を調整できる
- 因果に近づく推論が可能
- 実務データに適用しやすい
製薬業界での応用:副作用と患者属性の関係分析
製薬データでは、患者背景が複雑に絡み合うため、重回帰分析が非常に役立ちます。
ケース:副作用(例:肝機能異常)の発生要因を探る
● 目的変数
- 肝機能値(ALT)
● 説明変数
- 年齢
- BMI
- 投与量
- 併用薬の有無
- 性別
● モデル例
\[ALT=\beta _0+\beta _1(\mathrm{年齢})+\beta _2(\mathrm{BMI})+\beta _3(\mathrm{投与量})+\beta _4(\mathrm{併用薬})+\varepsilon\]
● 解析でわかること
- 併用薬が影響しているか
- 投与量が増えるとALT が上昇するか
- 高齢者でALT が上がりやすいか
Excel でできる回帰分析
Excel は初心者に最も使いやすいツールです。
手順
- データ分析ツールを有効化
- [ファイル] → [オプション] → [アドイン] → [分析ツール] を有効化
- データ分析 → 回帰分析 を選択
- 目的変数(Y)と説明変数(X)を指定
- 結果が自動で出力される
Excel 出力で見るべきポイント
- 係数(Coefficient):影響の大きさ
- p 値:統計的に有意か
- R²:モデルの説明力
10分程で回帰分析ができます。
R言語でできる回帰分析(コード付き)
R は製薬業界で最も使われる統計解析言語のひとつです。
単回帰
model <- lm(ALT ~ Dose, data = df)
summary(model)
重回帰
model <- lm(ALT ~ Age + BMI + Dose + ComboDrug, data = df)
summary(model)
結果の読み方
- Estimate:係数
- Pr(>t):p 値
- Adjusted R-squared:説明力
R は再現性が高く、規制当局(FDA/PMDA)でも推奨される解析環境として広く使われています。
因果を見抜くために:回帰分析の限界と注意点
回帰分析は強力ですが、万能ではありません。
- 観察データでは因果を断定できない
- 未測定の交絡因子が残る可能性
- モデルの仮定(線形性、独立性、正規性)が必要
- 副作用解析では「交絡因子の調整」が必須
- 年齢・性別・併用薬などを必ずモデルに入れる
- 因果推論が必要な場合は、傾向スコア・IPTW・マッチングなどの手法も検討する
まとめ
回帰分析は、データの背後にある構造を理解し、どの要因が結果に影響しているのかを定量的に捉えるための最も基本的で強力な手法です。相関はあくまで「一緒に変動している」という関係を示すに過ぎず、因果関係を直接証明するものではありませんが、回帰分析を用いることで、交絡因子を調整しながら各要因の影響をより正確に評価することができます。特に製薬業界では、副作用の発生要因や治療効果の違いを理解するために、患者属性や投与量、併用薬など複数の要因が複雑に絡み合うため、重回帰分析は欠かせないツールです。Excel で手軽に始めることもでき、R 言語を使えばより高度で再現性の高い解析が可能になります。回帰分析は因果推論の完全な答えではありませんが、因果を見抜くための第一歩として、そして製薬データ解析の基盤として、初学者から実務者まで必ず身につけておくべき重要な技術だと言えます。