因果推論の“識別”を数学的に理解する:do演算・操作変数・バックドア条件
因果推論では、「因果効果を推定する」以前に、そもそもその因果効果が識別(identification)可能かどうかを判断する必要があります。識別とは、観測データの分布から因果効果が一意に決まることを意味します。識別できなければ、どれだけデータが増えても因果効果は推定できません。
本記事では、Pearl の因果モデルを数学的に整理し、バックドア条件の直感的な証明、操作変数法の識別条件を線形代数で理解し、最後に実務での落とし穴をまとめます。
記事の目次
TogglePearl の因果モデルを数理的に整理する
Pearl の因果推論は、構造方程式モデル(Structural Causal Model; SCM)を基盤にしています。SCM は次の3つの要素から構成されます。
構造方程式
各変数 \(X_i\) は、親ノード \(\mathrm{pa}(X_i)\) と外生変数 \(U_i\) の関数として定義されます。
\[X_i=f_i(\mathrm{pa}(X_i),U_i)\]
ここで
- \(U_i\) は外生ノイズ(未観測要因)
- \(f_i\) は決定論的関数
です。
do 演算の定義
介入 do(X=x) は、構造方程式を強制的に書き換える操作です。
\[P(Y\mid do(X=x))=\sum _uP(Y\mid X=x,u)P(u)\]
これは「X を外生的に固定し、X の親ノードとの因果関係を切断する」ことを意味します。
因果効果の識別とは
観測分布 \(P(X,Y,Z,\dots )\) から
\[P(Y\mid do(X=x))\]
を一意に計算できるとき、因果効果は識別可能といいます。
識別できなければ、どれだけデータが増えても因果効果は推定できません。
バックドア条件の証明の直感
バックドア条件は、因果推論で最も重要な識別条件のひとつです。
バックドア条件とは
集合 Z が \(X\rightarrow Y\) の因果効果を識別するためのバックドア集合であるとは、
- Z が X のすべてのバックドアパスをブロックする
- Z は X の子孫を含まない
ことをいいます。

バックドア調整式
バックドア条件を満たす Z が存在するとき、
\[P(Y\mid do(X=x))=\sum _zP(Y\mid X=x,Z=z)P(Z=z)\]
が成り立ちます。
証明の直感
ポイントは次の2つです。
① do(X=x) によって X の親ノードが切断される
介入後の分布は
\[P(Y\mid do(X=x))=\sum _uP(Y\mid X=x,u)P(u)\]
ですが、交絡因子 Z が U の情報を十分に持っていれば、
\[P(Y\mid X=x,Z=z)=\sum _uP(Y\mid X=x,u)P(u\mid Z=z)\]
となります。
② Z を条件づけることで、観測データの世界で介入を模倣できる
観測データでは
\[P(Y\mid X=x,Z=z)\]
を直接計算できます。
さらに、介入後の Z の分布は観測分布と同じなので、
\[P(Z=z\mid do(X=x))=P(Z=z)\]
が成り立ちます。
これらを組み合わせると、
\[P(Y\mid do(X=x))=\sum _zP(Y\mid X=x,Z=z)P(Z=z)\]
が導かれます。
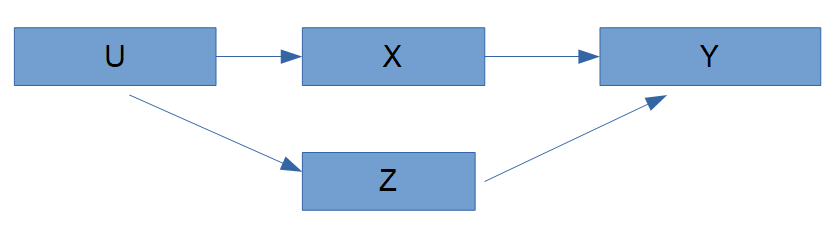
バックドア調整のイメージとして、Z を条件づけることで、U の影響を遮断し、X→Y の純粋な因果効果を取り出せます。
操作変数法(IV)の識別条件を線形代数で理解する
操作変数法(Instrumental Variables; IV)は、未測定交絡がある場合に因果効果を識別するための方法です。
基本モデル
線形モデルを考えます。
\[Y=\beta X+\epsilon\]
\[X=\pi Z+\eta\]
ここで
- Z:操作変数
- \(\epsilon\) :誤差項(未測定交絡を含む)
IV の識別条件は次の2つです。
IV の識別条件
① Relevance(関連性)
\[\mathrm{Cov}(Z,X)\neq 0\]
つまり、Z が X を動かす力を持つこと。
② Exogeneity(外生性)
\[\mathrm{Cov}(Z,\epsilon )=0\]
つまり、Z が Y に直接影響しないこと。
線形代数で理解する識別
観測可能な共分散行列を
\[\Sigma =\left( \begin{matrix}\mathrm{Var}(Z)&\mathrm{Cov}(Z,X)&\mathrm{Cov}(Z,Y)\\ \mathrm{Cov}(X,Z)&\mathrm{Var}(X)&\mathrm{Cov}(X,Y)\\ \mathrm{Cov}(Y,Z)&\mathrm{Cov}(Y,X)&\mathrm{Var}(Y)\end{matrix}\right)\]
とします。
IV 推定量は
\[\hat {\beta }_{IV}=\frac{\mathrm{Cov}(Z,Y)}{\mathrm{Cov}(Z,X)}\]
です。
識別可能であるとは、分母が 0 でないことに対応します。
つまり、
\[\mathrm{Cov}(Z,X)\neq 0\]
が識別条件です。
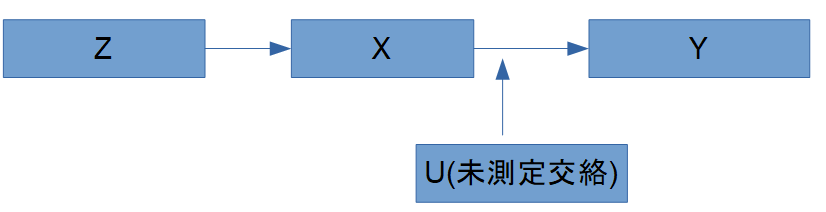
Z は U に影響されず、X を通じてのみ Y に影響します。
実務での因果推論の落とし穴
因果推論は理論的には美しいですが、実務では多くの落とし穴があります。
未測定交絡(Unmeasured Confounding)
バックドア条件を満たす Z が存在しない場合、因果効果は識別できません。
例:医療データ
- 健康意識 → 運動量 → 健康度
- 健康意識 → 食生活 → 健康度
健康意識が未測定なら、運動の効果は識別できません。
弱い操作変数(Weak IV)
\[\mathrm{Cov}(Z,X)\approx 0\]
の場合、IV 推定量は不安定になり、分散が爆発します。
実務では、F 統計量が 10 未満なら弱い IV とみなすことが多いです。
選択バイアス(Selection Bias)
介入や観測が特定のサブグループに偏ると、識別が破綻します。
モデルの誤指定
線形モデルを仮定しても、真の因果関係が非線形なら識別が崩れます。
まとめ
因果推論において最も重要なのは、因果効果が「推定できるかどうか」ではなく、そもそも「識別できるかどうか」です。識別とは、観測データの分布から因果効果が一意に決まることを意味し、この条件が満たされなければ、どれほどデータ量を増やしても正しい因果効果には到達できません。
Pearl の構造的因果モデル(SCM)は、因果関係を数学的に定義する強力な枠組みであり、do 演算によって介入後の分布を厳密に記述できます。バックドア条件は、交絡因子を適切に調整することで、観測データの世界で介入を模倣できることを保証する識別条件です。その背後には、介入によって切断される因果経路と、条件づけによって遮断される交絡経路の対応関係という明確な直感があります。
一方、未測定交絡が存在する場合にはバックドア調整が不可能となり、操作変数法(IV)が有力な代替手段になります。IV の識別条件は、線形代数的には「Z が X を十分に動かす(関連性)」ことと、「Z が誤差項と独立(外生性)」であることに対応し、共分散構造から因果効果を一意に解くための条件として理解できます。ただし、弱い IV の問題は実務で頻繁に発生し、推定量の分散が爆発するため注意が必要です。
実務の因果推論では、未測定交絡、弱い操作変数、選択バイアス、モデル誤指定など、識別を破壊する要因が数多く存在します。これらの問題は、データ量や高度な機械学習モデルでは解決できず、因果構造そのものを理解し、適切な識別条件を満たす設計や分析が不可欠です。
因果推論の本質は「識別」にあり、識別できて初めて推定が意味を持ちます。数学的な枠組みと直感的な理解を両立させることで、因果推論はより強力で信頼できる分析手法として活用できるようになります。