点推定値の基礎から学ぶ:推定量の性質とその意義

記事の目次
Toggleはじめに
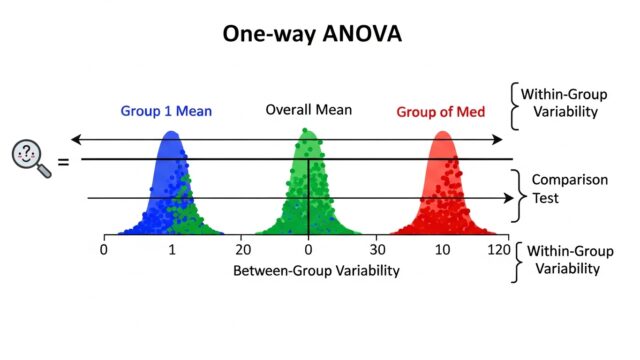
統計学において「推定」とは、母集団の未知のパラメータを標本データから推測することを指します。その中でも「点推定値」は、母数の値を一つの数値として推定する方法です。例えば、母平均 \(\mu\) を標本平均 \(\bar {X}\) で推定するのは典型的な点推定です。
本記事では、点推定の基礎から始め、推定量の重要な性質である 普遍推定量(不偏性)、有効推定量、漸近有効性、十分性、一致性 を体系的に解説します。数式や図解を交え、初心者から専門家まで理解しやすいように解説していきます。
点推定の基礎
母集団のパラメータ \(\theta\) を推定するために、標本データ \(X_1,X_2,\dots ,X_n\) を用います。推定量 \(\hat {\theta }\) は標本データの関数であり、確率変数です。
- 例:母平均の推定
\[\hat {\mu }=\bar {X}=\frac{1}{n}\sum _{i=1}^{n}X_i\] - 例:母分散の推定
\[\hat {\sigma }^2=\frac{1}{n}\sum _{i=1}^{n}(X_i-\bar {X})^2\]
推定量は「どのような性質を持つか」によって評価されます。以下でその代表的な性質を解説します。
不偏推定量(Unbiased Estimator)
推定量 \(\hat {\theta }\) の期待値が真の母数 \(\theta\) に一致するとき、不偏推定量と呼びます。
\[E[\hat {\theta }]=\theta\]
- 例:標本平均
\[E[\bar {X}]=\mu\]
よって \bar {X} は母平均の不偏推定量。 - 例:標本分散
\[\hat {\sigma }^2=\frac{1}{n}\sum _{i=1}^{n}(X_i-\bar {X})^2\]
は不偏ではなく、修正標本分散
\[S^2=\frac{1}{n-1}\sum _{i=1}^{n}(X_i-\bar {X})^2\]
が不偏推定量となります。
有効推定量(Efficient Estimator)
不偏推定量の中で、分散が最小のものを有効推定量といいます。
分散が0またはそれに近い不偏推定量を見つけていきたいが、実際は不可能です。
推定量の分散には理論的な下限があり、それを満たす推定量は「最良不偏推定量(MVUE)」と呼ばれます。このとき、クラメール・ラオ(Cramer-Rao)の不等式という定理を用います。
\[Var (\hat{\theta} \geq \frac{1}{I(\theta)})\]
ここで\(I(\theta)\)はフィッシャー情報量と呼び、
\[I(\theta) = E \left[\frac{\partial log(f(X|\theta))}{\partial \theta} \right]\]
以下ではクラメール・ラオの不等式について証明していきます。
今回は連続型の場合を考えていきます。
\(E(T)= \theta\)より、
\[\theta = \int_{- \infty}^{\infty} \dotsi \int_{- \infty}^{\infty} t(x_1 \cdots x_n) \prod_{i=1}^{n}f(x_i|\theta) dx_1 \cdots dx_n —(i)\]
\[1 =\int_{- \infty}^{\infty} \dotsi \int_{- \infty}^{\infty} \prod_{i=1}^{n}f(x_i|\theta) dx_1 \cdots dx_n —(ii) \]
(i),(ii)を両辺\(\theta\)で微分します。
\[1 = \int_{- \infty}^{\infty} \dotsi \int_{- \infty}^{\infty} t(x_1 \cdots x_n) \frac{\partial}{\partial \theta} \prod_{i=1}^{n}f(x_i|\theta) dx_1 \cdots dx_n —(iii)\]
\[0 =\int_{- \infty}^{\infty} \dotsi \int_{- \infty}^{\infty} \frac{\partial}{\partial \theta} \prod_{i=1}^{n}f(x_i|\theta) dx_1 \cdots dx_n —(iv) \]
(iii) – \(\theta \times \) (iv)を行い、
$$
\begin{eqnarray}
1 &=& \int \cdots \int (t(x_1, \ldots, x_n) – \theta)
\frac{\partial}{\partial \theta}
\prod_{i=1}^{n} f(x_i|\theta) \, dx_1 \cdots dx_n \\
&=& \int \cdots \int (t(x_1, \ldots, x_n) – \theta)
\frac{\partial}{\partial \theta}
\log \left( \prod_{i=1}^{n} f(x_i|\theta) \right)
\prod_{i=1}^{n} f(x_i|\theta) \, dx_1 \cdots dx_n \\
&=& E \left[ (T – \theta)
\frac{\partial}{\partial \theta}
\log \left( \prod_{i=1}^{n} f(X_i|\theta) \right) \right]
\quad \text{— (v)}
\end{eqnarray}
$$
\[\because \frac{\partial f(x|\theta)}{\partial \theta} = \frac{\partial log f(x|\theta)}{\partial \theta} f(x|\theta)\]
\(E \left[\frac{\partial}{\partial \theta}log(\prod_{i=1}^{n}f(X_i|\theta)) ^{2}\right] \)が存在するとして、(v)にコーシーシュワルツの不等式を適用します。
任意のtの実数に対して、
$$
\begin{eqnarray}
E[t(X-Y)^{2}] \geq 0 \\
\leftrightarrow t^{2}E(X^{2}) – 2tE(XY) + E(Y^2) \geq 0
\end{eqnarray}
$$
判別式を用いて、
$$
\begin{eqnarray}
\frac{D}{4} = (E(XY))^{2} – E(X^2)E(Y^2) \leq 0 \\
\leftrightarrow (E(XY))^{2} \leq E(X^2)E(Y^2)
\end{eqnarray}
$$
$$
\begin{eqnarray}
1 &=& \left[E(T – \theta)\frac{\partial}{\partial \theta}log (\prod_{i=1}^{n}f(x_i|\theta)) \right]^2\\
&\leq& E[(T- \theta)^2] E[(\frac{\partial}{\partial \theta}log (\prod_{i=1}^{n}f(x_i|\theta)))^2]
\end{eqnarray}
$$
ここで、
\[E[(T- \theta)^2] = V(T)\]
$$
\begin{eqnarray}
E[(\frac{\partial}{\partial \theta}log (\prod_{i=1}^{n}f(x_i|\theta)))^2] &=& E[(\sum_{i=1}^{n}\frac{\partial}{\partial \theta}log f(x_i|\theta))^2]\\
&=& \sum_{i=1}^{n}E[(\frac{\partial}{\partial \theta} log f(x_i|\theta))^2] + \sum_{i=1}^{n}\sum_{j=1}^{n}E \left[(\frac{\partial log f(x_i|\theta)}{\partial \theta})(\frac{\partial log f(x_j|\theta)}{\partial \theta})\right]\\
&=& n I(\theta)
\end{eqnarray}
$$
となることから、\(V(T) \geq \frac{1}{nI(\theta)}\)となる。 Q.E.D
漸近有効性(Asymptotic Efficiency)
標本サイズ\(n\)が大きくなるとき、推定量の分布が正規分布に近づき、その分散がクラメール・ラオの不等式に一致する場合、漸近有効性をもつといいます。
- 例:最尤推定量(MLE)
\[\tilde{\theta_{MLE}} ~ N\left(\theta, \frac{1}{nI(\theta)} \right)\] - 大標本では最尤推定量が漸近的に最良となります。
十分性(Suffiiency)
統計量\(T(X)\)が母数\(\theta\)に関して十分であるとは、標本データの情報をすべて保持していることを意味しています。
統計量\(T(X)\)が母数\(\theta\)が十分統計量であるとは、標本の分布が
\[f(x|\theta) = g(T(x),\theta) h(x)\]
と分解できます。
例:正規分布 平均\(\mu\)の推定において、標本平均\(\bar{X}\)は十分統計量。
一致性(Consistency)
推定量\(\tilde{\theta_n}\)が標本サイズ\(n \rightarrow \infty\)のとき、母数\(\theta\)に収束する性質を一致性といいます。
まとめ
点推定とは、母集団の未知のパラメータを標本データから一つの数値として推定する方法であり、統計学の基礎を成す重要な概念です。推定量にはいくつかの性質があり、それらを理解することで推定の信頼性や妥当性を評価できます。まず、不偏推定量は平均的に正しい推定を行う性質を持ち、有効推定量は不偏推定量の中で分散が最小となるものを指します。さらに、標本サイズが大きくなるときに理論的に最良の推定量となる漸近有効性も重要です。また、十分統計量は母数に関する情報を失わずにデータを要約できる統計量であり、一致性は標本サイズが増えるにつれて推定量が真の値に収束する性質を意味します。これらの性質は、推定量を選択・評価する際の基本的な基準であり、特に医薬品開発や規制科学の分野では、臨床試験の解釈や承認に直結するため不可欠です。総じて、点推定の理解は統計学の理論的基盤を支えると同時に、実務における意思決定の精度を高める役割を果たします。

![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/4aa03195.892069bb.4aa03196.39df6be9/?me_id=1213310&item_id=10288940&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F3200%2F32001435.jpg%3F_ex%3D300x300&s=300x300&t=picttext)