はじめに
生存時間解析は、医療・疫学・薬剤疫学・公衆衛生など幅広い分野で用いられる統計的手法です。典型的には「あるイベントが発生するまでの時間」を扱いますが、現実の臨床試験や疫学研究では、注目するイベント以外の要因によって観察が打ち切られることが少なくありません。これが「競合リスク (competing risks)」です。
例えば「心血管疾患による死亡」を解析したい場合でも、患者が「がんによる死亡」で先に亡くなれば、心血管疾患による死亡は観測できません。このように、あるイベントが発生すると他のイベントは観測できなくなる状況を「競合リスクイベント」と呼びます。
本記事では、競合リスクイベントの概念、解析上の課題、代表的な統計的手法を整理し、医療分野での応用をわかりやすく解説します。
生存時間解析については以下の記事で紹介しているので興味がある方は是非ご一読ください。
競合リスクイベントとは何か
- 競合リスクイベントとは、ある対象に複数のイベントが起こり得るが、一つのイベントが発生すると他のイベントは観測できなくなる状況を指します。
- 例
- 心血管疾患による死亡 vs 他原因による死亡
- 治療中止（有害事象による） vs 治療中止（その他の理由） vs 治療中止前の死亡
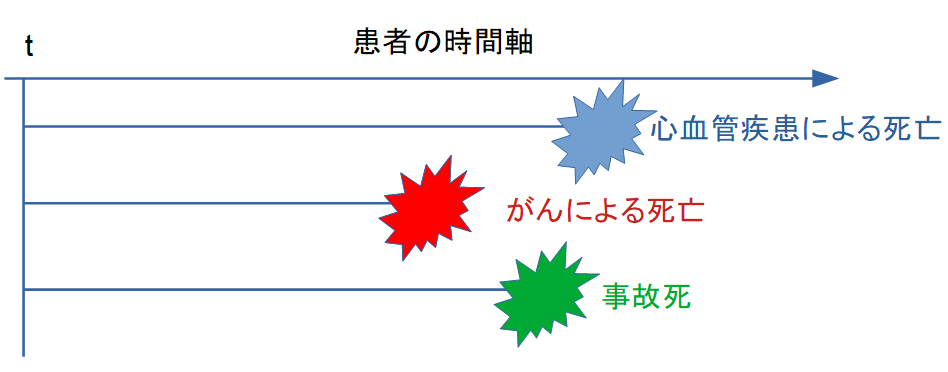
このように、イベント同士が「排他的」であるため、通常の生存時間解析（Kaplan-Meier推定など）をそのまま適用するとバイアスが生じることが知られています。
一般的な生存時間解析と競合リスクの問題
Kaplan-Meier推定量の限界
Kaplan-Meier推定量は「無情報センサー (non-informative censoring)」を仮定します。つまり、観察打ち切りがイベント発生確率に影響しないと仮定しています。
しかし競合リスクイベントは「情報を持つセンサー (informative censoring)」です。例えば「がんによる死亡」は「心血管疾患による死亡」の発生確率に影響を与えるため、単純に打ち切りとして扱うと過大評価や過小評価が起こります。
競合リスク解析の基本的枠組み
競合リスク解析では、以下の二つの指標が中心となります。
原因別ハザード (Cause-specific hazard)
ある原因 k によるイベントの瞬間的発生率を表します。
\[\lambda _k(t)=\lim _{\Delta t\rightarrow 0}\frac{P(t\leq T \leq t + \Delta, event = k | T \geq t)}{\Delta t}\]
これは「時間 t まで生存している人が、次の瞬間に原因 k によるイベントを起こす確率」を意味します。
累積発生率 (Cumulative incidence function, CIF)
原因 k によるイベントが時間 t までに発生する確率を表します。
\[F_k(t)=P(T\leq t,\mathrm{event}=k)=\int _0^tS(u)\lambda _k(u)\, du\]
ここで S(u) は「時間 u までイベントが発生せず生存している確率」です。
CIFは「実際に観測されるイベント発生確率」を表すため、臨床試験や疫学研究での解釈に適しています。
解析方法の代表例
原因別ハザードモデル (Cause-specific Cox model)
- Cox比例ハザードモデルを原因ごとに適用する方法。
- 各イベントタイプを「イベント」として扱い、他のイベントは打ち切りとして処理する。
- 共変量の影響を「瞬間的な発生率」に対して評価できる。
数式：
\[\lambda _k(t|Z)=\lambda _{0k}(t)\exp (\beta _k’Z)\]
Fine-Grayモデル (Subdistribution hazard model)
- CIFを直接モデル化する方法。
- 「ある原因による累積発生率」に対する共変量の影響を評価できる。
- 臨床試験で「特定のイベントの累積発生率」を比較する際に有用。
数式：
\[\tilde {\lambda }_k(t|Z)=\tilde {\lambda }_{0k}(t)\exp (\gamma _k’Z)\]
ここで \(\tilde {\lambda }_k(t)\) は「サブディストリビューションハザード」と呼ばれる。
実例で考える：心血管疾患試験
- 目的：心血管疾患による死亡率を比較
- 競合リスク：がんによる死亡、事故死
- 解析方法：
- Cause-specific Coxモデル → 「心血管疾患死亡の瞬間的リスク」を評価
- Fine-Grayモデル → 「心血管疾患死亡の累積発生率」を評価
両者の結果は異なる解釈を持ちます。前者は「病態のメカニズム理解」に、後者は「臨床的な予後予測」に適しています。
実務での注意点
- イベント定義の工夫:
「再発」 vs 「再発前死亡」など、イベントの定義次第で競合リスク構造が変わる。 - タイデータの処理:
測定誤差で同時発生が起こる場合は「jittering」などで調整。 - 解釈の違い:
Cause-specific hazard → 瞬間的リスク
Fine-Grayモデル → 累積発生率
まとめ
競合リスクイベントとは、ある対象に複数のイベントが起こり得るが、一つのイベントが発生すると他のイベントは観測できなくなる状況を指します。典型例として「心血管疾患による死亡」と「他の原因による死亡」があり、どちらかが起きればもう一方は観測できません。
通常の生存時間解析で用いられるKaplan-Meier推定量は「無情報センサー」を仮定しているため、競合リスクイベントを単純に打ち切りとして扱うとバイアスが生じます。そこで、競合リスク解析では以下の二つの指標が重要になります。
- 原因別ハザード (Cause-specific hazard)：ある原因による瞬間的なイベント発生率
- 累積発生率 (Cumulative incidence function, CIF)：ある原因によるイベントが時間までに発生する確率
解析方法としては、Cox比例ハザードモデルを原因ごとに適用する「原因別ハザードモデル」と、CIFを直接モデル化する「Fine-Grayモデル」が代表的です。前者は病態理解やメカニズムの解析に、後者は臨床的な予後予測に適しています。
まとめると、競合リスクイベントを正しく扱うためには「イベント定義の工夫」「タイデータの処理」「解析手法の選択」が重要です。Cause-specificモデルとFine-Grayモデルはそれぞれ異なる解釈を持つため、研究目的に応じて使い分けることが求められます。
