統計学の基礎：標本分布を理解しよう
はじめに
統計学を学び始めると、最初に出会う大きな壁のひとつが「標本分布」という概念です。
「母集団」「標本」「推定」といった言葉は耳にしたことがあっても、標本分布とは何かを直感的に理解するのは簡単ではありません。
この記事では、統計学をこれから学ぶ方に向けて、標本分布の基本をわかりやすく解説します。数式や図解を交えながら、標本平均や標本分散の性質を丁寧に説明していきます。
母集団と標本
まずは基本的な用語から整理しましょう。
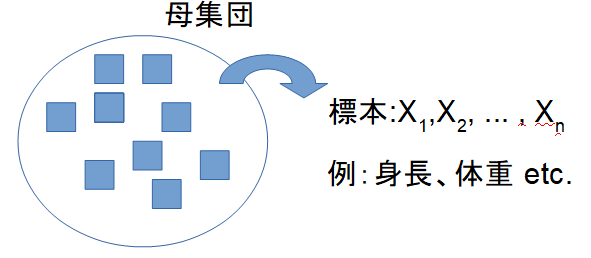
- 母集団 (population)
調べたい対象全体の集合。例：日本全国の高校生の身長。 - 標本 (sample)
母集団から抽出した一部のデータ。例：全国からランダムに選んだ100人の高校生の身長。
統計学では、母集団全体を調べることは難しいため、標本を使って母集団の性質を推定します。
標本平均と標本分散
標本から得られる代表的な統計量が「標本平均」と「標本分散」です。
標本平均:標本の平均値。
\[\bar{X} = \frac{1}{n}\sum_{i=1}^{n}X_{i}\]
ここで \(X_i\) は標本の各データ、\(n\) は標本サイズです。
標本平均の期待値、分散は以下のように導出できます。
$$
\begin{eqnarray}
E(\bar{X}) &=& E \left( \frac{1}{n}\sum_{i=1}^{n}X_{i} \right)\\
&=& \frac{1}{n} \left(E(X_1) + \cdots + E(X_n) \right) \\
&=& \mu
\end{eqnarray}
$$
$$
\begin{eqnarray}
V(\bar{X}) &=& V \left(\frac{1}{n}\sum_{i=1}^{n} \right)\\
&=& \frac{1}{n^{2}} V \left(\sum_{i=1}^{n} \right) \\
&=& \frac{1}{n^{2}} \left(V(X_1) + V(X_2) + \cdots + V(X_n) \right)\\
&=& \frac{\sigma^{2}}{n}
\end{eqnarray}
$$
これらより、
- 標本平均の期待値は母平均に一致します。
- 標本平均の分散は母分散をnで割ったものになります。つまり、nを十分大きくとれば、\(\bar{X}\)は\(\mu\)にほぼ一致します。これは「大数の法則」の直感的な背景です。
標本分散:標本のばらつきを表す指標。母分散の推定量として使われます。
\[S^{2}= \frac{1}{n-1}\sum_{i=1}^{n}(X_{i} – \bar{X})^{2}\]
※なぜ分母が n-1 なのか？これは「不偏分散」と呼ばれる調整で、母分散の推定に偏りが出ないようにするためです。
$$
\begin{eqnarray}
S^{2} &=& \frac{1}{n-1}\sum_{i=1}^{n}(X_{i} – \bar{X})^{2} \\
&=& \frac{1}{n-1}\sum_{i=1}^{n} \left[(X_{i} – \mu) – (\bar{X} – \mu) \right]^{2} \\
&=& \frac{1}{n-1}\left[\sum_{i=1}^{n}(X_{i} – \mu)^{2} -2(\bar{X} – \mu)\sum_{i=1}^{n}(X_i – \mu) +\sum_{i=1}^{n}(\bar{X}-\mu)^{2} \right]\\
&=& \frac{1}{n-1}\left[\sum_{i=1}^{n}(X_i – \mu)^{2} – n(\bar{X} – \mu)^{2} \right]
\end{eqnarray}
$$
$$
\begin{eqnarray}
E[S^{2}] &=& \frac{1}{n-1}\left[\sum_{i=1}^{n}E[(X_{i} – \mu)^{2}] -nE[(\bar{X} – \mu)^{2}]\right] \\
&=& \frac{n-1}{n-1}\sigma^{2}\\
&=& \sigma^{2}
\end{eqnarray}
$$
これより、\(S^{2}\)の期待値は\(\sigma^2\)となるので、分母がn-1とします。
標本分布とは何か？
標本平均や標本分散は、標本を取るたびに値が変わります。つまり、標本平均そのものが「確率変数」なのです。
この「標本平均の分布」こそが 標本分布 (sampling distribution) です。
母集団 → 標本抽出 → 標本平均 → 繰り返す → 標本分布
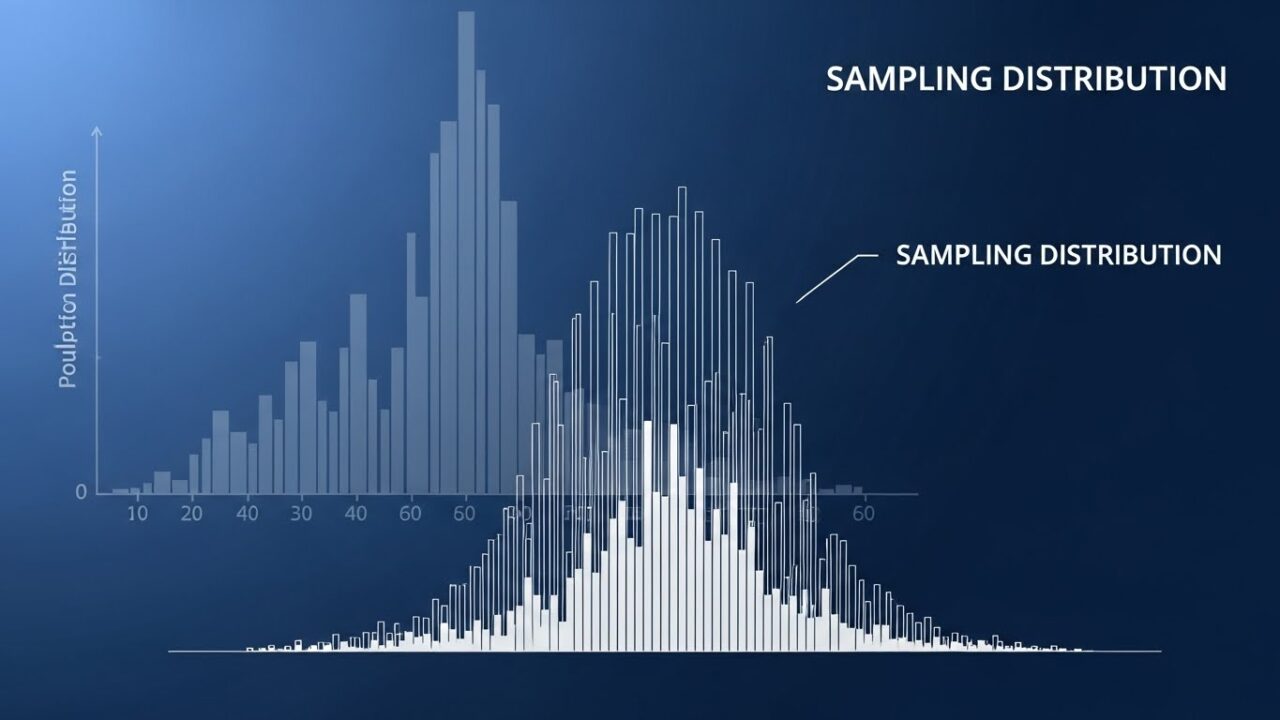
標本分布のヒストグラム
母集団を平均170、分散25の正規分布とし、標本サイズ30で1000回抽出した標本平均の分布をシミュレーションしました。
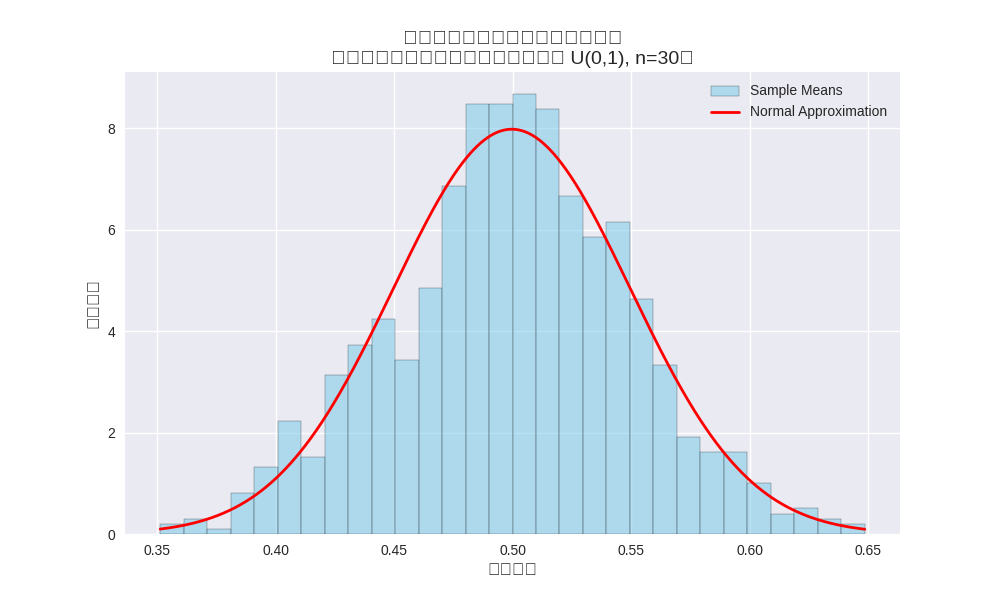
赤い破線が母平均を示しています。標本平均の分布が母平均を中心に集まっていることがわかります。
標本分布と中心極限定理
統計学で最も重要な定理のひとつが 中心極限定理 です。
- 母集団の分布がどんな形でも、標本サイズ n が十分大きければ、標本平均の分布は正規分布に近づく。
数式で表すと：
\[\bar {X}\sim N\left( \mu ,\frac{\sigma ^2}{n}\right)\]
この性質のおかげで、統計学では正規分布を前提とした推定や検定が広く使えるのです。
標本分散の分布
標本分散も確率変数です。標本分散の分布は「カイ二乗分布」に従います。
\[\frac{(n-1)S^2}{\sigma ^2}\sim \chi _{n-1}^2\]
この性質は、母分散の推定や分散分析 (ANOVA) の基礎になります。
標本分布の応用
標本分布を理解すると、次のような応用が可能になります。
- 信頼区間の構築
標本平均の分布を使って母平均の範囲を推定する。 - 仮説検定
標本平均の分布を基に「母平均がある値かどうか」を検証する。 - 分散分析
標本分散の分布を利用して、グループ間の差を検証する。
まとめ
統計学の基礎である「標本分布」は、母集団から抽出した標本によって計算される統計量（標本平均や標本分散）が、繰り返し抽出することでどのような分布を持つかを示す概念です。
- 標本平均は母平均の推定量であり、その期待値は母平均に一致し、分散は母分散を標本サイズ n で割ったものになります。標本サイズが大きくなるほどばらつきは小さくなり、母平均に近づいていきます。
- 標本分散は「不偏分散」として定義され、母分散の推定に偏りが出ないよう調整されています。その分布はカイ二乗分布に従い、分散分析や仮説検定の基礎となります。
- 中心極限定理により、母集団の分布がどのような形であっても、標本サイズが十分大きければ標本平均の分布は正規分布に近づきます。この性質が統計学における推定や検定の理論的な支えとなっています。
標本分布を理解することで、信頼区間の構築や仮説検定、分散分析など、統計学の応用的な手法を正しく使えるようになります。最初は抽象的に感じるかもしれませんが、数式と図解を組み合わせて考えることで直感的に理解でき、統計学の学習を進めるうえで大きな助けとなるでしょう。
![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/4aa03195.892069bb.4aa03196.39df6be9/?me_id=1213310&item_id=10335792&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F0655%2F9784130420655.jpg%3F_ex%3D300x300&s=300x300&t=picttext "[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]")
