臨床試験における多重比較法 ― グラフィカルアプローチの魅力と実践
記事の目次
Toggleはじめに
臨床試験では複数の評価項目(主要評価項目、副次評価項目)が設定されることが一般的です。これらを同時に検定すると「多重性の問題」が生じ、第一種過誤率(Familywise Error Rate; FWER)の制御が必須となります。従来はBonferroni法やHolm法といった古典的手法が用いられてきましたが、近年はゲートキーピング法やグラフィカルアプローチが注目されています。
本稿では、グラフィカルアプローチの考え方と実務的な応用について解説します。
以下の記事ではゲートキーピング法についての記事となりますので、興味がある方は是非ご一読ください。

グラフィカルアプローチとは?
グラフィカルアプローチ(Graphical Approach)は、Bretzら(2009)によって体系化された多重比較法です。特徴は以下の通りです。
- 有意水準の分配と再分配を「グラフ」で表現
- 各仮説をノード(頂点)、有意水準の流れをエッジ(矢印)として可視化
- ゲートキーピング法を一般化し、柔軟に設計可能
つまり、複雑な階層構造や優先順位を持つ仮説群を、直感的に理解できる「図解」に落とし込む手法です。
基本構造
グラフィカルアプローチでは、以下の要素を定義します。
- ノード(Node): 各帰無仮説 \(H_i\) を表す。
- 重み(Weight): 各ノードに割り当てられる初期有意水準 \(\alpha _i\)。
- エッジ(Edge): 棄却された仮説から他の仮説へ有意水準を再分配するルール。
数式表現
初期状態では次を満たします:
\[\sum _{i=1}^K\alpha _i=\alpha\]
仮説 \(H_i\) が棄却された場合、その有意水準 \(\alpha _i\) はエッジの重みに従って他の仮説へ分配されます。例えば、ノード i からノード j へのエッジの重みを \(g_{ij}\) とすると、
\[\alpha _j\leftarrow \alpha _j+g_{ij}\cdot \alpha _i\]
となります。ここで、各ノードから出るエッジの重みは次を満たします:
\[\sum _jg_{ij}\leq 1\]
図解で理解するグラフィカルアプローチ
例:主要評価項目と副次評価項目
臨床試験で「主要評価項目(Primary)」と「副次評価項目(Secondary)」がある場合を考えます。
- 初期有意水準: \(\alpha =0.05\)
- 割り当て: 主要評価項目に \(\alpha _1=0.04\)、副次評価項目に \(\alpha _2=0.01\)
図で表すと以下のようになります。
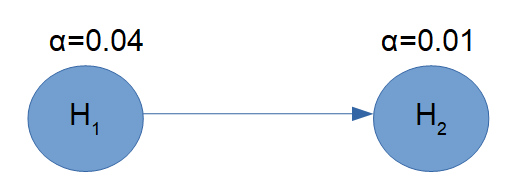
- H1が棄却されれば、その0.04の一部(例えば全て)をH2に再分配。
- H1が棄却されなければ、H2は0.01でのみ検定。
このように、主要項目が成功した場合に副次項目へ有意水準を「譲渡」する構造を直感的に表現できます。
実務での応用例
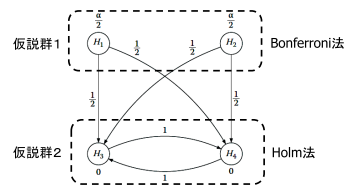
並列型ゲートキーピング
複数の主要評価項目がある場合、それぞれをノードとして並列に配置し、成功したものから副次項目へ有意水準を流すことができます。
樹木型ゲートキーピング
主要項目が複数あり、それぞれが異なる副次項目に接続する場合は「樹木型」のグラフになります。
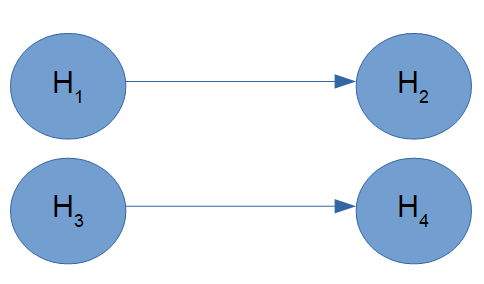
- 直感的な可視化: 有意水準の流れを矢印で表すため、規制当局や臨床チームに説明しやすい。
- 柔軟性: 固定順序法やHolm法を含む多くの手法を包含。
- 拡張性: グループ逐次デザインや適応デザインにも応用可能。
数式と図解による具体例
例:3つの仮説
仮説 \(H_1,H_2,H_3\) に初期有意水準を次のように割り当てます。
\(\alpha _1=0.03,\quad \alpha _2=0.01,\quad \alpha _3=0.01\)
再分配ルール:
- \(H_1\) が棄却されたら、その0.03を \(H_2\) と \(H_3\) に等分配。
- \(H_2\) が棄却されたら、その0.01を \(H_3\) に全て渡す。
図で表すと:
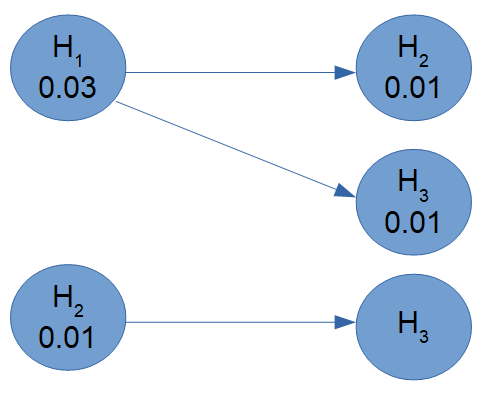
この構造により、主要項目が成功すれば副次項目の検出力が高まる仕組みになります。
規制当局の視点
FDAやEMAのガイダンスでは、主要評価項目だけでなく副次評価項目もFWER制御の対象とすることが求められています。グラフィカルアプローチはその要請に応える方法として有力であり、承認審査でも説明可能な「透明性の高い手法」として評価されています。
まとめ
臨床試験における多重性の問題は、薬効の信頼性や承認審査の妥当性に直結する重要な課題です。特に、主要評価項目と副次評価項目が階層的に構造化された試験では、FWERの厳密な制御が求められます。
グラフィカルアプローチは、こうした複雑な検定構造を「視覚的に設計・説明できる」革新的な手法です。仮説ごとの有意水準の分配と再分配をノードとエッジで表現することで、検定手順の透明性と柔軟性を両立させます。さらに、ゲートキーピング法や階層手順、Holm法など従来の手法を包含し、適応デザインやグループ逐次デザインにも拡張可能です。
規制当局もこの手法を高く評価しており、FDAやEMAのガイダンスでもその有用性が明示されています。実務においては、統計家が試験設計段階からグラフィカルアプローチを活用することで、より合理的かつ説明可能な検定戦略を構築できるでしょう。
今後の臨床試験では、グラフィカルアプローチが多重比較の標準的な選択肢となることが期待されます。視覚的に明快で、理論的にも強固なこの手法は、統計家と規制当局、そして医療現場をつなぐ架け橋となるのです。