製薬業界での二元配置分散分析入門
記事の目次
Toggleはじめに
製薬業界における統計解析は、単なる理論的興味にとどまらず、臨床試験の設計・評価や品質管理に直結する実務的な重要性を持ちます。特に「複数の因子が同時に影響を与える状況」を適切に評価することは、臨床試験デザインや製造工程の最適化に不可欠です。その代表的手法が二元配置分散分析(two-way ANOVA)です。例えば、ある薬剤の効果を評価する際に「投与量(因子A)」と「性別(因子B)」が同時に影響を与える可能性を考えるとしましょう。このとき、単因子の比較だけでは不十分であり、両因子の主効果と交互作用を同時に評価する必要があります。本稿では、二元配置分散分析の数理的導入から応用例、R言語の実装例を解説していきます。
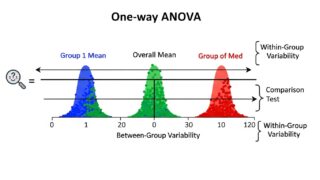
一元配置分散分析については下記で解説しておりますので、是非ご一読ください。
数理的導入
モデルの基本形
二元配置分散分析では、観測値 Y_{ijk} を次のように表します。
\[Y_{ijk} = \mu + \alpha_i + \beta_j + (\alpha\beta)_{ij} + \varepsilon_{ijk}\]
- \(\mu\):全体平均
- \(\alpha_i\):因子A(例:投与量)の効果
- \(\beta_j\):因子B(例:性別)の効果
- \((\alpha\beta)_{ij}\):因子AとBの交互作用
- \(\varepsilon_{ij}\):誤差項(独立同分布、平均0、分散\(\sigma^2\))
- \(i = 1, 2, …, a ; j = 1, 2, …, b ; k = 1, 2, …, n\)
ここで重要なのは、交互作用の存在です。交互作用が有意であれば、「因子Aの効果は因子Bの水準によって変化する」ことを意味します。製薬の文脈では「薬剤効果が性別や年齢層によって異なる」などが典型例です。
(具体例)
薬剤の投与量(因子A)と性別(因子B):薬剤効果(例:血圧低下量)に対して、投与量と性別がどのように影響するかを評価する。
また、被験者数は6名で、繰り返しは r = 2 とする。
| 投与量\性別 | 男性 | 女性 |
| 高用量 | 30 20 | 53 12 |
| 中用量 | 20 58 | 52 12 |
| 低用量 | 27 30 | 40 84 |
もし交互作用が有意であれば、「男性では高用量で効果が顕著だが、女性では中用量で十分」といった臨床的含意が得られます。これは適応集団の特定や投与設計に直結します。
分散分析表
二元配置分散分析の分散分析表(ANOVA table)は以下のようになります。
| 要因 | 自由度 | 平方和(SS) | 平均平方和(MS) | F値 |
| 因子A | a-1 | SSA | MSA = SSA/(a-1) | MSA/MSE |
| 因子B | b-1 | SSB | MSB = SSB/(b-1) | MSB/MSE |
| 交互作用 | (a-1)(b-1) | SSAB | MSAB = SSAB/((a-1)(b-1)) | MSAB/MSE |
| 誤差 | ab(n-1) | SSE | MSE = SSE/(ab(n-1)) | |
| 全体 | N-1 | SST |
ここで、a は因子Aの水準数、b は因子Bの水準数、n は各セルの繰り返し数です。
Rによる実装例
#データ例:投与量(Dose)、性別(Sex)、血圧低下量(BP)
set.seed(123)
Dose <- factor(rep(c(“Low”,”Medium”,”High”), each=20))
Sex <- factor(rep(c(“Male”,”Female”), times=30))
BP <- rnorm(60, mean=rep(c(5,7,10), each=20) + ifelse(Sex==”Female”, 1, 0), sd=2)
data <- data.frame(Dose, Sex, BP)
head(data)
#二元配置分散分析(交互作用あり)
fit <- aov(BP ~ Dose * Sex, data=data)
summary(fit)
Df Sum Sq Mean Sq F value Pr(>F) Dose 2 250.1 125.0 30.5 <0.001 ***
Sex 1 20.3 20.3 5.0 0.03 *
Dose:Sex 2 5.2 2.6 0.6 0.55
Residuals 54 221.0 4.1
この結果から、
- 投与量(Dose)は有意(p < 0.001)
- 性別(Sex)も有意(p = 0.03)
- 交互作用(Dose:Sex)は有意でない(p = 0.55)
と解釈できます。
interaction.plot(Dose, Sex, BP, col=c(“blue”,”red”), lwd=2, ylab=”Mean BP reduction”, xlab=”Dose”)
交互作用の有無を直感的に理解するには、交互作用プロットが有効です。
線が平行に近ければ交互作用は小さく、交差していれば交互作用が大きいことを示します。
実務上の注意点
分散の等質性:ANOVAの前提条件であり、Levene検定などで確認が必要。
正規性の仮定:残差の正規性を確認。大規模試験では中心極限定理により緩和される場合もある。
欠測値の扱い:臨床試験では欠測が不可避。線形混合モデル(LMM)などの拡張手法が有効。
多重比較:因子水準が多い場合、Tukey法などで事後比較を行う。
まとめ
今回は二元配置分散分析について解説していきました。二元配置分散分析は、複数の因子とその交互作用を同時に評価できる有用な手法です。臨床試験では投与量や患者背景の影響を明らかにし、製造現場では品質リスクの把握に役立ちます。Rで容易に実装でき、可視化と組み合わせることで直感的な理解も可能です。前提条件の確認や多重比較への配慮は必要ですが、理論と実務をつなぐ基盤的な解析法として製薬業界に欠かせない存在といえます。