はじめに
臨床試験において新しい治療法を評価する際、必ずしも「既存治療より優れている」ことを証明する必要はありません。ときに「既存治療と比べて臨床的に意味のある差がない」ことや「既存治療より劣っていない」ことを示すことが目的となります。これが同等性試験と非劣性試験です。
これらの試験は、患者にとって新しい治療法が「十分に有用である」ことを確認するために重要ですが、試験の設計において最も悩ましいのが必要症例数の算定です。症例数が少なすぎれば信頼性が損なわれ、多すぎれば倫理的・経済的に負担が大きくなります。本稿では、非劣性試験と同等性試験における症例数設計の基本的な考え方を、数式や図式を交えながら解説します。
非劣性試験と同等性試験
非劣性試験 (Non-inferiority trial)
新しい治療法が既存治療より「臨床的に意味のある範囲で劣っていない」ことを示す試験。
例：既存薬の有効率70%、新薬が65%以上なら許容できる → 非劣性マージン δ = -0.05。
同等性試験 (Equivalence trial)
新しい治療法が既存治療と「臨床的に意味のある差がない」ことを示す試験。
例：有効率差が ±7%以内なら同等とみなす → 同等性マージン = [-0.07, +0.07]。
非劣性試験、同等性試験を図式にすると以下のようになります。
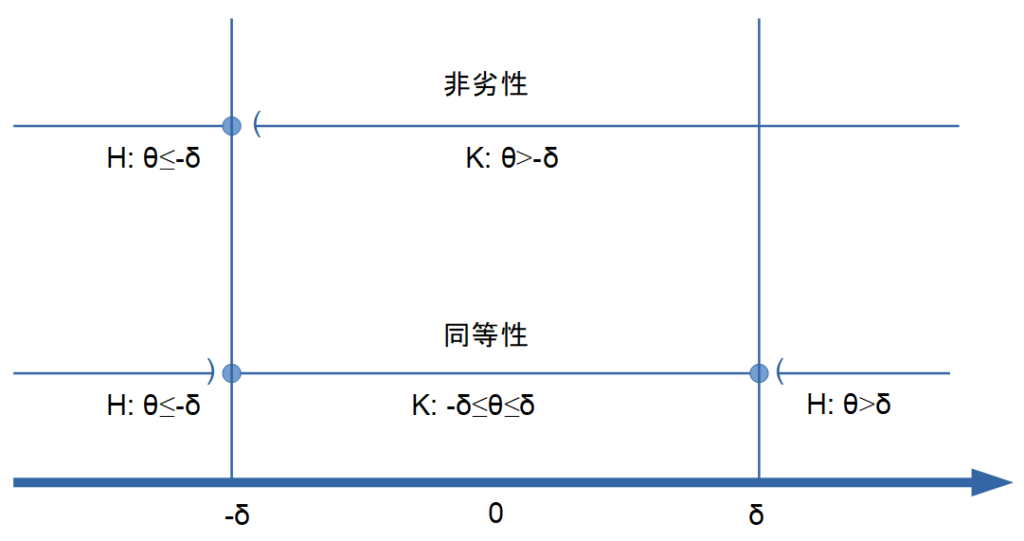
- 信頼区間の下限が -δ を超えれば「非劣性」と判断
- 信頼区間全体が [-δ, +δ] に収まれば「同等」と判断
非劣性試験と非劣性マージンについて下記記事で紹介しておりますので、興味がある方は是非ご一読ください。
非劣性試験のサンプルサイズ
仮説設定
非劣性試験の仮説設定は以下となります。
\[H_0:\mu _{\mathrm{new}}-\mu _{\mathrm{control}} \leq -\delta\]
\[H_1:\mu _{\mathrm{new}}-\mu _{\mathrm{control}} > -\delta\]
サンプルサイズの設定
仮説設定の式っを見てみると、下記記事の片側検定の仮説\(\mu_0\)を\(\mu_0 – \delta\)に置き換えた仮説であることがわかります。したがって、症例数の設定は片側検定の方法がそのまま応用できます。
有意水準\(\alpha\)について、\(\sigma^{2}\)が既知で、
\[\frac{\sqrt{n}(\bar{x} – \mu_{0} + \delta)}{\sigma} \geq z(1-\alpha)\]
の時、帰無仮説\(H_0\)を棄却し、対立仮説\(H_1\)を採択すると判断し、必要な症例数は、
\[n \geq \left(\frac{\sigma}{\Delta + \delta} \right)^{2}(z(1-\alpha) + z(\beta_0))^{2}\]
となります。ただし、\(\Delta = \mu – \mu_0\)
同等性試験のサンプルサイズ
同等性試験の仮説設定は以下となります。
\[H_0:|\mu _{\mathrm{new}}-\mu _{\mathrm{control}}|\geq \delta\]
\[H_1:|\mu _{\mathrm{new}}-\mu _{\mathrm{control}}|<\delta\]
\(\theta = \mu _{\mathrm{new}}-\mu _{\mathrm{control}}\)として、この仮説はさらに二つの仮説と表すことができます。
\[H_{01}: \theta \leq – \delta \; H_{11}: \theta > – \delta\]
\[H_{02}: \theta \leq \delta \; H_{12}: \theta > \delta\]
また、\(\theta \geq – \delta\) または\(\theta \leq \delta\)を棄却するには帰無仮説\((H_{01},H_{02})\)の両方を有意水準\(\alpha\)で棄却しなければならないこと、その際用いる検定統計量が次のように与えられます。
\(([H_{01},[H_{11})\)の検定の時には、
\[T_1(x) = \frac{\sqrt{n}(\bar{x} – \mu_{0} + \delta)}{\sigma}\]
を用いります。\(T_1(x) \geq z(1- \alpha)\)のとき、\(H_{01}\)を棄却する検定が有意水準\(\alpha\)となります。
\((H_{02},H_{12})\)の検定の時には、
\[T_2(x) = \frac{\sqrt{n}(\bar{x} – \mu_{0} – \delta)}{\sigma}\]
を用いります。\(T_2(x) \leq – z(1- \alpha)\)のとき、\(H_{02}\)を棄却する検定が有意水準\(\alpha\)となります。
ここで同等性検定の検出力関数を求めていきます。二つの帰無仮説\(H_{01},H_{02}\)をともに棄却する棄却域は以下のように表すことができます。
$$
\begin{align}
[T_1(x) \geq z(1-\alpha)] \cap [T_2(x) \leq -z(1-\alpha)]
&= \left[ \frac{\sqrt{n}(\bar{x} – \mu)}{\sigma}
\geq z(1-\alpha) – \frac{\sqrt{n}(\Delta + \delta)}{\sigma} \right] \\
&\quad \cap \left[ \frac{\sqrt{n}(\bar{x} – \mu)}{\sigma}
\leq -z(1-\alpha) – \frac{\sqrt{n}(\Delta – \delta)}{\sigma} \right] \\
&= \left[\, z(1-\alpha) – \frac{\sqrt{n}(\Delta + \delta)}{\sigma}
\leq \frac{\sqrt{n}(\bar{x} – \mu)}{\sigma}
\leq -z(1-\alpha) – \frac{\sqrt{n}(\Delta – \delta)}{\sigma} \,\right]
\end{align}
$$
よって検出力関数は次式で与えられます。
\[\beta(\mu) = \Phi \left(-z(1-\alpha) – \frac{\sqrt{n}(\Delta – \delta)}{\sigma} \right) – \Phi \left(z(1-\alpha) – \frac{\sqrt{n}(\Delta + \delta)}{\sigma} \right)\]
関係式\(\Phi(-x) = 1- \Phi(x) \)を利用して、
\[\beta(\mu) = \Phi \left(\frac{\sqrt{n}(\delta – \Delta)}{\sigma} -z(1-\alpha) \right) + \Phi \left(\frac{\sqrt{n}(\Delta + \delta)}{\sigma} – z(1-\alpha) \right)\]
今、\(A = \Phi \left(\frac{\sqrt{n}(\delta – \Delta)}{\sigma} -z(1-\alpha) \right)\), \(B = \Phi \left(\frac{\sqrt{n}(\delta + \Delta)}{\sigma} -z(1-\alpha) \right)\), \(C = 2 \Phi \left(\frac{\sqrt{n}(\delta – |\Delta|)}{\sigma} -z(1-\alpha) \right) \)とおく。
- \(\Delta > 0 \)の時、A<B, C= 2Aから、A+B>Cが成り立ちます。
- \(\Delta \leq 0 \)の時、A>B, C= 2Bから、A+B>Cが成り立ちます。
よって、検出力関数に対して次の不等式が成り立ちます。
$$
\begin{eqnarray}
\beta(\mu) &=& A+B -1 > C-1\\
&=& 2 \Phi \left(\frac{\sqrt{n}(\delta – |\Delta|)}{\sigma} -z(1-\alpha) \right) – 1
\end{eqnarray}
$$
したがって、検出力を\(\beta_0\)以上に設定した際の必要な症例数nは、
\[\left[2 \Phi \left(\frac{\sqrt{n}(\delta – |\Delta|)}{\sigma} -z(1-\alpha)\right) – 1 \right] \geq \beta_0\]
をnについて解けばよいので、
\[n \geq \left[ z(1-\alpha) + z(1-\frac{\beta_0}{2}) \right]^{2} \left[\frac{\sigma}{(\delta – |\Delta|)}\right]^{2}\]
実例
同等性試験
同じ条件で同等性マージン = ±0.07。
両側検定のため必要症例数 ≈ 400例/群。
非劣性試験
既存薬成功率 = 0.60、新薬予測成功率 = 0.65、非劣性マージン = -0.05。
検出力80%、有意水準5% → 必要症例数 ≈ 300例/群。
規制当局の視点
PMDAやICH E9ガイドラインでは、マージン設定の臨床的根拠が最重要とされます。
- 非劣性マージンは「既存治療の効果の一部を保持する」観点で設定。
- 同等性マージンは「臨床的に意味のある差がない範囲」を事前に定義。
まとめ
非劣性試験と同等性試験は、いずれも新しい治療法の価値を示すために重要な役割を果たします。しかし、仮説の設定が異なるため、必要症例数にも違いが生じます。非劣性試験は片側検定であるため症例数は比較的少なく済みますが、同等性試験は両側検定であるためより多くの症例が必要となります。症例数は「マージン」「効果量」「有意水準」「検出力」に依存し、さらに規制当局はマージン設定の妥当性を厳しく評価します。したがって、試験設計においては統計的な要件と臨床的意義の両方を満たすよう慎重に症例数を決定することが不可欠です。
