1標本の群比較におけるサンプルサイズ設定
記事の目次
Toggleはじめに
臨床試験や製薬研究において「サンプルサイズの設定」は最も重要な設計要素の一つです。サ臨床試験や製薬研究において「サンプルサイズの設定」は、研究の信頼性と倫理性を左右する極めて重要な要素です。サンプルサイズが小さすぎれば、真に存在する効果を見逃してしまい、研究の成果が不十分となります。逆に大きすぎれば、不要なコストや被験者への過剰な負担を招きます。特に 1標本の群比較、すなわち「ある群の平均値が既知の基準値と異なるか」を検証する場面では、検出力(power)や棄却域(rejection region)の理解が不可欠です。
本記事では、1標本の群比較における基本的な検定の枠組みから、サンプルサイズの導出方法、検出力と棄却域の関係、さらにRによる計算例や図式を交えた直感的理解までを解説します。研究者や製薬業界の専門家が、より合理的で説得力のある試験設計を行うための基盤を提供することを目的としています。
1標本の群比較とは
仮説設定
ある母集団の平均値 \(\mu\) が既知の基準値 \(\mu _0\) と異なるかを検証します。
両側検定の場合
- 帰無仮説: \(H_0:\mu =\mu _0\)
- 対立仮説: \(H_1:\mu \neq \mu _0\)
片側検定の場合
- 帰無仮説: \(H_0:\mu \leq \mu _0\)
- 対立仮説: \(H_1:\mu > \mu _0\)
標本平均 \(\bar {X}\) を用いて検定統計量を構築します。
検定統計量と棄却域
標本サイズ \(n\)、母集団標準偏差 \(\sigma\) が既知とすると、検定統計量は
\[Z=\frac{\bar {X}-\mu _0}{\sigma /\sqrt{n}}\]
となり、帰無仮説下では標準正規分布 N(0,1) に従う。
棄却域
有意水準 \(\alpha\) の両側検定では、
\[|Z|>z_{1-\alpha /2}\]
を満たすとき帰無仮説を棄却する。ここで \(z_{1-\alpha /2}\) は標準正規分布の上側 \((1-\alpha /2)\) 分位点。
例えば \(\alpha =0.05\) の場合、棄却域は \(|Z|>1.96\)。
また、片側検定では、検定統計量は下記となります。
\[|Z|>z_{1-\alpha}\]\]
検出力(Power)の考え方
検出力とは「対立仮説が真のときに帰無仮説を正しく棄却できる確率」となります。
検出力は検出力は= 1 – P(第2種の誤り)とも言えます。
- 第1種の誤り確率:\(H_0\)が正しいとき、\(H_0\)を棄却するという誤り確率
- 第2種の誤り確率:\(H_0\)が正しくないとき、\(H_0\)を棄却しないという誤り確率
全ての\(\theta \in \Theta\)に対して、帰無仮説を棄却する確率、すなわち、
\[\beta(\theta)=P(T \in c)\]
を検出力関数といいます。ただし、cは棄却域
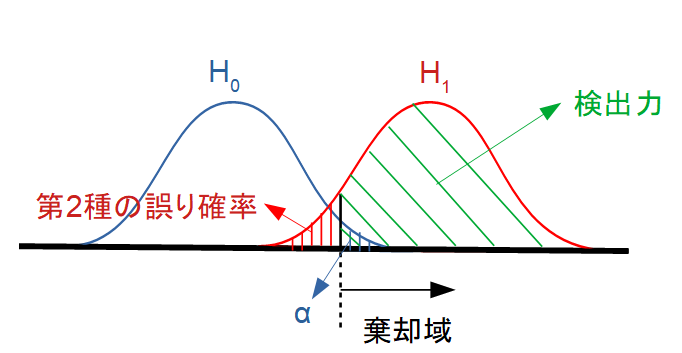
検出力や第2種の誤り確率の関係を図示すると以下のようになります。
サンプルサイズの導出
片側検定の場合を考えていきます。この仮説について有意水準\(\alpha\)の片側検定を行うには、
\[\frac{\sqrt{n}(\hat{x}-\mu_0)}{\sigma} \geq z(1 – \alpha)\]
のとき、\(H_0\)を棄却すると考えます。この時検出力関数は、
$$
\begin{eqnarray}
\beta(\mu) &=& P_{\mu} \left( \frac{\sqrt{n}(\hat{x}-\mu_0)}{\sigma} \geq z(1 – \alpha) \right)\\
&=& 1 – \Phi \left( z(1 – \alpha) – \frac{\sqrt{n}(\mu-\mu_0)}{\sigma} \right)\\
&=& \Phi \left( \frac{\sqrt{n}(\mu-\mu_0)}{\sigma} – z(1 – \alpha) \right) , (\mu > \mu_{0})
\end{eqnarray}
$$
で与えられます。よって検出力がある値\(\beta_{0}\)(一般的に80% ~ 90%)以上であるためには、
\[\Phi \left( \frac{\sqrt{n}(\mu-\mu_0)}{\sigma} – z(1 – \alpha) \right) \geq \beta_0\]
が成り立たなければなりません。\(z(\beta_0)\)を標準正規分布の\(\beta_0\)パーセンタイルとすると、
\[\frac{\sqrt{n}(\mu-\mu_0)}{\sigma} – z(1 – \alpha) \geq z(\beta_0)\]
が得られます。この式を\(n\)について解くと、
\[n \geq \left(\frac{\sigma}{\Delta} \right)^2 (z(1-\alpha) + z(\beta_0))^{2}\]
ただし、\(\Delta = \mu – \mu_0 > 0\)
ここで、\(\Delta\) は新しいtreatment効果\(\mu\) と既存効果\(\mu_0\)の差となります。
得られた式から\(\Delta\)が大きいほど症例数nは少なくて済み、\(\Delta\)が小さいほど多くの症例が必要となることがわかります。
通常\(\Delta\)の値は臨床的観点から、既存効果\(\mu_0\)と比べて新しいtreatment効果\(\mu\)が\(\Delta\)だけ上回ったとき、臨床的に有意義であると考えられる最小の値に設定されます。
Rによる計算例
例えば、母標準偏差 \(\sigma =10\)、効果量 \(\Delta =5\)、有意水準 \(\alpha =0.05\)、検出力 \(1-\beta =0.8\) の場合。
alpha <- 0.05
beta <- 0.2
sigma <- 10
delta <- 5
z_alpha <- qnorm(1 – alpha/2)
z_beta <- qnorm(1 – beta)
n <- ((z_alpha + z_beta) * sigma / delta)^2
n
解釈:\(n \approx 25.3\)とすると、少なくとも必要なサンプル数は26例となります。
臨床試験での応用
製薬分野では、基準値(例:プラセボ群の既知平均、あるいは規制当局が定める閾値)と比較する場面が多いです。
- PMDAやFDAのガイドラインでは、検出力80%以上を推奨するケースが多い。
- サンプルサイズは倫理的配慮からも重要であり、過剰な被験者負担を避けつつ、十分な検出力を確保する必要がある。
まとめ
1標本の群比較におけるサンプルサイズ設定は、単なる統計的計算にとどまらず、研究の科学的妥当性・倫理的配慮・規制要件を同時に満たすための戦略的判断です。
- 標本平均を基準値と比較することで、帰無仮説の妥当性を検証する。
- 棄却域は有意水準によって決まり、検出力は分布のシフト量に依存する。
- サンプルサイズは「有意水準」「検出力」「効果量」「標準偏差」によって決定される。
- 実務ではRなどの統計ソフトを用いて計算し、PMDAやFDAの推奨水準を満たすことが重要である。
本記事で紹介した数式や図式を活用すれば、検出力や棄却域の直感的理解が深まり、より説得力ある試験設計が可能になります。さらに、ベイズ的視点を取り入れることで、事前分布を用いた柔軟なサンプルサイズ設定も可能となり、今後の研究設計に新たな展望を与えるでしょう。