区間推定入門:数式と図解で理解する信頼区間の世界
記事の目次
Toggleはじめに
統計学を学ぶ上で「推定」は避けて通れないテーマです。母集団の平均や割合を知りたいけれど、全員を調べることは現実的に不可能。そこで標本を用いて母集団の性質を推定します。その推定方法には大きく分けて 点推定 と 区間推定 があり、本記事では区間推定を中心に解説します。
区間推定は「母集団の真の値がこの範囲にあるだろう」と区間を提示する方法です。例えば「母平均は95%の確率で 50〜55 の間にある」といった形で表現されます。これにより、単なる点推定よりも信頼性を持って母集団の性質を議論できます。
点推定と区間推定の違い
- 点推定:母平均を推定する際、標本平均\( \bar {x}\) をそのまま推定値とする。
- 区間推定:標本平均の周囲に「誤差範囲」を設け、母平均が含まれる可能性の高い区間を提示する。
信頼区間の基本概念
区間推定でよく使われるのが 信頼区間 (Confidence Interval, CI) です。
母平均 \(\mu\) の信頼区間は次のように表されます:
\[\bar {x}\pm z_{\alpha /2}\cdot \frac{\sigma }{\sqrt{n}}\]
- \(\bar {x}\):標本平均
- \(\sigma\) :母標準偏差
- \(n\):標本サイズ
- \(z_{\alpha /2}\):標準正規分布の上側 \(\alpha /2\) 点の値
ここで「信頼係数 1-\(\alpha\) 」が重要です。例えば信頼係数 95% の場合、\(\alpha\) =0.05、つまり「95%の確率で母平均が区間に含まれる」と解釈します。
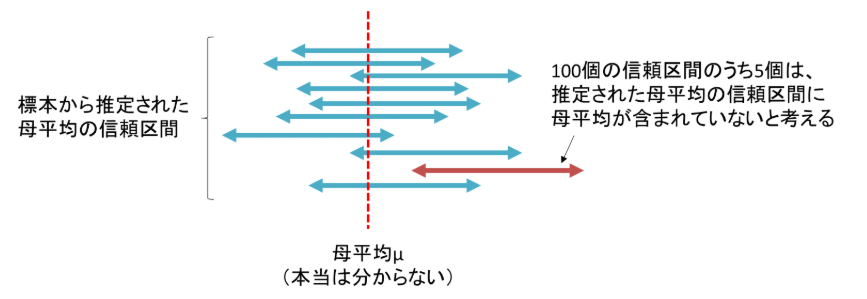
注意すべき点として、信頼区間は「母集団から標本を取ってきて、その平均から95%信頼区間を求める、という作業を100回やったときに、95回はその区間の中に母平均が含まれる」という”頻度”もしくは”割合”を意味します。
母標準偏差が既知の場合
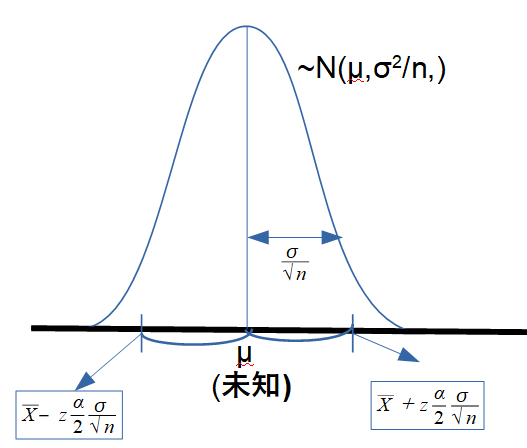
母標準偏差 \(\sigma\) が既知であると仮定すると、母平均の信頼区間は次の式で表されます:
\[CI=\left[ \bar {x}-z_{\alpha /2}\cdot \frac{\sigma }{\sqrt{n}},\; \bar {x}+z_{\alpha /2}\cdot \frac{\sigma }{\sqrt{n}}\right]\]
例
- 標本平均 \(\bar {x}=100\)
- 母標準偏差 \(\sigma =15\)
- 標本サイズ \(n=25\)
- 信頼係数 95% → \(z_{0.025}=1.96\)
計算すると:
\[CI=[100-1.96\cdot \frac{15}{5},\; 100+1.96\cdot \frac{15}{5}]\]
\[CI=[94.12,105.88]\]
つまり「母平均は95%の確率で 94.12〜105.88 の間にある」と推定できます。
母標準偏差が未知の場合
現実には母標準偏差 \(\sigma\) が未知であることが多いです。その場合、標本標準偏差 s を用い、t分布を使って信頼区間を構築します。
\[CI=\left[ \bar {x}-t_{\alpha /2,\; n-1}\cdot \frac{s}{\sqrt{n}},\; \bar {x}+t_{\alpha /2,\; n-1}\cdot \frac{s}{\sqrt{n}}\right]\]
ここで\( t_{\alpha /2,\; n-1}\) は自由度 \(n-1\) の t分布の上側 \(\alpha /2\) 点です。
母比率の区間推定
母比率 p の推定も重要です。例えば「新薬が有効だった患者の割合」を推定する場合です。
標本比率 \(\hat {p}=\frac{x}{n}\) を用いて次のように表します:
\[CI=\left[ \hat {p}-z_{\alpha /2}\cdot \sqrt{\frac{\hat {p}(1-\hat {p})}{n}},\; \hat {p}+z_{\alpha /2}\cdot \sqrt{\frac{\hat {p}(1-\hat {p})}{n}}\right]\]
以下では母比率の信頼区間の導出していきます。
\(X_i\)をベルヌーイ分布Ber(p)に従うとします。
\(X = X_1 + \cdots + X_n\)とすると、Xは二項分布Bi(np,np(1-p))に従います。
中心極限定理を用いて、
$$
\begin{eqnarray}
Z &=& \frac{(X_1 + \cdots + X_n) – E(X_1 + \cdots + X_n)}{\sqrt{V(X_1 + \cdots + X_n)}} \\
&=& \frac{X – np}{\sqrt{np(1-p)}}\\
&=& \frac{\frac{X}{n} – p}{\sqrt{\frac{p(1-p)}{n}}}\\
&=& \frac{\hat{p} – p}{\sqrt{\frac{p(1-p)}{n}}} \approx N(0,1) (\text{nが十分大})
\end{eqnarray}
$$
\begin{eqnarray}
P \left( -z_{\alpha/2} < X < z_{\alpha/2} \right) \\
& \leftrightarrow & P\left(|X| < z_{\alpha/2} \right) = 1 – \alpha \\
& \leftrightarrow & X^2 < z_{\alpha/2}^2 \\
& \leftrightarrow & \left(\frac{\hat{p} – p}{\sqrt{\frac{p(1-p)}{n}}} \right)^2 < z_{\alpha/2}^2 \\
& \leftrightarrow & \frac{(\hat{p} – p)^2}{\frac{p(1-p)}{n}} < z_{\alpha/2}^2 \\
& \leftrightarrow & n(\hat{p} – p)^2 < z_{\alpha/2}^2 \, p(1-p) \\
& \leftrightarrow & (n + z_{\alpha/2}^2)p^2 – (2n\hat{p} + z_{\alpha/2}^2)p + n\hat{p}^2 < 0 \quad \text{—(i)} \\
\end{eqnarray}
この式はpの二次方程式のため、解\(\alpha , \beta\)を解の公式で求めていきます。
(i)の左辺=0の解が\(\alpha , \beta\)とすると、
$$
\begin{eqnarray}
p &=& \frac{\left(2n\hat{p} + z_{\alpha/2}^2\right) \pm \sqrt{(2n\hat{p} + z_{\alpha/2}^2)^2 – 4\left(n + z_{\alpha/2}^2\right)n \hat{p}^2}}{2\left(n + z_{\alpha/2}^2 \right)} \\
&=& \frac{\left(2n\hat{p} + z_{\alpha/2}^2\right) \pm \sqrt{4n^2\hat{p}^2 + 4n\hat{p}z_{\alpha/2}^2 + z_{\alpha/2}^4 – 4n^2\hat{p}^2 – 4n z_{\alpha/2}^2 \hat{p}^2}}{2\left(n + z_{\alpha/2}^2 \right)} \\
&=& \frac{n}{n+z_{\alpha/2}^2}\left(\hat{p} + \frac{z_{\alpha/2}^2}{2n} \;\pm\; z_{\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n} + \frac{z_{\alpha/2}^2}{4n^2}}\right)
\end{eqnarray}
よって、
\[P\Biggl(\frac{n}{\,n+z_{\alpha/2}^2\,}\left(\hat{p} + \frac{z_{\alpha/2}^2}{2n}- z_{\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n} + \frac{z_{\alpha/2}^2}{4n^2}}\right)< p <\frac{n}{\,n+z_{\alpha/2}^2\,}\left(\hat{p} + \frac{z_{\alpha/2}^2}{2n}+ z_{\alpha/2}\sqrt{\frac{\hat{p}(1-\hat{p})}{n} + \frac{z_{\alpha/2}^2}{4n^2}}\right)\Biggr)\]
ここで、nが十分大きいときに、極限より、
\[P\left(\hat{p} – z(\frac{\alpha}{2})\sqrt{\frac{\hat{p}(1-\hat{p})}{n}} < p < \hat{p} + z(\frac{\alpha}{2})\sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \right)\] = 1 – \alpha
よって、信頼係数が\(1-\alpha\)のpの近似信頼区間は
\[\left[\hat{p} – z(\frac{\alpha}{2})\sqrt{\frac{\hat{p}(1-\hat{p})}{n}} , \hat{p} + z(\frac{\alpha}{2})\sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \right]\]
Q.E.D
実務での応用
- 医薬品開発:新薬の効果を推定する際、母平均の差の信頼区間を提示することで「効果が統計的に有意か」を判断。
- マーケティング:顧客満足度調査で母比率の信頼区間を算出し、全体の傾向を把握。
- 品質管理:製品の平均寿命の信頼区間を求め、規格を満たしているかを確認。
まとめ
区間推定は、母集団の特性を「点」ではなく「範囲」で推定する方法であり、推定の不確実性を直感的に理解するための重要な考え方です。標本平均を中心に誤差範囲を設けることで、母平均や母比率が含まれる可能性の高い区間を提示できます。母標準偏差が既知の場合は正規分布を用い、未知の場合は標本標準偏差と t 分布を用いるのが基本です。また、標本サイズが大きいほど区間は狭くなり、推定の精度が高まります。信頼区間は「母平均が必ずこの区間にある」という意味ではなく、繰り返し標本を取ったときに一定割合(例えば95%)の区間が母平均を含むという考え方です。医薬品開発やマーケティング、品質管理など幅広い分野で活用され、推定の不確実性を可視化する強力なツールとなります。つまり区間推定は、統計的推論をより信頼できるものにするための基盤であり、初心者にとっても「推定の幅を持たせる」イメージを理解することが第一歩となります。











