p値を正しく理解する:統計学を勉強していく人のための基礎から応用まで

記事の目次
Toggleはじめに
統計学を学び始めると必ず出会うのが「p値」です。臨床試験の論文や製薬企業の報告書には「p < 0.05」という表記が頻繁に登場します。しかし、p値の意味を誤解している人は少なくありません。
「p値が小さい=薬は効く」「p値が大きい=薬は効かない」といった単純な理解は危険です。この記事では、p値の定義・直感的な理解・数式・図解・製薬業界での応用を体系的に解説します。
p値とは何か?
定義
p値とは、帰無仮説が正しいと仮定したときに、観測されたデータ以上に極端な結果が得られる確率です。
数式で表すと:
\[p=P(\mathrm{観測された統計量以上の極端な値}\mid H_0\mathrm{が真})\]
ここで
統計量:t値やカイ二乗値など、検定に用いる指標
\(H_0\):帰無仮説(例:薬に効果はない)
直感的なイメージ
例えば「新薬は既存薬と同じ効果しかない」という帰無仮説を立てます。もし臨床試験で新薬群の平均効果が既存薬より大きく出た場合、その差が偶然のばらつきで説明できるかを確率で表すのがp値です。
p値が大きい → 偶然でも起こりうる → 帰無仮説を棄却できない
p値が小さい → 偶然では説明しにくい → 帰無仮説を棄却
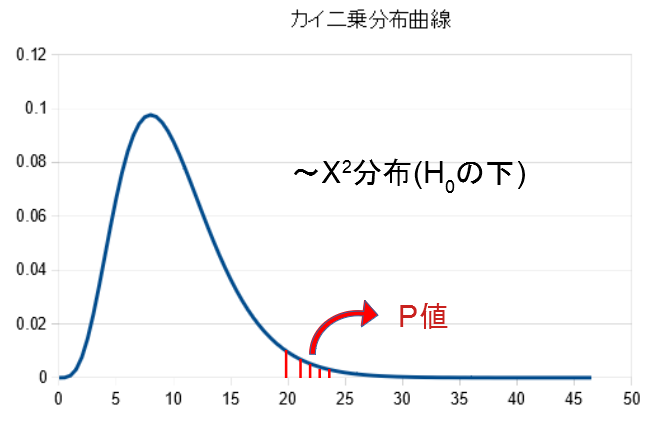
- 横軸:統計量(例:t値)
- 縦軸:確率密度
- 観測された統計量より「右側の面積」がp値
つまり、分布の裾野の面積がp値です。
p値の誤解と正しい理解
- p値は帰無仮説が正しい確率
- p値が0.05未満なら薬は必ず効く
- p値が大きいなら薬は効かない
- p値は「データが偶然で説明できるかどうかの指標」
- p値は「効果の大きさ」を示すものではない
- p値は「薬の有効性の確率」ではない
数式で見るp値の計算例
t検定の場合
2群の平均値差を検証するt検定では:
\[t=\frac{\bar {X}_1-\bar {X}_2}{\sqrt{\frac{s_1^2}{n_1}+\frac{s_2^2}{n_2}}}\]
- \(\bar {X}_1,\bar {X}_2\):平均値
- \(s_{1}^{2},s_{2}^{2}\):分散
- \(n_1,n_2\):サンプルサイズ
このt値を自由度に応じたt分布に当てはめ、裾野の面積を計算するとp値が得られます。
製薬業界での例
新薬群(n=100)の平均血圧低下量が10mmHg、既存薬群(n=100)が7mmHg、標準偏差が両群とも5mmHgとすると:
\[t=\frac{10-7}{\sqrt{\frac{25}{100}+\frac{25}{100}}}=\frac{3}{\sqrt{0.5}}\approx 4.24\]
自由度198のt分布でこの値を計算すると、p値は非常に小さく(<0.001)、帰無仮説は棄却されます。
p値の限界
サンプルサイズ依存性:
サンプルサイズが大きいと、わずかな差でもp値は小さくなります。逆にサンプルサイズが小さいと、大きな差でもp値は有意にならないことがあります。
効果の大きさを示さない:
p値は「差があるかどうか」を示すだけで、「どれくらい差があるか」は示しません。効果量や信頼区間と併用する必要があります。
製薬業界におけるp値の活用
臨床試験:新薬の有効性を検証する際に必須
規制当局:FDAやPMDAは「有意差の有無」だけでなく「臨床的意義」を重視
実務者の心得:p値だけで判断せず、効果量・安全性・臨床的意義を総合的に評価
まとめ
p値は統計学の中でも最も誤解されやすい概念のひとつですが、正しく理解すれば非常に強力な判断ツールになります。p値とは、「帰無仮説が正しいと仮定したときに、観測されたデータ以上に極端な結果が得られる確率」を示すものであり、薬の効果そのものや因果関係を直接示すものではありません。
製薬業界では、臨床試験の有意性判断にp値が用いられますが、p値が小さいからといって薬が“必ず効く”とは限らず、逆にp値が大きいからといって“まったく効果がない”とも言えません。重要なのは、p値を効果量や信頼区間と併せて解釈することです。
また、p値はサンプルサイズに依存するため、実務では「統計的有意性」と「臨床的意義」の両方を考慮する必要があります。規制当局(FDAやPMDA)も、単なるp値の大小だけでなく、薬の安全性や患者への実質的な利益を重視しています。
統計を学ぶ学生や社会人にとっても、p値は「データの意味を読み解く力」を養う第一歩です。グラフや数式を通じて直感的に理解し、誤解を避けながら活用できるようになることが、統計リテラシー向上への鍵となります。