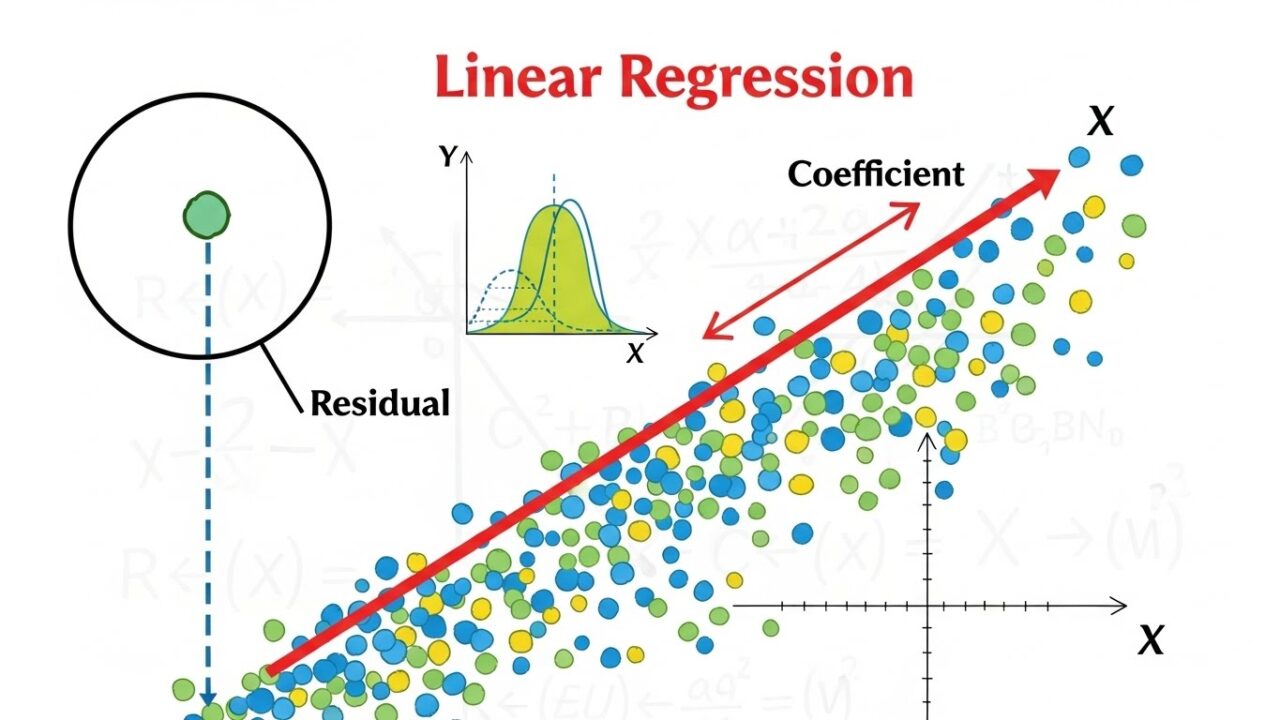
線形回帰の“本質”をつかむ― 係数・残差・モデル診断の読み方を深く理解する ―
記事の目次
Toggleはじめに
線形回帰は、統計学の中で最も基本的なモデルでありながら、実務での解釈には深い理解が求められます。
係数の意味、残差の読み方、多重共線性の影響など、単なる「当てはめ」ではなく、データの構造を理解するためのツールとして使いこなす必要があります。
この記事では、線形回帰の本質を
- 係数の読み方(単位あたりの変化)
- 残差プロットの意味
- 多重共線性(VIF)の直感的理解)
を中心に、図解を交えながら解説します。
線形回帰モデルの構造を直感的に捉える
線形回帰モデルは次の式で表されます。
\[Y=\beta _0+\beta _1X_1+\beta _2X_2+\cdots +\beta _pX_p+\varepsilon\]
ここで重要なのは、
回帰係数は「他の変数を一定にしたときの、Yの変化量」
を表すという点です。
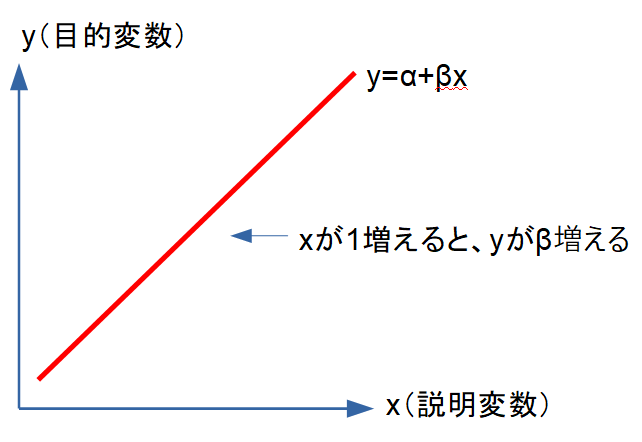
直線の傾きが β(回帰係数) です。
実務での読み方:単位あたりの変化をどう読むか?
例:広告費 → 売上
\[\mathrm{売上}=100+0.8\times \mathrm{広告費}\]
- 広告費が 1万円増えると売上が0.8万円増える
- ROI = 0.8(80%)
係数を“意思決定に使える形”に翻訳することが重要です。
残差プロットの“本当の意味”
残差とは、
\[e_i=y_i-\hat {y}_i\]
で表される、モデルが説明しきれなかった部分です。
残差プロットは、モデル診断の中で最も重要なツールです。
図解:理想的な残差プロット
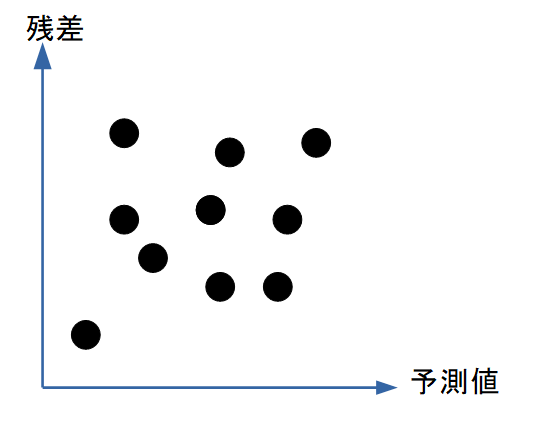
ランダムに散らばっている → 線形モデルが適切
図解:非線形性がある場合(U字型)
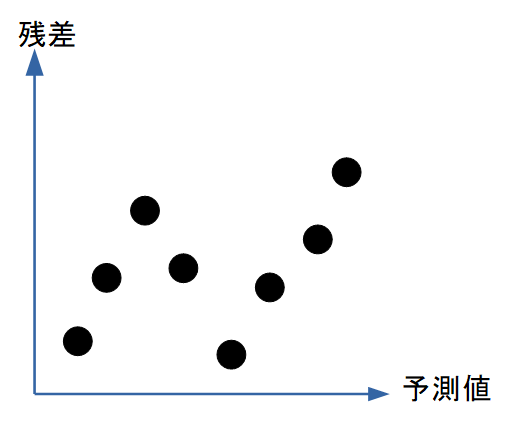
これは「線形では捉えきれない構造がある」というサイン。
→ 二次項\((X^2)\)やスプラインを追加すべき。
図解:分散不均一(heteroscedasticity)
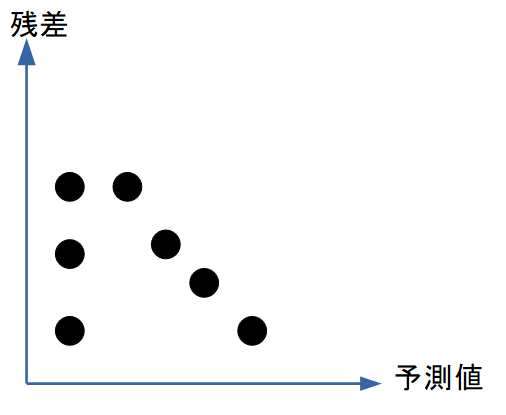
右に行くほど残差が広がる → 等分散性の仮定が破れている
→ 対数変換やWLSを検討。
図解:外れ値・影響点
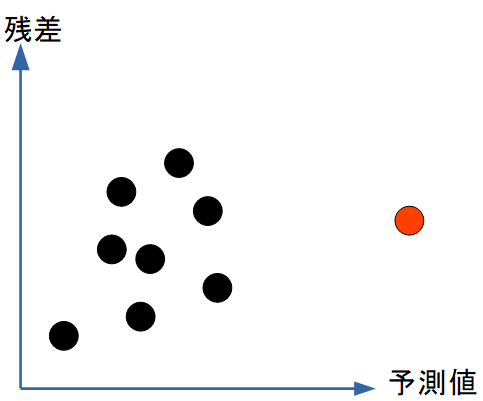
1点だけ極端に離れている場合(赤丸)、モデルの係数を大きく動かす危険な点です。
多重共線性の直感的理解
多重共線性とは、説明変数同士が強く相関している状態です。
\[\mathrm{VIF_{j}}=\frac{1}{1-R_j^2}\]
- R_j^2 が大きい(=他の変数で説明できる)
→ VIFが大きくなる
→ 係数が不安定になる
| VIF | 状態 |
| 1〜5 | 問題なし |
| 5〜10 | 注意 |
| 10以上 | 深刻な共線性 |
Rによる最小限の具体例
ここでは、1つ具体例を示します。
model <- lm(Sepal.Length ~ Sepal.Width + Petal.Length, data = iris)
# 残差プロット
plot(model$fitted.values, resid(model),
xlab = “Fitted values”, ylab = “Residuals”,
main = “Residual Plot”)
abline(h = 0, col = “red”)
# VIF
library(car)
vif(model)
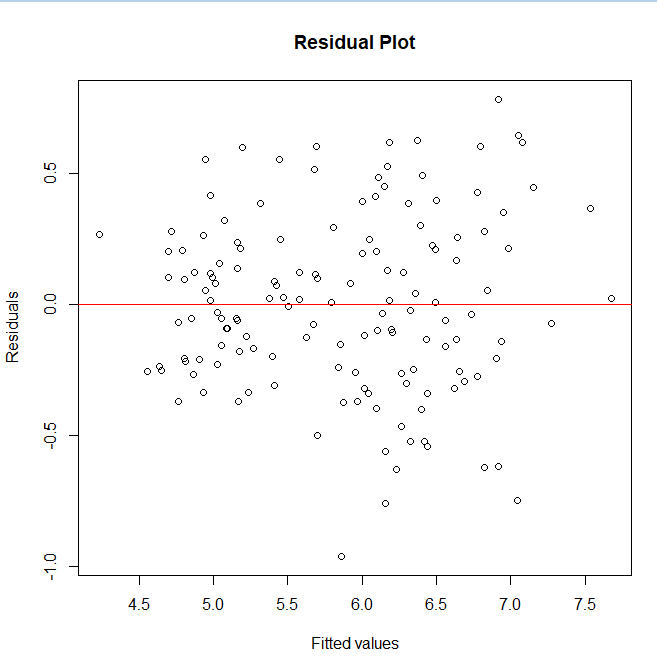
- Petal.Length の係数が大きい → 影響力が強い
- Sepal.Width と Petal.Length はやや相関 → VIFが上昇
- 残差プロットがランダム → 線形性は概ねOK
モデル診断の全体像
線形回帰の実務的な診断ポイントは次の5つです。
- 残差プロット
- 線形性・等分散性・外れ値を確認。
- 多重共線性(VIF)
- 係数の安定性を確認。
- 係数の解釈
- 単位あたりの変化、標準化係数、ROIなど。
- モデルの当てはまり
- \(R^2\)
- 調整済み \(R^2\)
- AIC / BIC
- 実務的妥当性
- モデルは意思決定に使えるか
- 変数の因果関係は妥当か
- 外れ値はデータエラーではないか
まとめ
線形回帰は、最も基本的な統計モデルでありながら、実務で使いこなすためには「係数」「残差」「多重共線性」という三つの視点を総合的に理解する必要があります。回帰係数は単なる数値ではなく、変数が1単位変化したときに目的変数がどの程度動くかを示す“実務的な意味”を持ちます。残差プロットは、モデルが見落としている構造を可視化し、線形性・等分散性・外れ値といった前提の妥当性を判断するための最も重要なツールです。また、多重共線性は係数の不安定さを生み、モデルの解釈を難しくするため、VIFを用いた診断が欠かせません。
これら三つの視点を組み合わせることで、線形回帰は単なる「当てはめの手法」から、データの構造を理解し、意思決定に活かすための強力な分析ツールへと変わります。線形回帰の本質は、数式そのものではなく、データの背後にある関係性を読み解くことにあります。こうした視点を身につけることで、より高度なモデル(GLM、LMM、機械学習)にも応用できる“統計的思考”が育ち、実務における分析の質が大きく向上します。


![[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。] [商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]](https://hbb.afl.rakuten.co.jp/hgb/4aa03195.892069bb.4aa03196.39df6be9/?me_id=1213310&item_id=13039446&pc=https%3A%2F%2Fthumbnail.image.rakuten.co.jp%2F%400_mall%2Fbook%2Fcabinet%2F8679%2F9784320018679_1_2.jpg%3F_ex%3D300x300&s=300x300&t=picttext)