モデル選択の基礎:AIC・BICを“情報量”として理解する— 過学習を避け、汎化性能を高めるための実務的ガイド —
記事の目次
Toggleはじめに
統計モデルや機械学習モデルを構築するとき、必ず直面するのが「どのモデルを選ぶべきか」という問題です。説明変数を増やせば精度は上がるように見える一方で、複雑にしすぎると過学習(overfitting)が起き、未知データでの性能が落ちてしまいます。
この“複雑さと汎化性能のトレードオフ”を定量的に評価するために生まれたのが、AIC(Akaike Information Criterion)とBIC(Bayesian Information Criterion)です。本記事では、これらを単なる「指標」ではなく、“情報量”として理解することを目指します。
AIC・BICとは何か
まずは定義から確認します。
● AIC(赤池情報量規準)
\[\mathrm{AIC}=-2\log L+2k\]
● BIC(ベイズ情報量規準)
\[\mathrm{BIC}=-2\log L+k\log n\]
- L:モデルの最大対数尤度
- k:推定パラメータ数
- n:サンプルサイズ
どちらも
「モデルの当てはまりの良さ(-2 log L)」と「モデルの複雑さ(ペナルティ)」のバランスを取る指標
です。
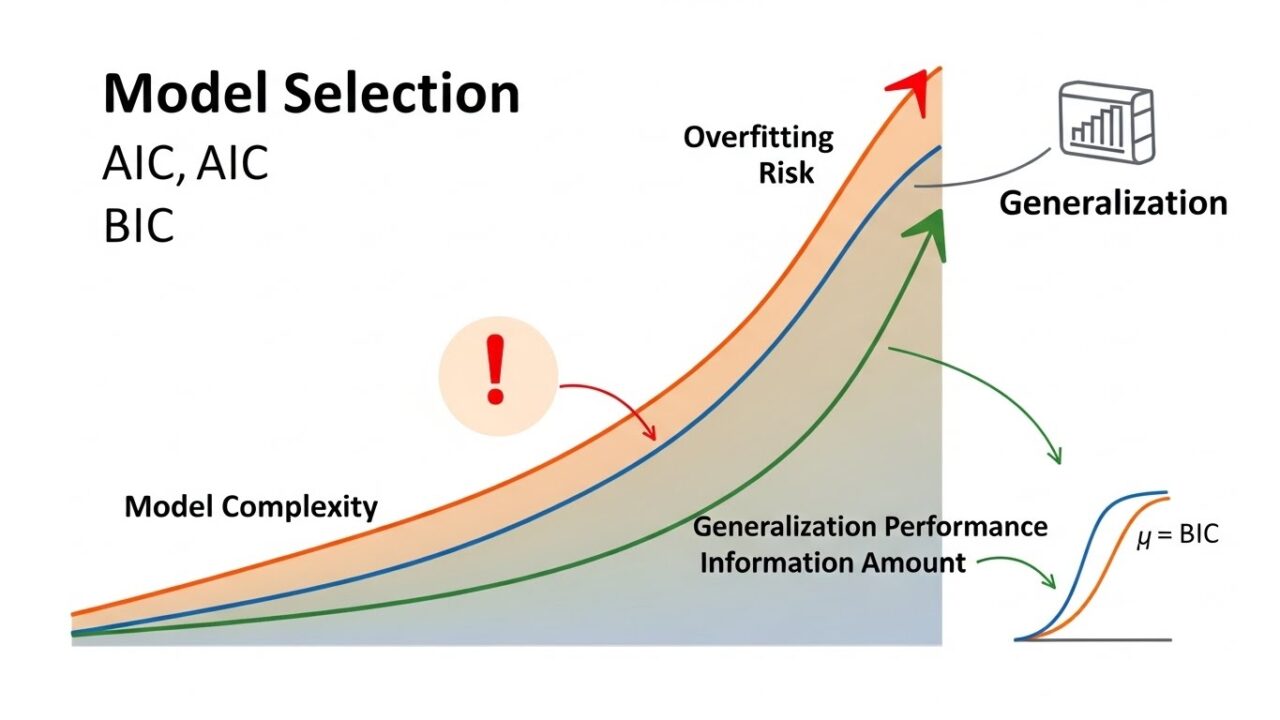
“情報量”として理解する
AIC・BICは、単に「小さい方が良い」という指標ではありません。
本質は、モデルがどれだけ“情報を失っているか”を測る尺度です。
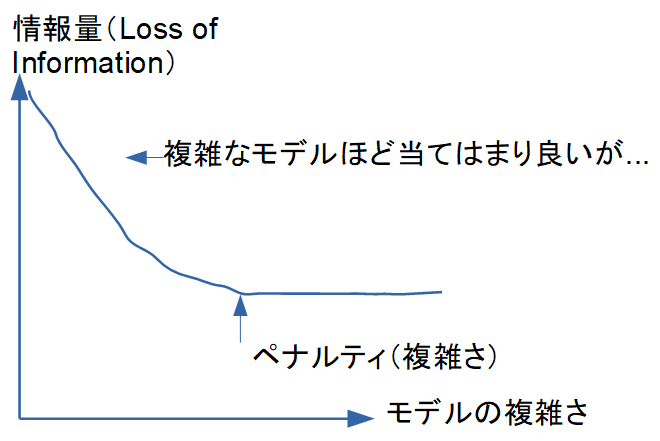
- 左下:単純すぎるモデル → 当てはまりが悪い
- 右上:複雑すぎるモデル → 過学習
- AIC/BICはこの曲線の最小点を探す
AIC/BICは、
「モデルがデータ生成過程からどれだけ離れているか(情報損失)」
を推定し、その最小化を目指します。
過学習と汎化の関係
モデル選択の本質は、未知データでの予測性能(汎化性能)を最大化することです。
過学習とは?
学習データに特化しすぎて、ノイズまで拾ってしまう状態。
複雑モデルは学習データでは高精度でも、未知データでは性能が落ちます。
- 当てはまり(尤度)が良くなるほど -2 log L は小さくなる
- しかし複雑さ(k)が増えるとペナルティが増える
つまり、
「複雑にしすぎるとペナルティが重くなる」
という仕組みで過学習を抑制します。
AICとBICの違い
AICとBICの違いは、ペナルティの強さです。
\[\mathrm{AICのペナルティ}=2k\]
\[\mathrm{BICのペナルティ}=k\log n\]
サンプルサイズ \(n\) が大きいほど、
\(\log n\) は増えるため、BICはより強く複雑さを罰する傾向があります。
要約しますと、以下のように区別することができます。
- AIC:複雑なモデルを許容しやすい
- BIC:より単純なモデルを選びやすい
実務でどちらを使うべきか?
ここが最も気になるポイントでしょう。結論から言うと、目的とデータ量で使い分けるのが合理的です。
① 予測性能を重視するなら AIC
AICは「真のモデルが存在しない」ことを前提に、
未知データでの予測誤差を最小化するモデルを選ぶための指標です。
- 機械学習的な文脈
- 実務での予測モデル
- ノイズが多く、真のモデルが複雑な可能性がある場合
こうした場面ではAICが適しています。
② 真のモデルを特定したいなら BIC
BICは「真のモデルが存在する」ことを前提に、
そのモデルを同定することを目的としています。
- 因果推論
- パラメトリックな統計モデル
- サンプルサイズが大きい場合
こうした場面ではBICが有利です。
③ サンプルサイズでの使い分け
- n が小さい → AIC
- n が大きい → BIC
BICのペナルティは \(k\log n\) なので、\(n\) が大きいほど強く効きます。
そのため、大規模データではBICがより単純なモデルを選びやすくなります。
AIC/BICの実務的な注意点
- 候補モデルの“外側”は評価できない
AIC/BICは、比較対象の中で最良のモデルを選ぶだけです。候補に入っていないモデルは評価できません。 - モデルの誤指定には弱い
とくにBICは「真のモデルが候補に含まれている」ことを前提にしています。 - 尤度が計算できるモデルに限定される
一般的な機械学習モデル(ランダムフォレストなど)では使えません。
まとめ
AICとBICは、モデルの当てはまりと複雑さのバランスを評価し、過学習を防ぎつつ汎化性能を高めるための指標である。AICは予測誤差の最小化を目的とし、複雑なモデルも比較的許容する。一方、BICは真のモデルの同定を重視し、サンプルサイズが大きいほど強いペナルティを課すため、より単純なモデルを選びやすい。実務では、予測性能を重視する場合はAIC、因果推論やモデル同定を目的とする場合はBICが適している。サンプルサイズが小さいときはAIC、大きいときはBICを選ぶのが一般的な指針である。AIC/BICは“情報損失”を最小化するための道具として理解すると、より合理的なモデル選択が可能になる。