仮説検定の“二種類の誤り”を深く理解する― α・β・検出力の関係を直感的に掘り下げる

記事の目次

はじめに

統計的仮説検定を学ぶと必ず登場するのが、第I種の誤り（Type I error）と第II種の誤り（Type II error）、そしてそれらと密接に関係する検出力（Power）です。
しかし、多くの入門書では「定義の紹介」にとどまり、なぜそれが重要なのか、どのように直感的に理解すればよいのか、さらにサンプルサイズ設計とどうつながるのかまで踏み込んで説明されることは多くありません。この記事では、図解・数式・直感的理解を軸に、これらの概念を深く理解できるように整理します。

仮説検定の基本構造：二つの世界を見比べる作業

仮説検定は、次の二つの世界を比較する作業です。

帰無仮説 \(H_0\)：効果なし、差なし、変化なし
対立仮説 \(H_1\)：効果あり、差あり、変化あり

例えば、平均値の差の検定なら、

\[H_0:\mu =\mu _0,\quad H_1:\mu \neq \mu _0\]

のように設定します。

検定とは、観測データから得られる統計量（例：t値）が、帰無仮説のもとでどれくらい起こりやすいかを評価し、
「これは帰無仮説では説明できないほど珍しい」
と判断したら \(H_0\) を棄却する、という手続きです。

第I種の誤り・第II種の誤りを図で理解する

二つの誤りの定義

実際の状態	検定の判断	結果
\(H_0\) が真	\(H_0\) を棄却	第I種の誤り（\(\alpha\)）
\(H_1\) が真	\(H_0\) を採択	第II種の誤り（\(\beta\)）

つまり、

α（第I種の誤り）：本当は効果がないのに「ある」と言ってしまう
β（第II種の誤り）：本当は効果があるのに「ない」と言ってしまう

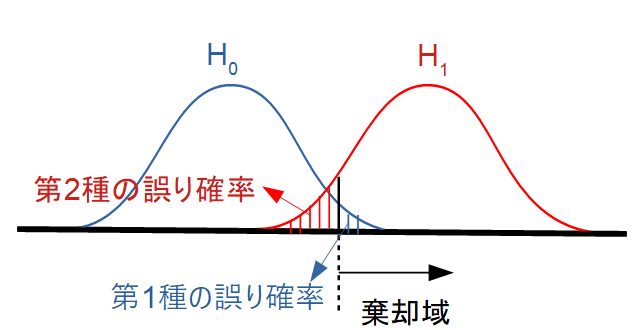
α（第I種の誤り）は「棄却域の面積」
帰無仮説が正しいとき、統計量が棄却域に入ってしまう確率です。
通常は 5%（α=0.05） など、研究者が事前に設定します。
β（第II種の誤り）は「対立仮説のもとで棄却域に入らない確率」
対立仮説が正しいのに、統計量が棄却域に届かず、効果を見逃してしまう確率です。

検出力（Power）とは何か

検出力とは、

\[\mathrm{Power}=1-\beta\]

で定義されます。

つまり、

本当に効果があるときに、それを正しく検出できる確率

です。

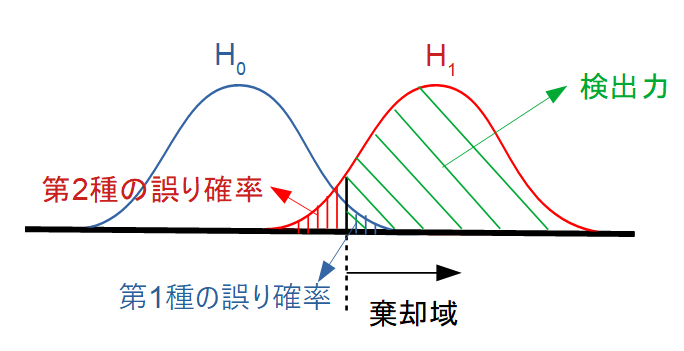
効果量が大きいほど検出力は上がる
差が大きければ、統計量は棄却域に入りやすくなるためです。
サンプルサイズが大きいほど検出力は上がる
標準誤差が小さくなり、分布がシャープになるためです。
αを大きくすると検出力は上がる
棄却域が広がるためですが、誤検出（偽陽性）が増えるため注意が必要です。

数式で見る α・β・検出力の関係

平均の差の検定（片側検定）を例にします。

帰無仮説のもとでの統計量は

\[Z=\frac{\bar {X}-\mu _0}{\sigma /\sqrt{n}}\]

棄却域は

\[Z>z_{1-\alpha }\]

対立仮説のもとでは平均が \(\mu _1\) にずれるため、Zの分布もシフトします。

βは次のように書けます。

\[\beta =\Phi \left( z_{1-\alpha }-\frac{\mu _1-\mu _0}{\sigma /\sqrt{n}}\right)\]

ここで、

効果量：\(\delta =\frac{\mu _1-\mu _0}{\sigma }\)
標準誤差：\(\sigma /\sqrt{n}\)

とすると、検出力は

\[\mathrm{Power}=1-\Phi \left( z_{1-\alpha }-\delta \sqrt{n}\right)\]

この式から、次のことが直感的に読み取れます。

α を大きくすると Power は上がる（ただし誤検出が増える）
n が大きいほど Power は上がる
効果量 δ が大きいほど Power は上がる

サンプルサイズ設計の基礎：検出力から逆算する

実務では、次のような問いが頻繁に登場します。

「効果量 δ を検出するには、どれくらいのサンプルサイズが必要か」

検出力を 80%（0.8）に設定することが多いため、

\[1-\beta =0.8\]

を満たすように n を求めます。

上の式を n について解くと、

\[n=\left( \frac{z_{1-\alpha }+z_{1-\beta }}{\delta }\right) ^2\]

となります。

効果量 δ が小さいほど、必要な n は急激に増える
α を厳しく（小さく）すると、必要な n は増える
β を厳しく（検出力を高く）すると、必要な n は増える

つまり、「誤りを減らす」ことと「サンプルサイズ」にはトレードオフがあるということです。

二種類の誤りのバランスをどう考えるか

研究や実務では、次のような判断が求められます。

第I種の誤り（偽陽性）をどれだけ許容するか
第II種の誤り（偽陰性）をどれだけ許容するか

例えば、

医療の副作用検出 → 偽陰性（見逃し）が致命的
新商品の効果検証 → 偽陽性（誤検出）がコスト増につながる
A/Bテスト → 偽陽性・偽陰性の両方がビジネス判断に影響

このように、どちらの誤りがより重大かは文脈によって異なります。

まとめ

仮説検定における 第I種の誤り（α）・第II種の誤り（β）・検出力（Power） は、単なる定義の暗記ではなく、統計的判断の根幹を形づくる概念です。これらを理解することで、検定という手続きが「二つの世界（H₀ と H₁）の分布を比較し、どちらがデータをより説明するかを判断する作業」であることが立体的に見えてきます。
第I種の誤りは「効果がないのにあると言ってしまう」誤検出であり、研究の信頼性に直結します。一方、第II種の誤りは「効果があるのに見逃してしまう」誤判定で、実務では重大な意思決定ミスにつながることもあります。検出力はこの第II種の誤りを補う指標であり、「本当に効果があるときに、それを正しく検出できる確率」として、実験計画やA/Bテストの成功に欠かせません。
さらに、効果量・サンプルサイズ・αの設定が検出力を決めるという関係式から、サンプルサイズ設計が「誤りのバランスをどう取るか」という意思決定そのものであることが理解できます。効果量が小さいほど大きなサンプルが必要になり、αやβを厳しくするほど必要なデータ量は増えます。つまり、統計的判断は常に「どの誤りをどれだけ許容するか」というトレードオフの上に成り立っています。