データ可視化の中級:箱ひげ図・バイオリンプロット・散布図行列の読み方
記事の目次
Toggleはじめに
分布を「形」として読む力は、実務の分析精度を一段引き上げてくれます。
ここでは、箱ひげ図・バイオリンプロット・散布図行列を題材に、何を強調するグラフなのか、分布の形をどう読むか、実務での誤解されやすいポイント、Rでの実装コードをまとめて解説します。
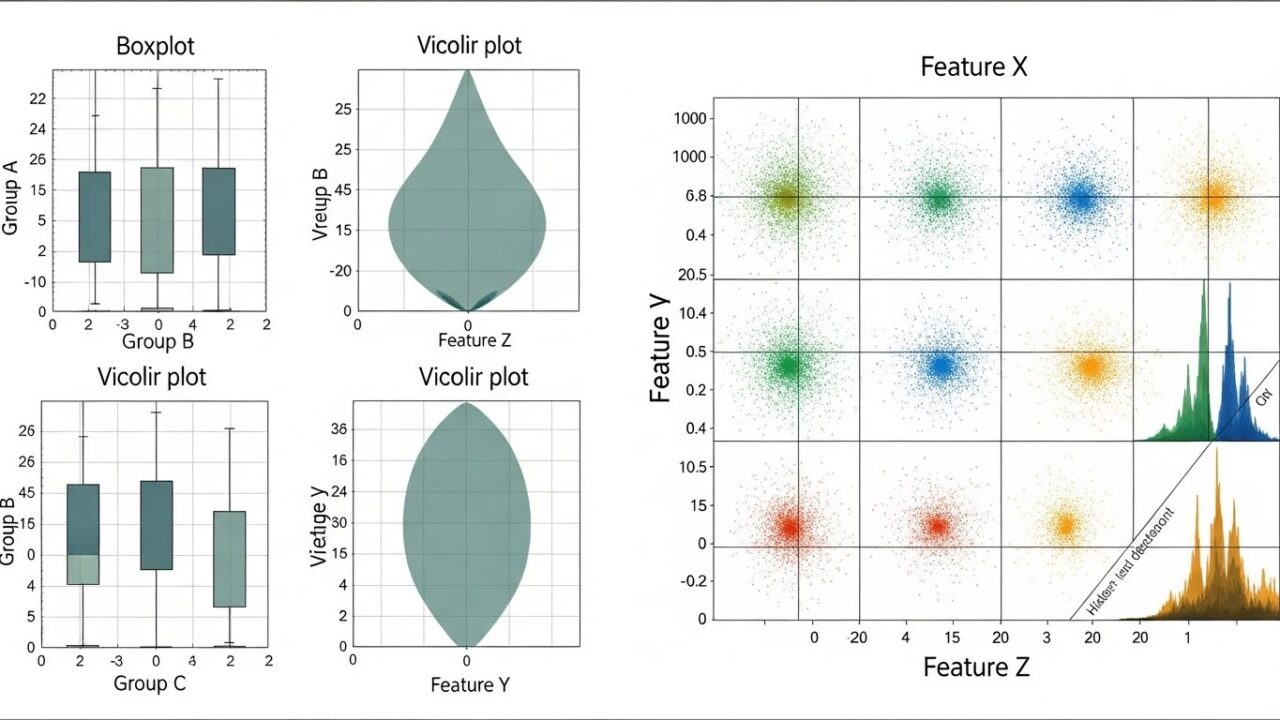
箱ひげ図:分布の要約と外れ値を一目でつかむ
箱ひげ図は、以下の5つの代表値で分布を要約します。
- 最小値
- 第1四分位(Q1)
- 中央値(Q2)
- 第3四分位(Q3)
- 最大値
- + 外れ値(しばしば点で表示)
何を強調するグラフか
- 中央値:分布の中心
- IQR(Q1〜Q3):ばらつきの大きさ
- ひげ:全体の広がり
- 外れ値:異常値・重要なシグナル候補
分布の形の読み方
- 中央値が箱の上寄り → 下側にデータが多い(左寄り)
- 上ひげが長い → 大きい値側に広がり
- 外れ値が多い → ばらつきが大きい or 異常値混在
実務での誤解例
- 中央値が高い=平均も高い
→ 外れ値が大きいと平均は簡単に引っ張られる。 - ひげが長い=データが多い
→ ひげは「範囲」であり「密度」ではない。
#データ準備
data(iris)
# 種ごとに Sepal.Length の箱ひげ図
boxplot(Sepal.Length ~ Species,
data = iris,
main = “Sepal Length by Species”,
xlab = “Species”,
ylab = “Sepal Length”,
col = c(“skyblue”, “lightgreen”, “salmon”))
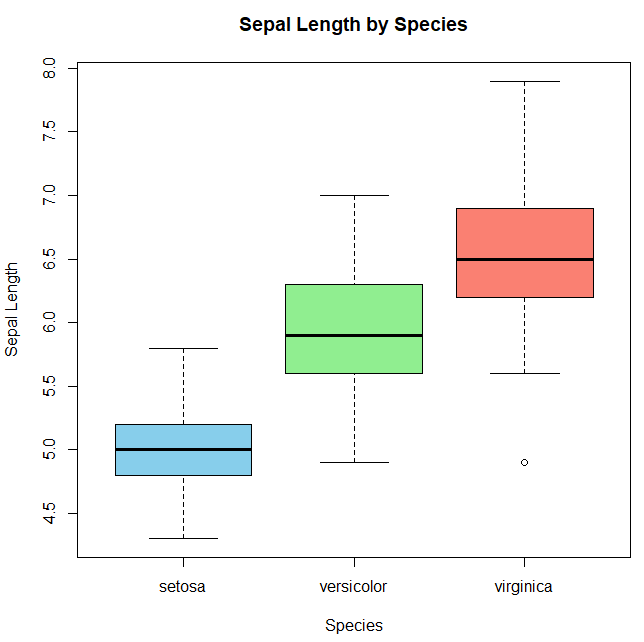
バイオリンプロット:分布の形と密度を可視化する
バイオリンプロットは、箱ひげ図に カーネル密度推定(KDE) を重ねたものです。
「どの値のあたりにどれくらいデータが集中しているか」を直感的に把握できます。
何を強調するグラフか
- 分布の形(山の数・尖り・広がり)
- 密度の高さ(太さ)
- 箱ひげ図の情報(中央値・IQR)も併記可能
分布の形の読み方
- 太い部分 → その値付近にデータが集中
- 細い部分 → データが少ない
- 複数の膨らみ → 多峰性(複数グループ混在)
- 左右非対称 → 分布の偏り
実務での誤解例
- 太い=データ数が多い
→ 正しくは「その値付近の密度が高い」だけ。 - 多峰性=異常
→ 実は「異なるグループが混ざっているだけ」のことも多い。
#パッケージ読み込み
library(ggplot2)
#種ごとの Sepal.Length のバイオリンプロット
ggplot(iris, aes(x = Species, y = Sepal.Length, fill = Species)) +
geom_violin(trim = FALSE, alpha = 0.6) +
geom_boxplot(width = 0.15, outlier.size = 1.5, alpha = 0.8) +
labs(title = “Violin Plot of Sepal Length by Species”,
x = “Species”,
y = “Sepal Length”) +
theme_minimal()
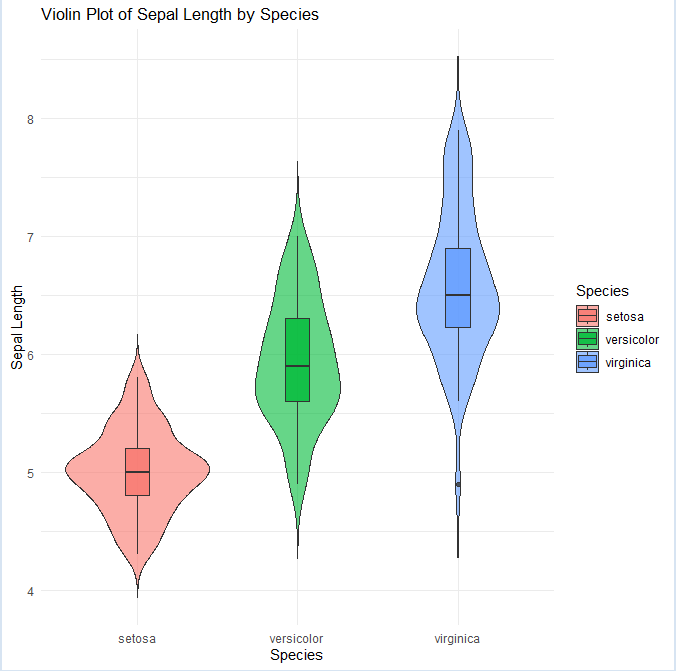
散布図行列:変数同士の関係を一気に俯瞰する
散布図行列(pairplot)は、複数の変数の組み合わせをすべて散布図として並べたものです。
対角線上には各変数の分布(ヒストグラムなど)が表示されることが多いです。
何を強調するグラフか
- 変数間の相関(線形・非線形)
- 外れ値の位置
- 分布の偏り(対角線上のヒストグラム)
分布の形の読み方
- 楕円形 → 線形相関が強い
- 扇形 → 分散が増加(ヘテロスケダスティシティ)
- 縦に細い → Xのばらつきが小さい
- 横に細い → Yのばらつきが小さい
実務での誤解例
- 相関がある=因果関係がある
→ 散布図はあくまで「関係性の候補」を示すだけ。 - 外れ値はノイズだから除去すべき
→ 優良顧客・異常な売上・特定施策の影響など、ビジネス上重要なケースも多い。
base R
# 数値列だけを抽出
iris_num <- iris[, 1:4]
# 散布図行列
pairs(iris_num,
main = “Scatterplot Matrix of Iris Numeric Variables”,
pch = 19,
col = as.numeric(iris$Species))
GGally
# パッケージ読み込み
library(GGally)
# 種も色分けに含めた散布図行列
ggpairs(iris,
columns = 1:4,
aes(color = Species, alpha = 0.7)) +
theme_minimal()
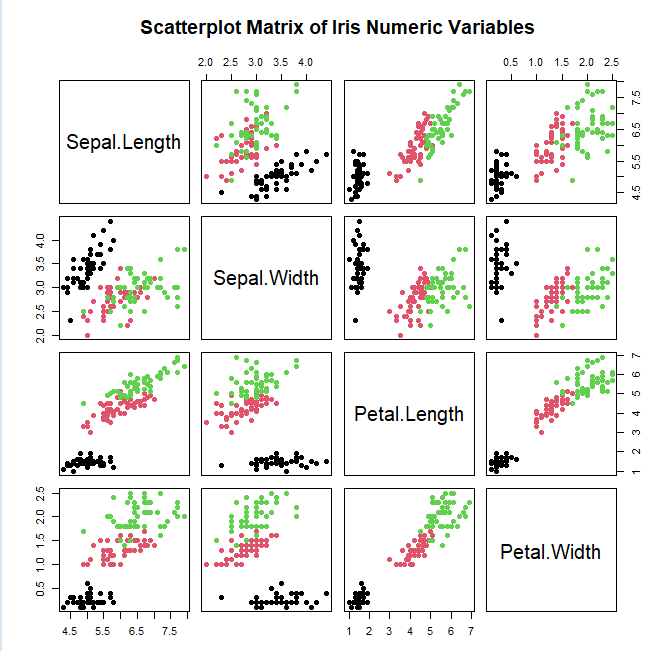
実務で誤解されやすい可視化パターンまとめ
| 可視化 | よくある誤解 | 正しい理解 |
| 箱ひげ図 | 中央値が高い=平均も高い | 外れ値で平均は大きく変動する |
| 箱ひげ図 | ひげが長い=データが多い | ひげは範囲であり、密度や件数は表さない |
| バイオリン | 太い=データ数が多い | その値付近の密度が高いだけ |
| バイオリン | 多峰性=異常 | 異なるグループが混在している可能性が高い |
| 散布図行列 | 相関がある=因果関係がある | 因果は別途設計・検証が必要 |
| 全般 | 外れ値=ノイズなので除去すべき | ビジネス上の重要なシグナルであることも多い |
まとめ
データ可視化を正しく読み解く力は、分析の質を大きく左右します。箱ひげ図は分布の要約と外れ値の把握に優れ、バイオリンプロットは分布の形や密度を直感的に理解する助けになります。さらに散布図行列を使えば、複数の変数同士の関係性を一度に俯瞰できます。これらの可視化はそれぞれ強調するポイントが異なり、読み取り方を誤ると意思決定に影響を与える可能性もあります。
特に実務では、中央値と平均値の混同、密度とデータ数の取り違え、相関と因果の誤解、外れ値の早期除外など、誤読につながる落とし穴が少なくありません。だからこそ、グラフの形が何を意味し、どのような背景を示唆しているのかを丁寧に読み解く姿勢が求められます。
Rで実際に可視化を描きながら確認することで、分布の特徴や変数間の関係がより鮮明に理解できます。可視化は単なる“図”ではなく、データのストーリーを読み解くための強力なツールです。今回紹介した3つの可視化を使いこなすことで、データの本質により深く迫ることができるはずです。