母相関係数の検定と信頼区間、二つの母相関係数の検定をやさしく解説
記事の目次
Toggleはじめに
相関係数は「2つの変数の関係」を測る、とても身近で重要な指標です。
しかし、
- 「相関係数が 0.4 って、統計的に有意なの?」
- 「相関係数の信頼区間ってどうやって求めるの?」
- 「2つのグループで相関が違うかどうか比べたい」
といったところで、急にハードルが上がったように感じる方も多いと思います。この記事では、母相関係数の検定と信頼区間、二つの母相関係数の検定を丁寧に解説します。
相関係数とは?直感と図でおさらい
まずは相関係数の直感から確認します。
2つの変数 X,Y のピアソンの相関係数 r は次の式で定義されます。
\[r=\frac{\sum _{i=1}^n(x_i-\bar {x})(y_i-\bar {y})}{\sqrt{\sum _{i=1}^n(x_i-\bar {x})^2}\sqrt{\sum _{i=1}^n(y_i-\bar {y})^2}}\]
- \(-1\leq r\leq 1\)の範囲をとります。
- r>0:片方が大きいほどもう片方も大きくなる(正の相関)
- r<0:片方が大きいほどもう片方は小さくなる(負の相関)
- \(r\approx 0\):直線的な関係は弱い
set.seed(123)
# 強い正の相関
n <- 50
x <- rnorm(n, mean = 0, sd = 1)
y <- 0.8 * x + rnorm(n, sd = 0.5)
cor(x, y)
plot(x, y,
main = paste0(“散布図(r = “, round(cor(x, y), 2), “)”),
xlab = “X”, ylab = “Y”,
pch = 19, col = “steelblue”)
abline(lm(y ~ x), col = “red”, lwd = 2)
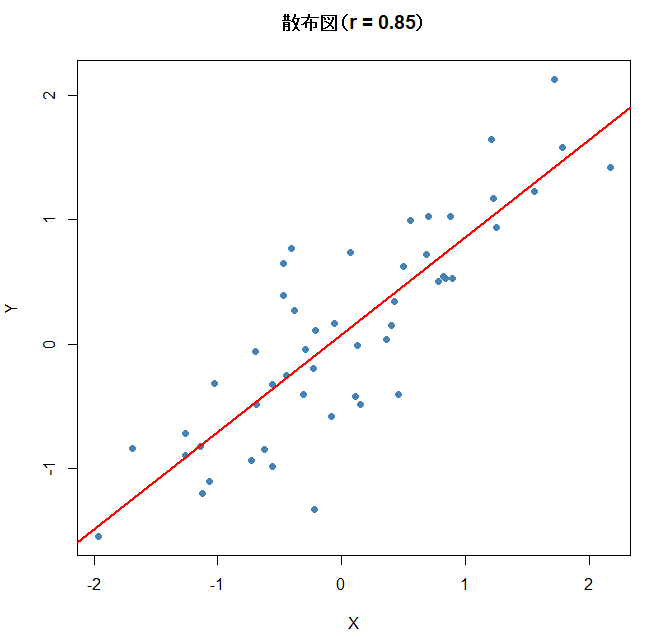
視覚的に「点がどれくらい一直線に並んでいるか」を見ると、相関のイメージがつかみやすくなります。
母相関係数の検定(\(\rho =0\) かどうか)
次に、「サンプル相関係数 r が得られたとき、それが偶然なのか、本当に母集団で相関があるのか」を検定します。
仮説の立て方
- 帰無仮説:\(H_0:\rho = 0\quad\) (母相関係数は0である)
- 対立仮説 : \(H_1:\rho \neq 0\quad\) (母相関係数は0ではない)
検定統計量(t検定)
サンプルサイズを n、サンプル相関係数を r とすると、次の統計量を使います。
\[t=\frac{r\sqrt{n-2}}{\sqrt{1-r^2}}\]
この t は、自由度 n-2 の t 分布に従います(帰無仮説が正しいとき)。
- |t| が大きいほど、\(\rho =0\) から離れている
- t 分布の両側の確率を使って p 値を計算
具体例
例として、
- n=20
- r=0.45
とします。
\[t=\frac{0.45\sqrt{20-2}}{\sqrt{1-0.45^2}}=\frac{0.45\sqrt{18}}{\sqrt{1-0.2025}}\approx \frac{0.45\times 4.243}{\sqrt{0.7975}}\approx \frac{1.909}{0.893}\approx 2.14\]
自由度18の t 分布で |t|=2.14 の両側確率を求めると、
p 値はだいたい 0.04 程度になり、5%有意水準で有意と判断できます。
Rで相関の検定を行う
set.seed(123)
n <- 20
x <- rnorm(n)
y <- 0.5 * x + rnorm(n)
# 相関係数
cor(x, y)
# 相関の検定
res <- cor.test(x, y, method = “pearson”)
res
Pearson’s product-moment correlation
data: x and y
t = 2.3, df = 18, p-value = 0.033
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.05 0.75
sample estimates:
cor
0.47
ここから、
- 検定統計量 t
- 自由度
df - p 値
- 相関係数の95%信頼区間
が一度に確認できます。
母相関係数の信頼区間:Fisherの z 変換
相関係数 r は、値の範囲が [-1,1] に制限されているため、そのままでは分布が歪んでしまいます。
そこで、Fisher の z 変換を使って、ほぼ正規分布に従う量に変換します。
Fisher の z 変換
サンプル相関係数 r に対して、
\[z=\frac{1}{2}\ln \left( \frac{1+r}{1-r}\right)\]
と変換します。
この z は、サンプルサイズが十分大きいとき、近似的に
\[z\sim N\left( \zeta ,\frac{1}{n-3}\right)\]
に従います。ここで \(\zeta\) は真の母相関係数 \(\rho\) に対応する z 変換です。
z の標準誤差
\[SE_z=\frac{1}{\sqrt{n-3}}\]
z の信頼区間(95%)
95%信頼区間は、
\[z_{\mathrm{lower}}=z-1.96\cdot SE_z\]
\[z_{\mathrm{upper}}=z+1.96\cdot SE_z\]
と求められます。
z から相関係数への逆変換
求めた区間を、相関係数のスケールに戻します。
\[\rho =\frac{e^{2z}-1}{e^{2z}+1}\]
したがって、
\[\rho _{\mathrm{lower}}=\frac{e^{2z_{\mathrm{lower}}}-1}{e^{2z_{\mathrm{lower}}}+1},\quad \rho _{\mathrm{upper}}=\frac{e^{2z_{\mathrm{upper}}}-1}{e^{2z_{\mathrm{upper}}}+1}\]
となります。
具体例
例として、
- n=30
- r=0.40
とします。
z 変換
\[z=\frac{1}{2}\ln \left( \frac{1+0.4}{1-0.4}\right) =\frac{1}{2}\ln \left( \frac{1.4}{0.6}\right) =\frac{1}{2}\ln (2.333…)\approx \frac{1}{2}\times 0.847\approx 0.424\]
標準誤差
\[SE_z=\frac{1}{\sqrt{30-3}}=\frac{1}{\sqrt{27}}\approx 0.192\]
z の95%信頼区間
\[z_{\mathrm{lower}}=0.424-1.96\times 0.192\approx 0.424-0.376\approx 0.048\]
\[z_{\mathrm{upper}}=0.424+1.96\times 0.192\approx 0.424+0.376\approx 0.800\]
相関係数に戻す
\[\rho _{\mathrm{lower}}=\frac{e^{2\times 0.048}-1}{e^{2\times 0.048}+1}=\frac{e^{0.096}-1}{e^{0.096}+1}\approx \frac{1.101-1}{1.101+1}\approx \frac{0.101}{2.101}\approx 0.048\]
\[\rho _{\mathrm{upper}}=\frac{e^{2\times 0.800}-1}{e^{2\times 0.800}+1}=\frac{e^{1.6}-1}{e^{1.6}+1}\approx \frac{4.953-1}{4.953+1}\approx \frac{3.953}{5.953}\approx 0.664\]
したがって、
母相関係数の95%信頼区間はおよそ [0.05,0.66] となります。
RでFisherの z を使って信頼区間を計算する
fisher_ci <- function(r, n, conf.level = 0.95) {
z <- 0.5 * log((1 + r) / (1 – r))
se <- 1 / sqrt(n – 3)
alpha <- 1 – conf.level
z_crit <- qnorm(1 – alpha / 2)
z_lower <- z – z_crit * se
z_upper <- z + z_crit * se
r_lower <- (exp(2 * z_lower) – 1) / (exp(2 * z_lower) + 1)
r_upper <- (exp(2 * z_upper) – 1) / (exp(2 * z_upper) + 1)
c(lower = r_lower, upper = r_upper)
}
set.seed(123)
n <- 30
x <- rnorm(n)
y <- 0.4 * x + rnorm(n)
r <- cor(x, y)
r
fisher_ci(r, n)
これで、cor.test() の結果と見比べると、「こうやって信頼区間が計算されているのか」と腑に落ちやすくなります。
二つの母相関係数の検定(独立な2群)
次に、「2つのグループで相関が違うかどうか」を検定します。
例:
- 男性の「身長と体重」の相関
- 女性の「身長と体重」の相関
これらが同じかどうかを調べたい、という状況です。
独立な2群の相関係数の比較
2つのグループが独立であるとします。
- グループ1:相関係数 r_1、サンプルサイズ n_1
- グループ2:相関係数 r_2、サンプルサイズ n_2
まず、それぞれを Fisher の z に変換します。
\[z_1=\frac{1}{2}\ln \left( \frac{1+r_1}{1-r_1}\right) ,\quad z_2=\frac{1}{2}\ln \left( \frac{1+r_2}{1-r_2}\right)\]
検定統計量
2つの z の差を、標準誤差で割ったものを検定統計量とします。
\[Z=\frac{z_1-z_2}{\sqrt{\frac{1}{n_1-3}+\frac{1}{n_2-3}}}\]
この Z は、近似的に標準正規分布 N(0,1) に従うとみなせます。
- |Z| が大きいほど、2つの相関が異なる可能性が高い
- p 値は標準正規分布から計算
具体例
例として、
- 男性:r_1=0.50,n_1=40
- 女性:r_2=0.20,n_2=35
とします。
z 変換
\[z_1=0.5\ln \left( \frac{1+0.5}{1-0.5}\right) =0.5\ln \left( \frac{1.5}{0.5}\right) =0.5\ln (3)\approx 0.5\times 1.099\approx 0.549\]
\[z_2=0.5\ln \left( \frac{1+0.2}{1-0.2}\right) =0.5\ln \left( \frac{1.2}{0.8}\right) =0.5\ln (1.5)\approx 0.5\times 0.405\approx 0.203\]
標準誤差
\[SE=\sqrt{\frac{1}{n_1-3}+\frac{1}{n_2-3}}=\sqrt{\frac{1}{37}+\frac{1}{32}}\approx \sqrt{0.0270+0.0313}\approx \sqrt{0.0583}\approx 0.241\]
検定統計量
\[Z=\frac{z_1-z_2}{SE}=\frac{0.549-0.203}{0.241}=\frac{0.346}{0.241}\approx 1.44\]
標準正規分布で |Z|=1.44 の両側確率は、p 値としておよそ 0.15 程度です。
したがって、5%有意水準では「相関に有意な差はない」と判断します。
Rで2つの相関係数の差の検定を実装する
compare_cor_independent <- function(r1, n1, r2, n2) {
z1 <- 0.5 * log((1 + r1) / (1 – r1))
z2 <- 0.5 * log((1 + r2) / (1 – r2))
se <- sqrt(1 / (n1 – 3) + 1 / (n2 – 3))
z <- (z1 – z2) / se
p <- 2 * (1 – pnorm(abs(z)))
list(
z_stat = z,
p_value = p
)
}
#例
r1 <- 0.50; n1 <- 40
r2 <- 0.20; n2 <- 35
compare_cor_independent(r1, n1, r2, n2)
この関数を使えば、任意の2群の相関係数の差の検定が簡単にできます。
同一サンプル内での相関係数の比較
少し応用的な話として、同じサンプル内で2つの相関を比較したい場合があります。
例:
- 同じ人たちについて
- X = テストAの点数
- Y = テストBの点数
- Z = テストCの点数
- 「X と Y の相関」と「X と Z の相関」が違うかどうかを知りたい
この場合、2つの相関は同じサンプルから計算されているため独立ではありません。
そのため、先ほどの「独立な2群の比較」の式は使えません。
このようなときには、Steiger の検定など、やや複雑な方法を使います。
実務では、Rの psych パッケージの r.test() 関数などを使うことが多いです
install.packages(“psych”)
library(psych)
# x, y, z が同じサンプルからの3変数とするset.seed(123)
n <- 50
x <- rnorm(n)
y <- 0.6 * x + rnorm(n)
z <- 0.2 * x + rnorm(n)
r_xy <- cor(x, y)
r_xz <- cor(x, z)
r_yz <- cor(y, z)
# Steiger の検定(同一サンプル内の2つの相関の比較)
psych::r.test(n = n, r12 = r_xy, r13 = r_xz, r23 = r_yz)
ここでは詳細な数式展開は省略しますが、
「同じサンプル内での相関の比較は、独立な2群の比較とは別物」
という点だけ押さえておくと、混乱しにくくなります。
まとめ
相関係数はデータ同士の関係を捉える基本的な指標ですが、統計的に正しく扱うためには検定や信頼区間の理解が欠かせません。この記事では、母相関係数が 0 かどうかを調べる t 検定、相関の強さを推定するための Fisher の z 変換による信頼区間、そして二つの相関係数を比較するための検定方法を整理しました。Rコードや図を用いることで、相関の「見える化」から「検定・推定」までの流れを直感的に理解できるように構成しています。相関分析は回帰や因果推論にもつながる重要な基礎であり、今回の内容を押さえることで、より深いデータ解釈へと踏み出す準備が整います。