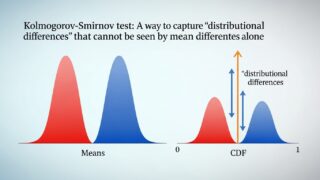
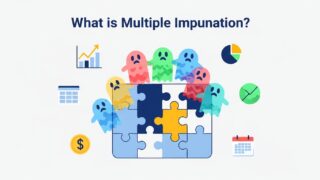
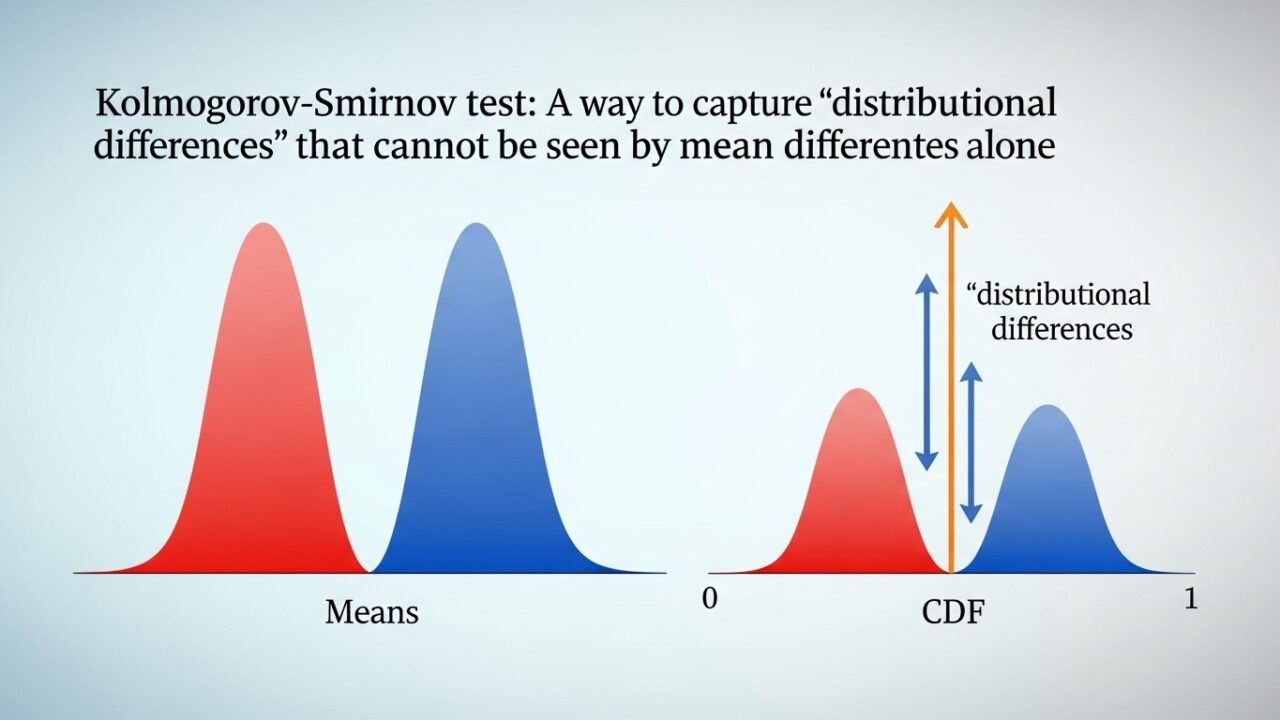
Kolmogorov–Smirnov検定：平均の差だけでは見えない「分布の違い」をとらえる方法

記事の目次

はじめに

2群を比較するとき、多くの人がまず思い浮かべるのは t検定 です。しかし、t検定が評価するのは 平均値の差 に限られます。実務では、平均が同じでも

分布の形が違う
ばらつきが異なる
片側に長い尾がある
二峰性になっている

といったケースが頻繁にあります。こうした「分布全体の違い」を検出したいときに有効なのが Kolmogorov–Smirnov（KS）検定 です。
本記事ではKolmogorov–Smirnov（KS）検定について数式や図解を用いてわかりやすく解説いたします。

KS検定とは何か

KS検定は、2つのサンプルが 同じ分布から来ているかどうか を検定するノンパラメトリック手法です。

比較対象は平均でも分散でもなく、累積分布関数（CDF） です。

KS統計量の定義

2つの経験分布関数を

\[F_n(x),\quad G_m(x)\]

とすると、KS統計量 D は

\[D=\sup _x|F_n(x)-G_m(x)|\]

つまり、2つの経験分布の最大距離 を測ります。

経験分布関数（ECDF）とは？

● 定義

サンプルデータ\(x_1,x_2,\ldots ,x_n\)があるとき、経験分布関数 \(F_n(x)\) は

\[F_n(x)=\frac{\mathrm{サンプルのうち\ }x_i\leq x\mathrm{\ となる個数}}{n}\]

つまり、

ある値 x 以下のデータが全体の何割か
それを 0〜1 の範囲で表した関数

です。

KS検定が有効な場面

平均は同じだが分布が違う
外れ値の多さや歪度の違いを検出したい
分布仮定（正規性など）を置きたくない
製造業・医療・金融などで分布の形状を比較したい

実データを使った応用例

ここでは、実務に近い 製造業の品質管理データ を例にします。

● シナリオ

ある工場で、製品の「直径」を測定しているとします。
ロットAとロットBで平均値はほぼ同じですが、ロットBはばらつきが大きい可能性があります。

実データ例

A <- c(
10.1, 10.0, 10.2, 10.1, 10.0, 10.1, 10.2, 10.1, 10.0, 10.1,
10.2, 10.1, 10.0, 10.1, 10.2, 10.1, 10.0, 10.1, 10.2, 10.1
)

B <- c(
10.1, 9.8, 10.4, 10.0, 10.3, 9.9, 10.5, 10.2, 9.7, 10.4,
10.1, 10.3, 10.6, 9.8, 10.4, 10.2, 9.9, 10.5, 10.3, 9.7
)

それぞれの群の平均値はA：10.10、B：10.12でほぼ同じですが、データを見てみると、Bはばらつきが大きいように見えます。

実データに対するKS検定をR言語で行う際には以下のコードで行うことができます。

KS検定

ks.test(A, B)

出力例

Two-sample Kolmogorov-Smirnov test

D = 0.35, p-value = 0.03
alternative hypothesis: two-sided

解釈：p = 0.03 → 分布が異なると判断

平均値では差が見えなくても、KS検定は分布の違いを検出できます。

また、2つの経験分布関数（ECDF）をR言語で図示してみると以下のようになります。

plot(ecdf(A), col = “blue”, main = “ECDF comparison”,
xlab = “Diameter”, ylab = “ECDF”)
lines(ecdf(B), col = “red”)
legend(“bottomright”, legend = c(“Lot A”, “Lot B”),
col = c(“blue”, “red”), lty = 1)

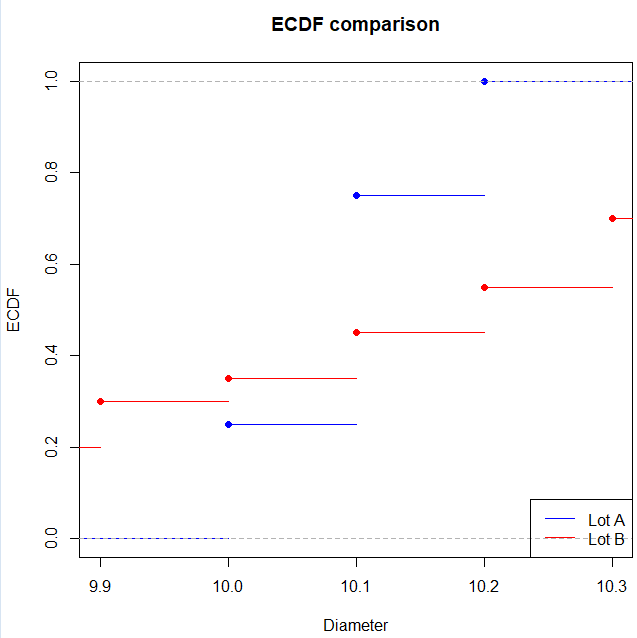
図の読み方

横軸：データ（直径mm）
縦軸：その直径以下の製品が全体の何割か
青線（A）は比較的滑らかでばらつきが小さい
赤線（B）は階段の位置が広く散らばっている
2つの線が最も離れている点が KS 統計量

→ ロットBはばらつきが大きい ことが視覚的にわかる

KS検定の注意点

KS検定の注意点として以下の３点があります。

離散データには厳密には適用できない
→ p値が保守的になる。
サンプルサイズが大きいと些細な差でも有意になる
→ 効果量（D値）も確認する。
どこが違うかまでは教えてくれない
→ 平均・分散・歪度などのどれが原因かは別途調べる必要がある。

実務での利用例

● 医療データ

治療前後で血中濃度の分布が変化したかを確認。

● 製造業

ロット間で寸法分布が変化していないかをチェック。
→ 平均が同じでも、ばらつきが増えていればKS検定で検出可能。

● 金融データ

リターン分布の形状比較（尾の重さ、歪度など）。
→ リスク管理に有用。

まとめ

Kolmogorov–Smirnov（KS）検定は、平均値の差だけでは捉えきれない 分布全体の違い を検出できる、非常に強力なノンパラメトリック手法です。比較の対象となるのは平均や分散ではなく、サンプルから得られる 経験分布関数（ECDF） であり、2つのECDFの最大の隔たり（KS統計量）を用いて分布の差を評価します。分布の形状が異なる場合や、外れ値・歪度・ばらつきの違いを調べたい場合、あるいは正規性などの分布仮定を置きたくない場面で特に有効です。
Rでは ks.test() を使うだけで簡単に実行でき、医療データ、製造業の品質管理、金融データのリスク分析など、実務の幅広い領域で活用されています。平均値だけに注目していると見落としてしまう重要な違いも、KS検定ならしっかりと捉えることができます。分布比較の第一歩として、ぜひ積極的に利用したい手法です。

参考書籍

臨床試験のデザインと解析

[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]

臨床試験のデザインと解析
価格：4,256円（税込、送料別) (2026/2/1時点)

楽天で購入

Kolmogorov–Smirnov検定経験分布関数