比較データに基づくアダプティブデザインと特別な考慮事項:実務で使いこなすための徹底解説

記事の目次
Toggleはじめに
アダプティブデザインは、臨床試験の柔軟性と効率性を高める強力なアプローチです。
特に 比較データ(治療群間の差)を用いたアダプテーション は、試験の成功確率を高める一方で、第一種過誤の増大や推定バイアスといった統計的リスクも伴います。
本記事では、FDA ガイダンスの内容を踏まえながら、比較データに基づくアダプティブデザインと特別な考慮事項 を、実務者向けにわかりやすく整理します。
比較データに基づくアダプティブデザインとは
比較データを用いるアダプテーションは、治療効果の中間推定値を利用して試験を変更する方法です。
FDA ガイダンスでは次のように述べられています:
「比較データに基づくアダプテーションは、第一種の過誤確率が直接増大し、治療効果の推定にバイアスが生じる」
(“比較データに基づくアダプテーションにより、しばしば第一種の過誤確率が直接増大し…”)
つまり、強力だが慎重な設計が必要なデザインです。
群逐次デザイン:最も代表的な比較アダプティブデザイン
■ 群逐次デザインの基本構造
群逐次デザインでは、以下のように複数回の中間解析を行い、有効性・無益性の判断に応じて試験を早期終了できます。
■ 第一種過誤を制御するための境界
中間解析を複数回行うと、単純に p<0.025 を繰り返すだけでは第一種過誤が増大します。
そのため、O’Brien–Fleming や Pocock の境界が用いられます。
● O’Brien–Fleming の例
初期の中間解析では非常に厳しい基準を設定し、後半で緩和します。
\[\mathrm{境界例:\ }Z_1=3.5,\; Z_2=2.5,\; Z_{\mathrm{final}}=2.0\]
● Pocock の例
すべての解析でほぼ一定の基準を用います。
\[Z_1=Z_2=Z_{\mathrm{final}}\approx 2.4\]
ガイダンスでも、これらの境界の違いが明確に説明されています:
「O’Brien-Fleming のアプローチでは早期中止には非常に強いエビデンスが必要となる」
症例数再推定(Sample Size Re-estimation)
症例数再推定は、比較データを用いる場合と用いない場合があります。
■ 比較データを用いる SSR(非盲検 SSR)
中間解析で治療効果の推定値を用いて症例数を増減させる方法です。
しかし、ガイダンスは次のように警告します:
「適切な調整を行わずに症例数を変更すると第一種の過誤確率が2倍以上になりうる」
(Proschan & Hunsberger 1995 の引用)
● なぜ過誤が増えるのか?
治療効果の中間推定値 \(\hat {\delta }_{\mathrm{interim}}\) を用いて症例数を増やすと、「効果が大きく見えたときだけ症例数を増やす」という 選択バイアス が生じるためです。
● 対応策:p値の併合法
代表的な方法:
- Bauer & Köhne (1994)
- Cui, Hung & Wang (1999)
- Müller & Schäfer (2001)
これらは、ステージ1とステージ2の p値を統合し、第一種過誤を厳密に制御します。
アダプティブ・エンリッチメント(患者集団の変更)
治療効果が特定のサブグループで大きいと予想される場合、中間解析で 対象集団を変更 するデザインです。
例:
- 全体集団で効果が弱い
- しかしバイオマーカー陽性群では効果が強い
→ 中間解析後は陽性群のみを登録する
ガイダンスでは次のように述べられています:
「アダプティブ・エンリッチメントでは、複数集団の仮説検定に伴う多重性を考慮する必要がある」
● 多重性の例
- 全体集団の仮説:\(H_0^{\mathrm{all}}\)
- サブ集団の仮説:\(H_0^{\mathrm{sub}}\)
これらを同時に扱うため、閉手続き法 や 重み付き Bonferroni が用いられます。
治療群選択(アダプティブアームドロップ)
複数用量・複数治療を比較する試験で、中間解析に基づき 効果の弱い群を除外 する方法です。
例:
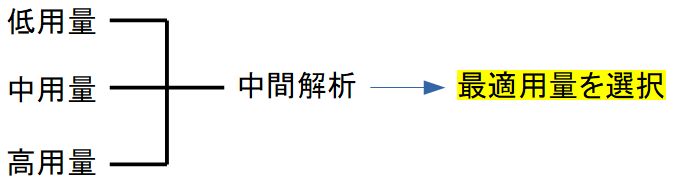
ガイダンスでは、用量選択の際の注意点として:
「多重性と症例数変更の両方を考慮した仮説検定手法が必要」
反応に基づくアダプティブランダム化(RAR)
患者の割付比を、蓄積されたアウトカムに応じて変更する方法です。
例:
- 有望な治療群により多くの患者を割り付ける
- 倫理的メリットがある
しかし、ガイダンスは次のように注意を促します:
「反応に基づくアダプティブランダム化には議論があり、2群試験では効率改善が限定的」
評価項目のアダプテーション
主要評価項目を中間解析で変更するデザインです。
例:
- 主要評価項目を「症状改善」→「入院回避」に変更
ガイダンスは明確に述べています:
「評価項目の変更には重要な臨床的考慮が含まれるため、FDA と早期に協議すべき」
特別な考慮事項
■8.1 シミュレーションは必須
複雑なアダプティブデザインでは、解析的に第一種過誤を導出できないケースが多くあります。
ガイダンスでは:
「アダプティブデザインでは動作特性の評価にシミュレーションが特に重要」
● シミュレーションで評価すべき項目
- 第一種過誤
- 検出力
- 期待症例数
- 最大症例数
- 推定値のバイアス
- 信頼区間の被覆率
● シナリオ設定の例
\[\mathrm{治療効果\ }\delta \in \{ 0,0.2,0.4,0.6\}\]
\[\mathrm{対照群イベント率\ }p\in \{ 0.2,0.4,0.6\}\]
■ 8.2 ベイズ流アダプティブデザイン
ベイズ流では、事後確率を用いて意思決定を行います。
例:
\[P(\delta >0\mid \mathrm{data})>0.99\Rightarrow \mathrm{有効性で中止}\]
ガイダンスでは:
「ベイズ流デザインでも動作特性の評価にはシミュレーションが不可欠」
■ 8.3 イベント発現までの時間を扱う場合
TTE(Time-to-event)試験では、イベント数が検出力を決めるため、症例数だけでなく 追跡期間の調整 が必要です。
■ 8.4 中間評価項目・代替評価項目の利用
主要評価項目が遅くしか得られない場合、中間評価項目を用いてアダプテーションを行うことがあります。
しかし:
「代替評価項目の誤指定は第一種過誤の増大につながる」
まとめ
比較データに基づくアダプティブデザインは、治療群間の差を利用して試験を柔軟に変更する手法であり、群逐次デザイン、症例数再推定、アダプティブ・エンリッチメント、治療群選択、アダプティブランダム化などが含まれます。これらは試験の効率性や倫理性を高める一方、第一種過誤の増大や推定バイアスといった統計的リスクを伴うため、厳密な事前計画と適切な解析手法が不可欠です。
群逐次デザインでは、中間解析で有効性・無益性を判断し早期終了が可能ですが、O’Brien–Fleming や Pocock のような境界設定により第一種過誤を制御する必要があります。症例数再推定では、比較データを用いる場合に過誤が増大しやすく、p値の併合法などの調整手法が求められます。アダプティブ・エンリッチメントでは、サブグループへの集団変更に伴う多重性の管理が重要となり、治療群選択では用量選択と多重性の両方を考慮した設計が必要です。アダプティブランダム化は倫理的利点があるものの、2群試験では効率改善が限定的とされています。
特別な考慮事項として、複雑なアダプティブデザインではシミュレーションが必須であり、第一種過誤、検出力、期待症例数、推定バイアスなどを多様なシナリオで評価する必要があります。ベイズ流デザインでは事後確率に基づく意思決定が可能ですが、同様に動作特性のシミュレーションが不可欠です。また、イベント発現までの時間を扱う試験では追跡期間の調整が重要となり、中間評価項目や代替評価項目を用いる場合は誤指定による過誤増大に注意が必要です。
総じて、比較データに基づくアダプティブデザインは強力な手法である一方、統計的・運営的な複雑性が高く、事前規定・シミュレーション・試験完全性の維持が成功の鍵となります。
参考資料
アダプティブデザインに関するFDAガイダンスの邦訳(データサイエンス部会 2021年)
https://www.jpma.or.jp/information/evaluation/results/allotment/adaptive_design.html