はじめに:なぜMMRMが注目されるのか
臨床試験では、被験者から複数の時点でデータを収集することが一般的です。たとえば、薬剤の効果を「投与前」「投与後1週」「4週」「8週」などで測定する場合、単純な分散分析(ANOVA)では欠測値や時系列の相関構造に対応できません。
そこで登場するのが MMRM(Mixed Model for Repeated Measures)です。この手法は、欠測値に強く、時系列の相関構造をモデル化できるため、近年の臨床試験では標準的な解析法として広く用いられています。
本記事ではMMRMについて解説していきます。
MMRMの数理的構造
\[Y_{ij} = \mu + \alpha_i + \beta_j + (\alpha\beta)_{ij} + \varepsilon_{ij} \]
- \(Y_{ij}\):被験者 i の時点 j における測定値
- \(\mu\):全体平均
- \(\alpha_i\):群(例:治療群 vs. プラセボ群)の固定効果
- \(\alpha\beta_{ij}\):群×時点の交互作用
- \(\varepsilon_{ij}\):誤差項(共分散構造を持つ)
誤差項 \(\varepsilon_{ij}\) には、非構造型(unstructured)やAR(1) などの共分散構造を指定することで、時系列の相関を柔軟に表現できます。
下記はMMRMでよく使われる共分散構造のイメージ図です。各構造がどのように時点間の相関をモデル化するかを視覚的に示しています。UNは不規則、CSは均一、AR(1)は時間差に応じて減衰するパターンが見て取れます
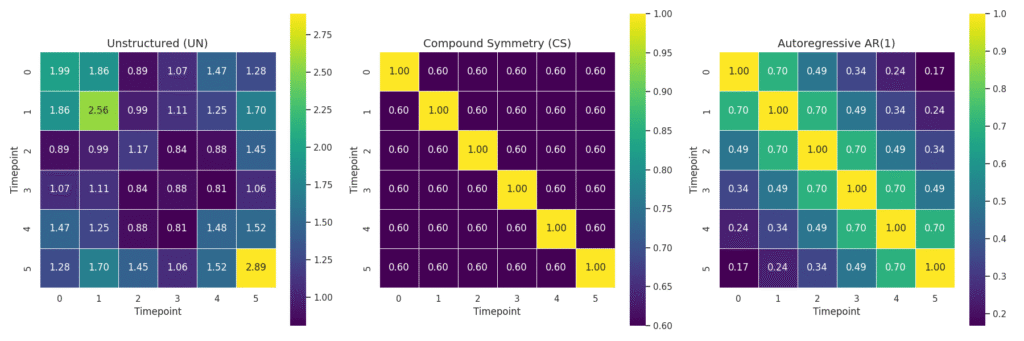
| 構造 | 特徴 | 実務での使い方 |
| Unstructured (UN) | 各時点間の相関が自由に推定される。最も柔軟だがパラメータ数が多い。 | 時点数が少ない場合や、相関構造が複雑な場合に使用 |
| Compound Symmetry (CS) | すべての時点間で同じ相関を仮定。構造が単純で解釈しやすい。 | 時系列の相関が均一と仮定できる場合に適用 |
| Autoregressive AR(1) | 時点間の相関が時間差に応じて指数的に減衰。 | 時系列的な構造がある場合に自然な選択肢 |
MMRMの特徴と利点
MMRMの特徴と利点についてまとめていきます。
| 特徴 | 内容 |
| 欠測値に強い | MAR(Missing at random)を仮定することで、欠測値を除外せずに解析可能 |
| 柔軟な共分散構造 | 時系列の相関をモデル化できるため、精度の高い推定が可能 |
| 群×時点の交互作用を評価可能 | 治療効果の時間的変化を明示的に捉えられる |
| 最小二乗平均(LS Mean)による比較 | 各時点での群間差を推定しやすい |
具体例:抗うつ薬の臨床試験
試験設計:治療群とプラセボ群にランダム化し、うつ症状スコア(例:HAM-D)を0週、2週、4週、8週で測定。
目的:治療群がプラセボ群よりも有意にスコア改善するかを検証。
MMRMによる解析の流れ
- モデル構築:群、時点、群×時点の交互作用を固定効果として指定
- 共分散構造の選択:非構造型(UN)を採用
- LS Meanの推定:各時点での群間差を算出
- 群×時点の交互作用の検定:治療効果の時間的推移を評価
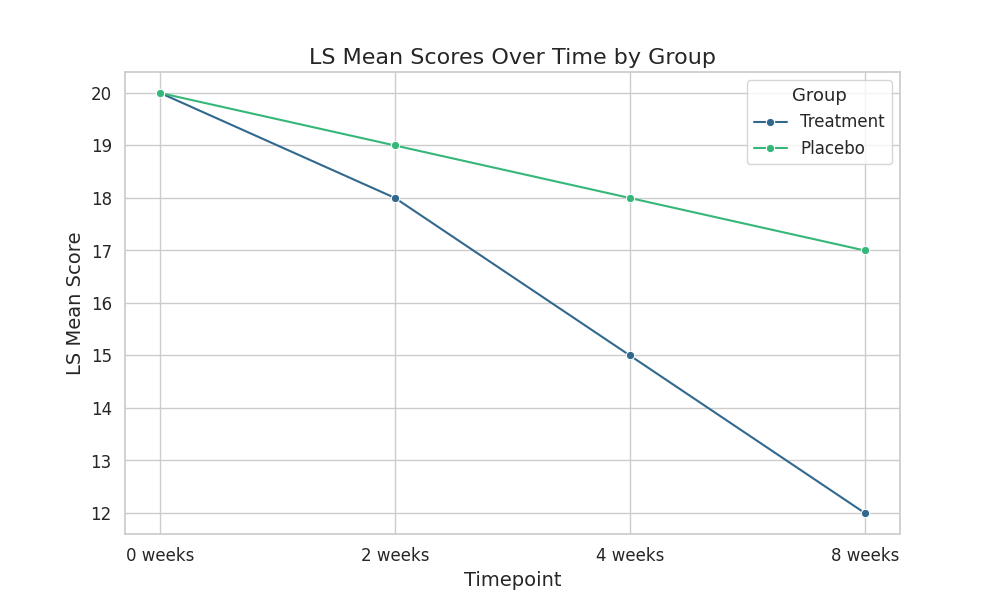
- 横軸(Timepoint):測定時点(0週、2週、4週、8週)
- 縦軸(LS Mean Score):各群の最小二乗平均スコア
- 線の色とマーカー:治療群とプラセボ群を明確に区別
この図から、治療群は時間とともにスコアが大きく改善しているのに対し、プラセボ群は緩やかな改善にとどまっていることが視覚的に把握できます。群×時点の交互作用の存在を示唆する典型的なパターンです。
MMRMが適している場面
MMRMを使うのに適している状況について解説していきます。
欠測値が多い試験:例)長期フォローアップ試験
- 例:慢性疾患の治療効果を1年、2年と追跡する試験
- 課題:フォローアップ中の脱落(欠測)が多くなる
- MMRMの強み:MAR(Missing At Random)仮定のもと、欠測値を除外せずに解析可能
ベースライン補正が不要な場合
- 方法:ベースライン値を共変量としてモデルに含める(ANCOVA的な拡張)
- 利点:ベースラインのばらつきを調整し、群間差の推定精度を向上
治療効果が時間とともに変化する場合
- 例:アルツハイマー病の認知機能スコア(ADAS-Cog)の推移をモデル化
- 目的:疾患進行の速度に対する治療効果を評価
- 利点:時系列の相関構造を明示的にモデル化できる
この他にも反復測定が不均一な間隔で行われる場合にも適していると考えられております。
注意点と限界
MMRMは一見優れた解析手法にも思えますが、注意点と解析の限界もございます。
- 解釈には統計的素養が必要:LS Meanの意味や交互作用の解釈に注意が必要です。
- MAR仮定の妥当性:欠測がランダムでない場合、バイアスが生じる可能性あります。
- モデル選択の自由度が高い:共分散構造の選択によって結果が変わることもあります。そのため、治験実施計画書や統計解析計画書で事前に規定しておくことが大切となります。
まとめ
MMRMは、臨床試験における反復測定データの解析において、柔軟性・頑健性・解釈の明快さを兼ね備えた強力な手法です。特に、欠測値の扱いや時系列の相関構造に悩む場面では、MMRMが最適な選択肢となるでしょう。
臨床研究や臨床試験において、MMRMの理解と適切な応用は、統計解析の質を大きく左右する重要なスキルとなります。