Jonckheere の順位和検定を徹底解説：順序をもつ多群比較に最適なノンパラメトリック手法

記事の目次

はじめに

Jonckheere の順位和検定（Jonckheere–Terpstra test）は、順序づけられた複数群の中央値が単調に変化しているかどうかを評価するノンパラメトリック検定です。群に自然な順序がある場合に特に有効で、Kruskal–Wallis 検定よりも高い検出力を持つことが知られています。医療統計では、用量反応関係の解析などで頻繁に利用されます。

検定の目的と背景

複数群を比較する際、群に自然な順序が存在することがあります。

低用量
中用量
高用量

このような状況では、中央値が

\[\theta _1\leq \theta _2\leq \theta _3\]

のように 単調増加しているかどうかを検証したい場面が多くあります。

Kruskal–Wallis 検定は「どこかに差があるか」を調べる検定ですが、順序に沿った増加（または減少）傾向があるかどうかは評価できません。そこで Jonckheere の順位和検定が活躍します。

検定統計量 J の考え方

Jonckheere 検定の基本アイデアは、後ろの群が前の群より大きい観測値を持つ回数（勝ち数）を数えることです。

指示関数による定義

群 i と群 j（i 群< j)について群 j の観測値 y が群 i の観測値 x より大きければ 1 点加算します。

\[J=\sum _{i<j}\sum_{x \in G_i}\sum_{y \in G_j}I(y>x)\]

後ろの群の値が前の群より大きいほど、J は大きくなります。

単調増加のイメージ

このように、群が順序に沿って右上がりに並ぶ場合、後ろの群の値が前の群より大きいことが多く、J は大きくなります。

勝ち数のカウント方法

例として、群1（低用量）と群2（中用量）を比較します。

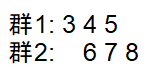
勝ち数のカウントは次のようになります。
3 < 6 → 勝ち
3 < 7 → 勝ち
3 < 8 → 勝ち

4 < 6 → 勝ち
4 < 7 → 勝ち
4 < 8 → 勝ち

5 < 6 → 勝ち
5 < 7 → 勝ち
5 < 8 → 勝ち

合計 9 勝です。
このように、群が順序に沿って大きくなるほど勝ち数が増え、J が大きくなります。

J の期待値と分散

帰無仮説 \(H_0\)：「群間に単調な傾向はない」

このとき J の期待値と分散は次のように与えられます。

\[E(J)=\frac{1}{4}\left( N^2-\sum n_i^2\right)\]

\[Var(J)=\frac{1}{72}\left( N^2(2N+3)-\sum n_i^2(2n_i+3)\right)\]]

標準化統計量は次のように計算します。

\[Z=\frac{J-E(J)}{\sqrt{Var(J)}}\]

仮説の立て方

帰無仮説 \(H_0\):群の中央値に単調な傾向はありません。

対立仮説 \(H_1\):群の中央値が単調に増加（または減少）しています。

Kruskal–Wallis 検定との違い

検定	目的	順序情報の利用
Kruskal–Wallis	群間に差があるか	使わない
Jonckheere	群間に単調な傾向があるか	使う

群に自然な順序がある場合、Jonckheere 検定の方が検出力が高くなります。

R による実装例

library(clinfun)

group <- factor(rep(1:3, each = 10))
value <- c(rnorm(10, 0), rnorm(10, 1), rnorm(10, 2))

jonckheere.test(value, group, alternative = “increasing”)

例題：用量反応関係の検証

データ例

低用量: 3, 4, 5, 6
中用量: 5, 6, 7, 8
高用量: 7, 8, 9, 10

データの並び

J の計算イメージ

低 vs 中：ほぼすべて中が勝つ
中 vs 高：ほぼすべて高が勝つ
低 vs 高：当然高が勝つ

結果として J は大きくなり、p 値は小さくなります。

利点と注意点

群に順序があるときに最適です
Kruskal–Wallis より検出力が高いです
ノンパラメトリックで頑健です

群の順序が明確である必要があります
単調性が前提であり、途中で上下するパターンには弱いです

まとめ

Jonckheere の順位和検定は、順序づけられた複数の群に対して、中央値が単調に増加または減少しているかどうかを評価するためのノンパラメトリック検定です。群間の「勝ち数」を数えるという直感的な仕組みに基づいており、群に自然な順序が存在する場合には Kruskal–Wallis 検定よりも高い検出力を発揮します。用量反応関係のように、群の順序が明確で、効果が段階的に変化すると考えられる場面で特に有用です。一方で、単調性が前提となるため、途中で増減が入り混じるようなパターンには適していません。順位データに基づくため分布の仮定に依存せず、外れ値にも頑健である点も利点です。順序をもつ多群比較を行う際には、まず候補として検討すべき検定方法だといえます。

参考書籍

医学への統計学

[商品価格に関しましては、リンクが作成された時点と現時点で情報が変更されている場合がございます。]

医学への統計学第3版（統計ライブラリー） [ 古川俊之 ]
価格：5,500円（税込、送料無料) (2026/2/11時点)

楽天で購入

Jonckheere 用量ー反応関係順位和検定