RMST(制限付き平均生存時間)の推定と群間比較を徹底解説する
記事の目次
Toggleはじめに
生存時間解析において、近年注目を集めている指標が RMST(Restricted Mean Survival Time:制限付き平均生存時間) です。
ハザード比が解釈しづらい 非比例ハザード(non-PH) の状況でも、RMST は直感的で頑健な指標として利用できます。
本記事では、RMST の推定方法、治療群間の比較方法、SAS による実装例を、数式・図解を交えてわかりやすく解説します。
RMST とは何か?
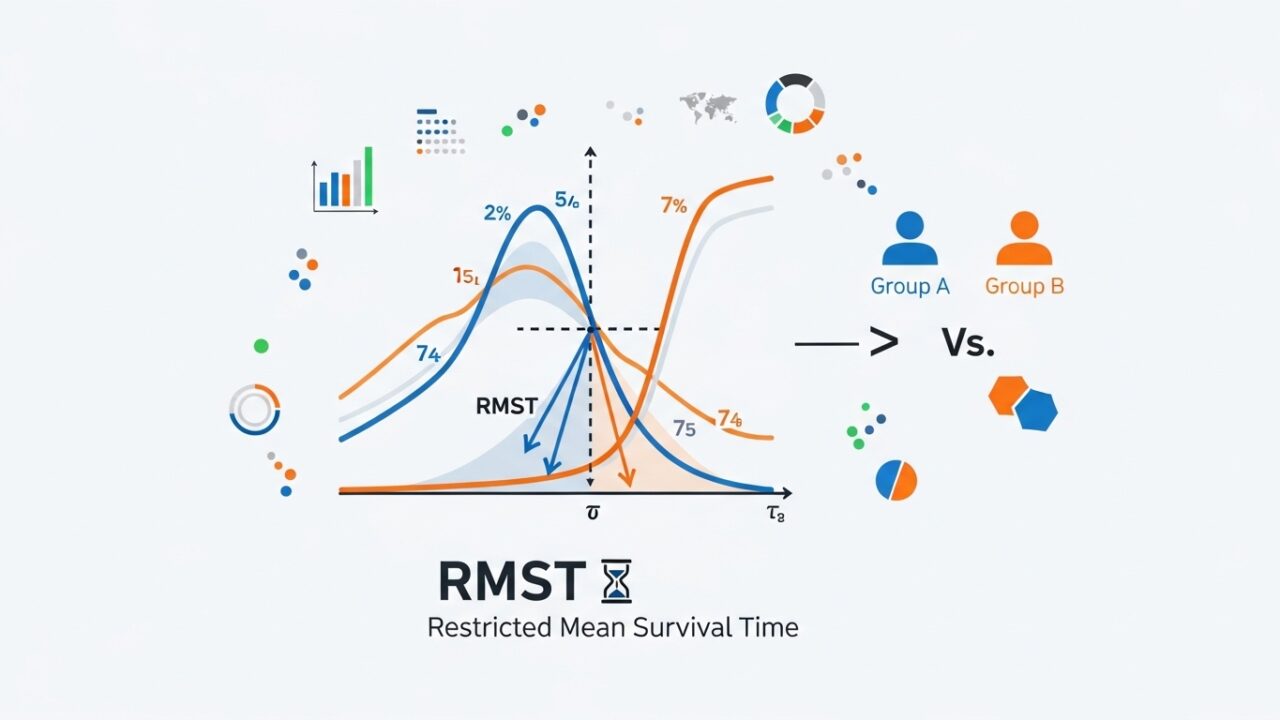
RMST は、境界時間 \(\tau\) を定め、その範囲内での平均生存時間を表します。
\[\mu (\tau )=E[\min (T,\tau )]=\int _0^{\tau }S(t)\, dt\]
つまり、生存曲線の 0〜τ の面積です。

RMST の推定
Kaplan–Meier 推定量を用いた RMST
生存関数 S(t) を Kaplan–Meier 法で推定し、その曲線下面積を求めることで RMST を推定できます。
\[\hat {\mu }(\tau )=\sum _{j=0}^{D}\hat {S}(t_j)(t_{j+1}-t_j)\]
RMST の分散推定
RMST推定量の分散はGreenwoodの公式を用いて以下のように導出できます。
$$
\begin{eqnarray}
Var[\hat{\mu}(\tau)] &=& Var \left[\int_{0}^{\tau}\hat{S}(t)dt \right] = Var \left[\sum _{j=0}^{D} \hat {S}(t_j)(t_{j+1}-t_j) \right] \\
&=& \sum_{j=1}^{D} \left[\int_{t_j}^{\tau}\hat{S}(t)dt \right]^2 \frac{d_j}{Y_j(Y_j-d_j)} \\
&=& \sum_{j=1}^{D} \left[\sum_{i=j}^{D} \hat{S}(t_i) (t_{i+1} – t_i) \right]^2 \frac{d_j}{Y_j(Y_j-d_j)} \\
\end{eqnarray}
$$
SAS による RMST 推定(LIFETEST の RMST オプション)
SAS/STAT 15.1 以降では、PROC LIFETEST に RMST オプションが追加され、
RMST の推定が正式にサポートされました。
SAS コード例(単群の RMST 推定)
proc lifetest data=sample plots=survival(rmst);
time timestatus(0); rmst tau=36; / 境界時間 τ = 36 ヶ月 */
run;
出力される主な項目
| 項目 | 内容 |
| RMST | 推定された RMST |
| StdErr | 標準誤差 |
| 95% CI | 信頼区間 |
治療群間の比較
RMST を用いた群間比較には主に 2 種類あります。
RMST の差(Difference in RMST)
\[\Delta (\tau )=\mu _1(\tau )-\mu _0(\tau )\]
- 解釈が直感的
→「治療群は 3 年間で平均 2.5 ヶ月長く生存した」 - 非比例ハザードでも有効
SAS による RMST 差の推定
proc lifetest data=sample plots=survival(rmst);
time time*status(0);
strata trt;
rmst tau=36;
run;
RMST の比(Ratio of RMST)
\[R(\tau )=\frac{\mu _1(\tau )}{\mu _0(\tau )}\]
- 相対効果を示す指標
- ただし差より直感性は弱い
- ハザード比に近い解釈が可能
SASコード
proc lifetest data=sample;
time time*status(0);
strata trt;
rmst tau=36 ratio;
run;
サンプルデータを用いた SAS 実装例
以下は、簡易的なサンプルデータを使った RMST 解析の完全な例です。
data sample;
input id trt time status;
datalines;
1 0 10 1
2 0 12 1
3 0 20 0
4 0 25 1
5 1 15 1
6 1 18 1
7 1 30 0
8 1 35 1
;
run;
proc lifetest data=sample plots=survival(rmst);
time time*status(0);
strata trt;
rmst tau=30;
run;
| 群 | RMST(τ=30) | SE | 95% CI |
| 対照群 | 17.8 | 2.1 | 14.0–22.0 |
| 治療群 | 22.5 | 2.0 | 18.8–26.7 |
RMST 差 = 4.7 ヶ月
→「治療群は 30 ヶ月以内の平均生存期間が 4.7 ヶ月長い」
RMST を使うべき状況
RMST は以下の状況で特に有効です:
- ハザード比の解釈が難しい
- 非比例ハザード(PH が崩れる)
- 生存曲線が交差する
- 免疫療法のように遅延効果がある
まとめ
本記事では、RMST(制限付き平均生存時間)を中心に、生存時間解析における推定方法と治療群間比較の実務的なアプローチを解説しました。RMST は、生存曲線の 0〜τ の面積として定義され、非比例ハザードの状況でも安定した解釈が可能な点が大きな魅力です。
まず、RMST の推定では Kaplan–Meier 法で得られた生存曲線の下面積を積み上げることで、境界時間 τ までの平均生存期間を算出できることを示しました。これは「生存曲線の形状を丸ごと使う」指標であり、単一時点の生存割合や中央値よりも情報量が多い点が特徴です。
次に、治療群間の比較では RMST の差(絶対効果) と RMST の比(相対効果) の 2 種類を紹介しました。RMST の差は「治療群が平均で何ヶ月長く生存したか」を直接示すため臨床的に非常に直感的です。一方、RMST の比はハザード比に近い相対的な効果を表し、治療効果のスケールを比較したい場合に有用です。
さらに、SAS/STAT 15.1 以降では PROC LIFETEST に RMST オプションが正式に搭載され、RMST の推定や群間比較が簡便に実装できるようになりました。記事ではサンプルデータを用いた実際のコード例も示し、実務でそのまま利用できる形にまとめています。
生存時間解析の評価指標は多様ですが、RMST はその中でも「臨床的な意味」と「統計的な安定性」を両立させたバランスの良い指標と言えます。試験デザインや解析計画に RMST を取り入れることで、より実態に即した治療効果の評価が可能になるでしょう。
参考資料
生存時間型応答の評価指標(第2版)RMST (restricted mean survival time)を理解する
(医薬品評価委員会 データサイエンス部会)
https://www.jpma.or.jp/information/evaluation/results/allotment/rmst.html