RMST による調整解析と症例数設計を徹底解説
記事の目次
Toggleはじめに
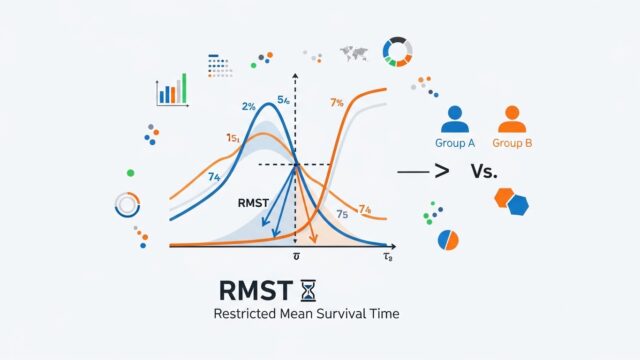
Restricted Mean Survival Time(RMST)は、比例ハザード性が成り立たない状況でも直感的かつ安定した治療効果指標を提供できる点から、近年注目が高まっています。
本記事では、「生存時間型応答の評価指標(第2版)」を参考に3.4 調整解析 と 3.5 症例数設計 を中心に、RMST を実務で使う際に必ず押さえておきたいポイントを整理します。
RMSTの基礎的な内容については以下の記事で紹介しておりますので、是非ご一読ください。
RMST の調整解析
RMST は Kaplan–Meier 推定量を積分することで得られるため、基本的には「非パラメトリックな平均生存時間の比較」という位置づけです。しかし、実際の臨床試験では 層別化因子の調整 や 共変量調整 が必要になる場面が多くあります。
RMST の調整解析として以下の 3 つが紹介されています:
- 3.4.1 層別解析
- 3.4.2 回帰分析(RMSTREG)
- 3.4.3 Cox モデルによる調整解析
順にわかりやすく解説します。
層別解析
層別解析は、治療群ごとに層別 Kaplan–Meier 曲線を推定し、層別 RMST を算出したうえで、層の重み付け平均を取る方法です。
● 層別 RMST の考え方
層 s における RMST を \(\mu _s(t)\)、層の重みを \(w_s\) とすると、層別 RMST は
\[\mu _{strat}(t)=\sum _sw_s\mu _s(t)\]
で定義されます。
重み \(w_s\) には以下がよく使われます:
- 層のイベント数比
- 層のサンプルサイズ比
RMST の回帰分析(3.4.2)
SAS では RMSTREG プロシジャが追加され、共変量調整を含む RMST 回帰が可能になりました。
● モデルの基本形
RMST を従属変数とし、治療群や共変量を説明変数とする線形回帰モデルです。
\[\mu _i(t)=\beta _0+\beta _1\cdot \mathrm{Trt_{i}}+\beta _2Z_{i1}+\cdots +\beta _pZ_{ip}\]
ここで:
- \(\mu _i(t)\):被験者 i の RMST
- \(\mathrm{Trt_{i}}\):治療群(0/1)
- \(Z_{ij}\):共変量
治療効果は \(\beta _1\) として推定されます。
- 共変量調整により推定精度が向上
- 非比例ハザードでも解釈が容易
- RMST の差を直接推定できる
- 境界時間 t の設定が必要
- モデルの線形性を仮定する
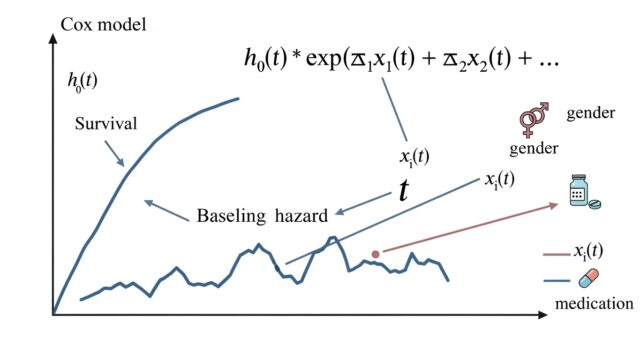
Cox モデルによる調整解析
Cox モデルはハザード比を推定するためのモデルですが、添付文書では RMST の調整解析にも利用できると説明されています。
● どう使うのか?
Cox モデルで推定した生存関数(ベースライン+共変量調整)を用いて RMST を計算します。
\[\hat {\mu }(t)=\int _0^t\hat {S}(u)\, du\]
- Cox モデルの枠組みをそのまま利用できる
- 共変量調整が容易
- RMST の利点(非比例ハザードに強い)が薄れる可能性
- 比例ハザード性が成り立たない場合、Cox モデルの推定生存関数が不安定になる
RMST の症例数設計
RMST を主要評価指標として試験を設計する場合、RMST の差の検出力を基準に症例数を決定します。
以下の構成で詳細に説明されています:
- 3.5.1 計算手順
- 3.5.2 SAS マクロの実行
- 3.5.3 指数分布を仮定した必要症例数
- 3.5.4 区分指数分布を仮定した必要症例数
- 3.5.5 境界時間と必要症例数の関係
順に整理します。
2.1 症例数計算の基本(3.5.1)
RMST の差を
\[\Delta =\mu _T(t)-\mu _C(t)\]
とします。
治療群・対照群の RMST の分散をそれぞれ
\[\sigma _T^2(t),\quad \sigma _C^2(t)\]
とすると、2 群比較の検定統計量は
\[Z=\frac{\Delta }{\sqrt{\sigma _T^2/n_T+\sigma _C^2/n_C}}\]
となります。
● 必要症例数の基本式
両側検定で有意水準 \(\alpha\) 、検出力 \(1-\beta\) を満たすための総症例数 N は
\[N=\frac{\left( z_{1-\alpha /2}+z_{1-\beta }\right) ^2\left( \sigma _T^2+\sigma _C^2\right) }{\Delta ^2}\]
(群割付比 1:1 の場合)
RMST の分散(3.1 節より)
症例数設計では RMST の分散が必要です。添付文書では次の式が示されています:
\[\mu (t)=\int _0^tS(u)\, du\]
\[\sigma ^2(t)=2\int _0^tuS(u)\, du-\mu (t)^2\]
指数分布を仮定した症例数
指数分布(ハザード \lambda )を仮定すると RMST は解析的に求まります。
次の式が示されています:
\[\mu (t)=\frac{1-e^{-\lambda t}}{\lambda }\]
\[\sigma ^2(t)=\frac{1-e^{-2\lambda t}}{\lambda ^2}-\mu (t)^2\]
これを用いて症例数を計算します。
まとめ
RMST(Restricted Mean Survival Time)は、非比例ハザードの状況でも解釈しやすい生存時間指標として注目されています。3.4 節では RMST の調整解析が整理されており、まず層別解析では層ごとに RMST を算出し、サンプルサイズなどを重みにして統合する方法が紹介されています。SAS/STAT 15.1 では LIFETEST プロシジャにより層別 RMST が正式に計算可能となり、実務での利用が容易になりました。さらに RMSTREG プロシジャを用いた回帰分析では、RMST を従属変数とした線形モデルにより共変量調整が可能となり、非比例ハザード下でも安定した治療効果推定が得られます。また Cox モデルを用いて推定生存関数を積分する方法もありますが、比例ハザード性が崩れる場合には注意が必要です。
3.5 節の症例数設計では、RMST の差と分散を用いて必要症例数を算出する枠組みが示されています。指数分布や区分指数分布を仮定することで RMST と分散を解析的に求められ、症例数計算に利用できます。特に境界時間 t の設定は症例数に大きく影響し、t を長くすると RMST の差は大きくなる一方で分散も増えるため、症例数が必ずしも減るとは限りません。治療効果が現れるタイミングを踏まえ、適切な境界時間を設定することが重要です。
参考資料
生存時間型応答の評価指標(第2版)RMST (restricted mean survival time)を理解する
(医薬品評価委員会 データサイエンス部会)
https://www.jpma.or.jp/information/evaluation/results/allotment/rmst.html