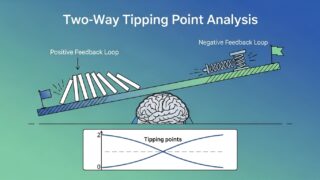
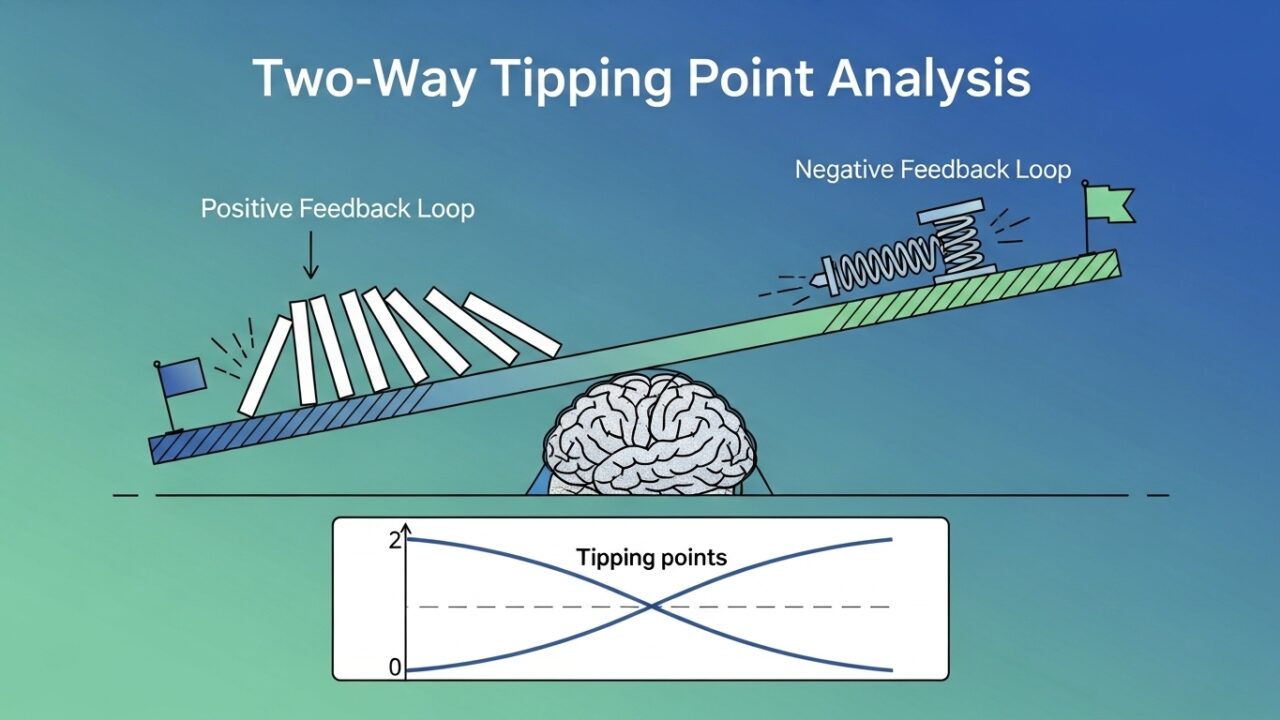
two-way Tipping Point Analysisの考え方についてやさしく解説する
記事の目次
Toggleはじめに
臨床試験では欠測値の検討は避けられません。しかし、欠測値の扱い方次第では推定結果が大きく変わる可能性があります。そこで、重要なのかティッピング解析(Tipping Point Analysis)です。
この記事では「二方向ティッピング解析(two-way Tipping Point Analysis)」をわかりやすく解説いたします。
Tipping Point Analysisとは?
欠測値に対して様々な仮定を置いたとき、推定された治療差がどの程度変化するかを感度分析
例えば、
- 治療群Pの欠測被験者は「悪化方向」に補正する。(\(\Delta_{1}\))
- 治療群Aの欠測被験者は「改善方向」に補正する。(\(\Delta_{2}\))
といった複数の補正量を振りながら、推定された治療差の変化を可視化します。
ここで、2方向とは、
- 治療群Pの補正量\(\Delta_{1}\)
- 治療群Aの補正量\(\Delta_{2}\)
の2軸で感度分析を行っていくという意味です。
モデルの前提:正規線形モデル
まず、各多重代入データセット(imputed dataset)で以下の正規線形モデルをあてはめます。
\[Y = X\beta + \varepsilon, \varepsilon \sim N(0,\sigma^2I)\]
ここで、
- Y : アウトカム(imputedを含む)
- X : 説明変数(治療差、ベースライン調整、層別因子等)
- \(\beta\) : 固定効果パラメータ
多重代入を行っても、Xは全データセット共通なので
\[\hat{\beta} = (X’X)^{-1}X’Y\]
の構造は変わりません。
治療差はYの線形和として書ける
治療差の推定値っを\(b_{dif}\)とすると、
\[b_{dif} = \sum_{i \in P}c_iy_i + \sum_{j \in A}d_iy_i\]
のようにYの線形結合になります。
欠測値\(\Delta_{1}\),\(\Delta_{2}\)で調整すると治療差はどう変わる?
欠測値のみを補正し、
- 治療群Pの欠測値→\(y_i + \Delta_{1}\)
- 治療群Aの欠測値→\(y_j + \Delta_{2}\)
とすると、補正後の治療差\(b_{tip}\)は
\[b_tip= b_dif +\Delta_1 \sum_{i \in P,I}c_i + \Delta_2 \sum_{j \in A,I}d_i\]
つまり、治療差は\(\Delta_{1},\Delta_{2}\)の一次関数になる。
Within-imputationの残差平方和も\(\Delta_{1}\),\(\Delta_{2}\)の二次式になる
RSSは
\[R^{2}=Y'(I – X(X’X)^{-1}X’)Y=Y’ \Omega Y\]
と書けます。
補正後は
\[R^{2}_{tip}=(Y+\Delta_1R_p+\Delta_2R_A)’\Omega (Y+\Delta_1R_p + \Delta_2 R_A)\]
展開すると
\[R^{2}_{tip}=Y’ \Omega Y + 2Y’ \Omega (\Delta_1R_p + \Delta_2 R_A) + \Delta_{1}^{2}R’_{P}\Omega R_{P} + \Delta_{2}^{2}R’_{A}\Omega R_{A} + 2\Delta_1 \Delta_2 R’_{P} \Omega R_A \]
つまり、RSSは\(\Delta_1, \Delta_2\)の2次式になります。この性質が後の推定式構築を可能にします。
Rubinのルールでのポイント
多重代入ではRubinのルールにより、
- 治療差のbetween variance (VB)
- within variance (VW)
を足し合わせて標準誤差を求めます。
VB(between variance)は\(\Delta_1, \Delta_2\)を変えても、不変である。
X行列が一定なので、欠測値の変動(多重代入による違い)は治療差の変更に線形的に作用し、\(\Delta\)による追加成分は全データセットで同じためです。
一方、VV(within variance)はRSSに依存するため、\(\Delta_1, \Delta_2\)によって変化し、二次式で表現されます。
具体的な手順
Step1:N個の多重代入データセットを作成(Rubinサンプル)
MI(Multiple imputation)を実施し、N個のデータセットを作成します。
step2:5組の(\(\Delta_1, \Delta_2\))ペアを設定
例:
| パターン | \(\Delta_1\) | \(\Delta_2\) |
| 1 | -2 | -2 |
| 2 | -2 | +2 |
| 3 | +2 | -2 |
| 4 | +2 | +2 |
| 5 | 0 | 0 |
これら5組をすべてのMIデータに適用し、「5つの追加のRubinサンプル」を作ります。
Step3:各Rubinサンプルを通常の線形モデルで解析し、Rubinのルールで統合
ここから、
- 治療差の推定値
- Within variance(VW)
- Between variance(VB)
step4:治療差を\(\Delta_1, \Delta_2\)の一次式としてfitting
6点分の治療差がわかるので、以下の一次式の係数が求まります。
\[b_tip = \alpha_0 + \alpha_1 \Delta_1 + \alpha_2 \Delta_2\]
step5:VWを\(\Delta_1, \Delta_2\)の二次式として推定
\[VW(\Delta_1, \Delta_2) = \beta_0 + \beta_1 \Delta_1 + \beta_2 \Delta_2 + \beta_3 \Delta_{1}^{2} + \beta_4 \Delta_{2}^{2} + \beta_5 \Delta_1 \Delta_2 \]
これを6点のデータから推定します。
step6:任意の(\(\Delta_1, \Delta_2\))に対して治療差・SE・p値を推定
ここまでで得られた回帰式から、
- 推定治療差
- 推定標準誤差
- t値、p値
を任意の\(\Delta_1, \Delta_2\)で計算できます。
まとめ
two-way Tipping Point Analysisは多重代入(MI)で欠測値を補完した後に「欠測だった値が本当はどの程度よかったか/悪かった可能性があるか」という仮定を治療群ごとに別々で動かし、結論の頑健性を二次元で可視化する感度分析です。申請などでこの解析を行うことで、結果の信頼性をより増すことができるようになりますので、理論から実装までを理解するための一助となりますと幸いです。